Методы расчёта и исследования магнитных полей можно подразделить на три группы: аналитическую, графическую и экспериментальную.
Группу аналитических методов объединяют все чисто аналитического порядка приёмы интегрирования уравнения Пуассона (для областей, занятых током), уравнения Лапласа (для областей, не занятых током), применение метода зеркальных отображений (широко используется для расчёта магнитных полей, создаваемых линейными токами, протекающими вблизи стальных масс) и другое.
В силу трудностей математического характера классические аналитические методы позволяют решать относительно небольшой круг задач.
В тех случаях, когда расчёт поля аналитическими методами вызывает затруднения, прибегают к графическому методу построения картины поля или к исследованию магнитного поля на модели. Графические методы построения картины поля применимы к двухмерным безвихревым полям.
За последние годы применяют также метод интегральных уравнений, предполагающий использование ЭВМ и значительно расширяющий круг решаемых задач.
Опытное исследование картины магнитного поля производят различными методами. Один из них основан на явлении электромагнитной индукции и состоит в следующем. Плоскую очень малых размеров рамку с намотанной на неё обмоткой помещают в исследуемую область поля и соединяют с баллистическим гальванометром. При быстром удалении рамки в область, где магнитное поле заведомо слабое, измеряют количество электричества, протекшее по баллистическому гальванометру, и по нему судят о среднем значении индукции в рамке. Затем рамку помещают в другую точку поля и снова определяют индукцию и так далее. Этот метод даёт возможность исследовать магнитные поля практически любой конфигурации в пространстве вне ферромагнетиков.
|
|
Качественное исследование магнитного поля часто производят с помощью стальных опилок, которые насыпают на плоский лист из неферромагнитного материала, помещают в магнитное поле и слегка по листу постукивают. Опилки расположатся вдоль силовых линий. По густоте силовых линий можно качественно судить об интенсивности магнитного поля.
Вместо опилок нередко используют мельчайшие порошки окислов железа, находящихся во взвешенном состоянии в какой - либо жидкости, например керосине.
Так как в рассматриваемой задаче во всех трёх областях (внутренняя область, область тела экрана, область снаружи экрана) нет тока, то решение задачи сводится к интегрированию уравнения Лапласа 
.
Выбрав систему координат таким образом, чтобы граничные поверхности в поле описывались наиболее удобно и соответствующим образом раскрыв уравнение Лапласа, получим уравнение в частных производных
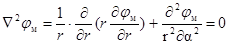, (5)
для интегрирования которого можно применить метод Фурье. Тогда, согласно этому методу, искомую функцию полагают в виде произведения двух пока неизвестных функций M и N, одна из которых зависит только от r, а вторая - от α
. (6)
Вид функций M и N подлежит определению. Определение функции φ в виде произведения двух функций (6) позволяет разбить уравнение в частных производных (5) на два обыкновенных дифференциальных уравнения, из которых одно будет составлено относительно M, другое - относительно N.
Для расчета и анализа магнитных экранов может быть использован модуль магнитостатика, который имеется в мощном современном комплексе программ для инженерного моделирования электромагнитных, тепловых и механических задач методом конечных элементов, носящем название ELCUT.
|
|
Решение задачи в ELCUT начинается с выбора формулировки. Нелинейная задача магнитостатики записана относительно векторного магнитного потенциала.
Для работы с двумерной моделью в ELCUT имеется редактор геометрической модели. Он оснащен небольшим, но тщательно отобранным набором инструментов.
Закончив рисование модели, следует приступать к построению сетки. Все процедуры метода скрыты в недрах программы и не требуют никакого вмешательства. К примеру, построение сетки треугольных конечных элементов может быть выполнено одним щелчком мыши. Такая автоматическая сетка всегда пригодна для начального прикидочного расчета, а во многих случаях подходит и для окончательного решения. Если этого недостаточно - можно сгустить или разредить сетку в нужных местах, указав желаемый пространственный шаг на любом наборе вершин. Генератор сетки работает в два этапа. Сначала подобласти (в терминологии ELCUT - блоки) разрезаются на подблоки. При этом преследуются две цели: ликвидация геометрической многосвязности и оптимизация размера областей с точки зрения процесса решения.
Для задания источников поля и граничных условий в редакторе модели нужно пометить геометрические объекты, которые понадобятся в дальнейшем, текстовыми метками (желательно мнемоническими). В дальнейшем для каждой метки можно задать свойства материала, значения источников поля, граничные условия разных видов и прочее. При этом физические свойства хранятся отдельно от геометрических данных, что облегчает многовариантные расчеты.
|
|
В магнитных задачах источниками поля являются токи (объемные, поверхностные или линейные) и постоянные магниты. Магнитные свойства материалов могут быть заданы кривой намагничивания или константой. В последнем случае допустима анизотропия свойств.
Источники и граничные условия полностью независимы от сетки и могут быть изменены в любое время.
На внешних и внутренних ребрах могут быть поставлены граничные условия следующих типов: заданный потенциал (условие Дирихле), заданная плотность потока (условие Неймана) и специальный вид условия Дирихле, при котором потенциал заданной поверхности постоянен, но заранее неизвестен. В магнитной задаче такое условие моделирует сверхпроводник.
Сильной стороной ELCUT является необычно высокая скорость решения задачи. Она достигается применением фирменной технологии "метод геометрической декомпозиции". С точки зрения решения разреженной системы линейных алгебраических уравнений это вариант метода сопряженных градиентов с предобуславливанием матрицы. Технология хранения матрицы и ее обращения основана на декомпозиции области расчета на подблоки заранее оцененного оптимального размера, которая выполняется еще на этапе построения сетки.
Основные виды анализа результатов решения в пакете ELCUT состоят в следующем:
рисование картины поля различными способами;
просмотр локальных значений поля "пробником";
рисование графиков полевых характеристик вдоль заданного контура;
вычисление интегральных величин по контуру и по объему;
вычисление индуктивности, емкости и импеданса обмоток с помощью мастера;
экспорт значений поля в другие программы вдоль контура и по площади с заданным шагом;
вывод картинок в файл и на печать.
Для рисования картины поля применяются цветная заливка, изолинии потенциала (температуры), изображение векторных величин с помощью семейства направленных отрезков.
Рядом с картиной поля можно увидеть панель "полевого калькулятора", в котором сведены локальные и интегральные значения, а также электротехнические параметры, вычисляемые с помощью мастера.
Инструмент рисования контуров позволяет задать разомкнутый или замкнутый контур, состоящий из отрезков и дуг окружностей. Этот контур используется для построения графиков, табулирования физических величин и вычисления интегралов. Интегральный калькулятор позволяет вычислять силу и момент, действующий на тела, погруженные в поле, потокосцепления, магнитодвижущую силу, тепловой поток, силу и момент реакции опоры, заряд проводника и множество других величин, важных для инженера - расчетчика.
Чаще всего ELCUT применяется для расчета вращающего момента, потерь мощности и других характеристик электрических двигателей, электрической прочности изоляционных конструкций - например, кабельных вводов, индуктивности, емкости, волнового сопротивления и затухания линий передачи, электрических и тепловых параметров установок индукционного нагрева, механической прочности катушек, создающих сильное магнитное поле [9].
РАСЧЁТНАЯ ЧАСТЬ
магнитный экран фурье лаплас
В равномерном магнитном поле надо заэкранировать сферическую область пространства. В данной курсовой работе требуется доказать, что в результате применения стального магнитного экрана, внутренний диаметр равен 40 мм, внешнее поле 
ослабляется в 300 раз, то есть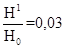 
(
- напряжённость поля внутри экрана).
Рисунок 3 - Сферический магнитный экран
Сферический экран внутренним радиусом a = 100 мм, наружным b = 170 мм имеет относительную магнитную проницаемость 
= 600 (рисунок 3). Внутреннюю область обозначим 1, область тела экрана - 2, область снаружи экрана - 3.
Так как во всех трёх областях нет тока, то магнитное поле в них описывается уравнением Лапласа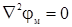 
.
В рассматриваемой задаче граничная поверхность наиболее удобно описывается в сферической системе координат. Поэтому будем пользоваться этой системой.
Экран будем полагать достаточно протяжённым вдоль оси z (ось z перпендикулярна чертежу); 
зависит только от координат r и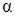 
цилиндрической системы. Раскрыв уравнение Лапласа в цилиндрической системе, получим уравнение (5), которое представляет собой уравнение в частных производных. Для интегрирования (5) применим метод Фурье. Искомую функцию будем полагать в виде произведения двух функций M и N, одна из которых зависит только от r, а вторая - от α (6).
Разобьём уравнение в частных производных (5) на два обыкновенных дифференциальных уравнения, из которых одно будет составлено относительно M, другое - относительно N.
Подставим (6) в (5), учтя, что
, 
. (7)
Поэтому
. (8)
Умножим (8) на 
. (9)
Первое слагаемое в уравнении (9) представляет собой функцию только r, а второе - функцию α. Сума двух функций, из которых одна зависит только от r, а другая - от α, равна нулю для бесчисленного множества пар значений r и α (уравнение (9) подходит для всех точек поля). Это возможно только тогда, когда каждая из данных функций равна нулю
, (10)
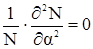, (11)
либо когда
, (12)
, (13)
где p - некоторое число.
Общее решение для φ, согласно (6), равно произведению решений уравнений (10), (11) плюс произведение решений для M и N по уравнениям (12), (13).
Так как в (10), (11) M зависит только от r, а N - только от α, то от частных производных можно перейти к простым
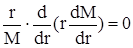, (14)
. (15)
Интеграл уравнения (14)
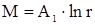. (16)
Найдём интеграл уравнения (15)
. (17)
А1 обязательно должно быть равно нулю, так как только в этом случае в решении будет отсутствовать слагаемое 
.
Потенциал есть функция непрерывная и на конечном отрезке он не может измениться на бесконечно большую величину. Из физических соображений ясно, что потенциал точек оси z не может быть равен бесконечности. Между тем, если бы 
, то в решении для потенциала присутствовало бы слагаемое , равное - ∞ для всех точек, у которых r= 0.
Найдём решение уравнений (12), (13)
(18)
или 
. (19)
Применим подстановку Эйлера
, (20)
тогда 
, (21)
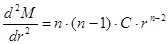. (22)
Подставим производные в уравнение (19)
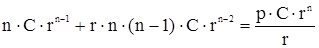(23)
или 
. (24)
Найдём корни квадратного уравнения
. (25)
Значение p определим при интегрировании уравнения
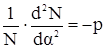. (26)
Его решение можно записать в виде
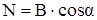. (27)
Убедимся в этом путём подстановки и одновременно найдём значение p:
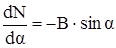; (28)
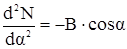; (29)
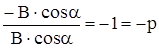. (30)
Следовательно, p = 1.
Подставим значение числа p в (25) и найдём 
.
Таким образом, полное решение запишется в виде
. (31)
Тогда можно записать:
для первой области
; (32)
для второй области
; (33)
- для третьей области
. (34)
Постоянная интегрирования, с точностью до которой определяется потенциал, принята равной нулю.
Для определения шести постоянных (
, 
, 
, 
, 
, 
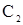) составим шесть уравнений:
) сопоставим 
с выражением “на бесконечности”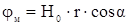 
. Из сопоставления находим, что 
;
) в первой области при r = 0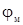 
должен оставаться конечным. Это может быть только в том случае, если в выражении будет отсутствовать слагаемое 
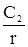. Оно будет отсутствовать при 
;
) равенство 
и 
при 
даёт уравнение
; (35)
4) равенство 
на границе между второй и третьей (при r = b) областями приводит к уравнению
; (36)
) равенство нормальных составляющих индукции
(37)
на границе между первой и второй областями (при 
)
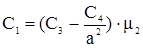; (38)
) равенство нормальных составляющих индукции при r = b даёт уравнение
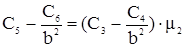. (39)
Совместное решение всех уравнений приводит к выражению потенциала в первой области
. (40)
Или при переходе к декартовой системе координат (ось x направлена вверх,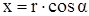 
)
. (41)
Здесь 
, (42)
, (43)
. (44)
Напряжённость поля в первой области (по модулю)
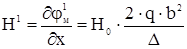. (45)
Отношение напряжённости поля внутри экрана к напряжённости внешнего поля 
(46)
или 
. (47)
Подставив числовые значения, получим
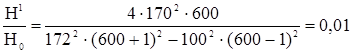
то есть напряжённость поля внутри экрана составляет 1% от напряжённости внешнего поля.
Для наглядного представления действия рассчитываемого экрана воспользуемся программным комплексом ELCUT.
Рисунок 4 - Действие магнитного сферического экрана
Как видно из рисунка, линии магнитной индукции внешнего поля, стремясь пройти по пути с наименьшим магнитным сопротивлением, сгущаются внутри стенок экрана, почти не проникая в его полость.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе был рассчитан стальной сферический магнитный экран, доказана его способность уменьшать внешнее поле в 300 раз.
Расчёты проводились аналитически с применением метода Фурье для интегрирования уравнения Лапласа. Для подтверждения полученных результатов был использован ELCUT, который позволил в течение пятнадцатиминутного сеанса на персональном компьютере, не прибегая к помощи больших ЭВМ или рабочих станций, описать задачу - её геометрию, свойства сред, источники поля, граничные и другие условия, решить её с большой точностью и проанализировать решение с помощью средств цветной графики.
ELCUT очень удобен для использования в учебном процессе, а также в производственной и исследовательской деятельности инженера - электрика при решении научных и практических задач, так как начать работу с ELCUT можно практически сразу, не отвлекаясь на изучение математических основ вычислительных алгоритмов и особенностей их реализации, редактор модели позволяет легко и быстро описать геометрию модели, при построении сетки конечных элементов можно использовать удобные средства управления ее густотой или полностью довериться автоматической системе построения сетки, кроме того, источники и граничные условия полностью независимы от сетки, и могут быть изменены в любое время.