Предмет аналитической геометрии - это изучение геометрических образов с помощью алгебры (их положение, вид, а не размеры). Точка – исходный элемент, все остальное – совокупность точек.
ЛИНЕЙНЫЕ ОБРАЗЫВ R2
Понятие об уравнении линии на плоскости.
Рассмотрим прямоугольную систему координат на плоскости, определяемую ортонормированным базисом 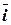 ,
, 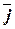 и точкой
и точкой 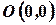 – началом координат. Пусть на плоскости дана какая-нибудь линяя.
– началом координат. Пусть на плоскости дана какая-нибудь линяя.
Определение 1. Уравнением данной линии (в выбранной системе координат) называется такое уравнение
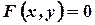
с двумя переменными, которому удовлетворяют координаты 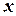 и
и 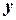 каждой точки, лежащей на этой линии, и не удовлетворяют координаты никакой точки, не лежащей на ней.
каждой точки, лежащей на этой линии, и не удовлетворяют координаты никакой точки, не лежащей на ней.
Пример. 1) 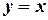 или
или  уравнение биссектрисы
уравнение биссектрисы 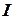 и
и  координатных углов (рис. 1).
координатных углов (рис. 1).
2) Уравнение окружности с центром в начале координат радиуса 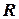 (рис. 2.):
(рис. 2.):
 |
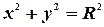 или
или  .
.
Произвольную точку на линии называют текущей точкой. В дальнейшем, рассматривая уравнения с двумя переменными, мы не исключаем возможности, что левая часть уравнения содержит еще и другие символы: 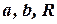 и т.д., но в таком случае мы будем предполагать, что они представляют собой фиксированные числа, и будем называть их постоянными параметрами уравнения. Например, в уравнении:
и т.д., но в таком случае мы будем предполагать, что они представляют собой фиксированные числа, и будем называть их постоянными параметрами уравнения. Например, в уравнении:
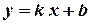
параметрами являются 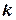 и
и  , а в уравнении окружности:
, а в уравнении окружности:
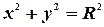
параметр - радиус 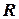 и координаты центра
и координаты центра 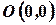 .
.
Составить уравнение линии (или, вообще говоря, геометрического образа), значит, исходя из свойств линии, установить зависимость между координатами текущей точки и параметрами. Этот метод позволяет свести изучение линий к изучению их уравнений, т.е. задачи геометрии свести к задачам алгебры.
Основным предметом изучения в аналитической геометрии являются линии, определяемые по отношению к декартовым прямоугольным координатам алгебраическими уравнениями. Это суть уравнения следующих видов:
 (1)
(1)
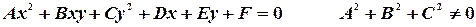 (2)
(2)
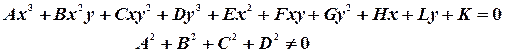 (3)
(3)
Уравнения (1), (2), (3) соответственно общие уравнения 1-ой, 2-ой, 3-ей степени.
Определение 2. Линия, которая в некоторой системе декартовых прямоугольных координат определяется алгебраическим уравнением степени  , называется алгебраической линией
, называется алгебраической линией  порядка.
порядка.
Прямая линия на плоскости
Вектор  - перпендикулярный прямой, назовем нормальным вектором прямой, а вектор
- перпендикулярный прямой, назовем нормальным вектором прямой, а вектор  , параллельный прямой, назовем направляющим вектором (рис. 3.). Пусть
, параллельный прямой, назовем направляющим вектором (рис. 3.). Пусть 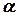 - угол между прямой и положительным направлением оси
- угол между прямой и положительным направлением оси 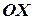 , угол наклона прямой,
, угол наклона прямой, 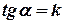 - угловой коэффициент прямой.
- угловой коэффициент прямой.
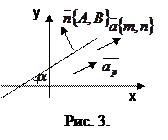 Вектор
Вектор 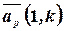 назовем приведенным направляющим вектором.
назовем приведенным направляющим вектором.
Типы уравнений прямой.
Название уравнения определяется названием постоянных величин, определяющих положение прямой линии в системе координат.
1) Уравнение прямой линии, проходящей через данную точку  , перпендикулярно данному вектору
, перпендикулярно данному вектору  имеет вид:
имеет вид:
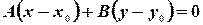 (1)
(1)
Оно вытекает из условия того, что скалярное произведение взаимно перпендикулярных векторов равно нулю.
Действительно, возьмем на прямой произвольную точку  . Образуем текущий вектор
. Образуем текущий вектор 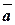 , направленный из точки
, направленный из точки  в точку
в точку  . Этот вектор будет иметь координаты
. Этот вектор будет иметь координаты  , и направлен он будет вдоль прямой. Второй вектор – это данный вектор
, и направлен он будет вдоль прямой. Второй вектор – это данный вектор  . Скалярное произведение этих векторов равно нулю, отсюда и вытекает уравнение прямой.
. Скалярное произведение этих векторов равно нулю, отсюда и вытекает уравнение прямой.
2) Общее уравнение прямой линии:
 (2)
(2)
где коэффициенты при неизвестных 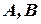 суть координаты нормального вектора прямой. Действительно, раскроем скобки в предыдущем уравнении:
суть координаты нормального вектора прямой. Действительно, раскроем скобки в предыдущем уравнении:
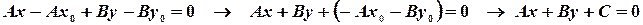
Теорема 1. Всякая прямая на плоскости имеет уравнение первой степени, и всякое уравнение первой степени является уравнением некоторой прямой.
Следствия.
a) 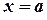 – уравнение прямой, параллельной оси
– уравнение прямой, параллельной оси 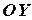 (
(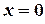 , уравнение оси
, уравнение оси 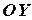 ),
),
б) 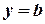 - уравнение прямой, параллельной оси
- уравнение прямой, параллельной оси 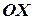 (
(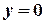 , уравнение оси
, уравнение оси 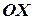 ),
),
в) 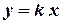 - прямая линия, проходящая через начало координат.
- прямая линия, проходящая через начало координат.
Замечание. При переменном коэффициенте 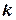 - это будут уравнения пучка прямых, проходящих через начало координат.
- это будут уравнения пучка прямых, проходящих через начало координат.
3) Уравнение прямой линии, проходящей через данную точку  , параллельно данному вектору
, параллельно данному вектору  (каноническое):
(каноническое):
 (3)
(3)
Вектор вдоль прямой  коллинеарен вектору
коллинеарен вектору  , отсюда это условие.
, отсюда это условие.
4) Уравнение прямой, проходящей через данную точку в заданном направлении:
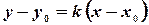 (4)
(4)
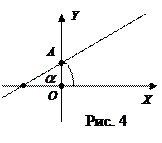 Замечание. При переменном коэффициенте
Замечание. При переменном коэффициенте 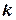 уравнение называется уравнением пучка прямых линий, проходящих через точку
уравнение называется уравнением пучка прямых линий, проходящих через точку  .
.
5) Уравнение прямой линии с угловым коэффициентом (рис. 4):
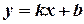 (5)
(5)
Здесь 
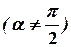 . К этому виду нельзя привести прямую, параллельную оси
. К этому виду нельзя привести прямую, параллельную оси 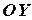 .
.
6) Уравнение прямой, проходящей через две данные точки:
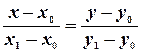 (6)
(6)
Действительно, пусть даны две точки  и
и 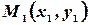 , через которые должна пройти наша прямая. На этой прямой возьмем текущую точку
, через которые должна пройти наша прямая. На этой прямой возьмем текущую точку  и образуем два вектора:
и образуем два вектора:  и
и 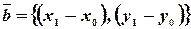 . Эти два вектора коллинеарные, отсюда и вытекает уравнение.
. Эти два вектора коллинеарные, отсюда и вытекает уравнение.
Замечание. Если 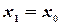 , то уравнение прямой
, то уравнение прямой 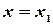 ; если
; если 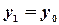 , то
, то 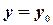 .
.
Угол между двумя прямыми. Условие параллельности и перпендикулярности.
1) Пусть прямые линии заданы общими уравнениями:
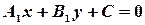
 ,
,
где нормальные векторы:  и
и 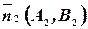 2,
2, 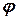 - угол между векторами
- угол между векторами 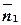 и
и  , т.е. угол между прямыми. Тогда:
, т.е. угол между прямыми. Тогда:
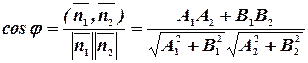 (7)
(7)
Условие параллельности прямых эквивалентно условию коллинеарности их нормальных векторов:
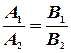 (8)
(8)
Условие перпендикулярности прямых – ортогональность векторов 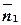 и
и  :
:
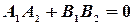 (9)
(9)
 2) Пусть прямые линии заданы с угловыми коэффициентами
2) Пусть прямые линии заданы с угловыми коэффициентами 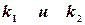 (рис. 5):
(рис. 5): 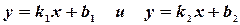 ,
,
где 
 . Тогда
. Тогда
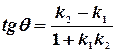 .
.
Это вытекает из формулы тангенса суммы углов. 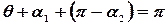 ,
, 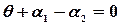 ,
, 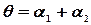 ,
, 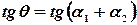 ,
, 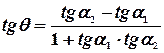 (*).
(*).
За 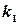 принимаем угловой коэффициент той прямой, которую надо вращать против хода часовой стрелки, чтобы обойти угол
принимаем угловой коэффициент той прямой, которую надо вращать против хода часовой стрелки, чтобы обойти угол 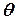 до совмещения со второй прямой.
до совмещения со второй прямой.
Условие параллельности прямых: 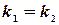 .
.
Условие перпендикулярности прямых:  .
.
Расстояние точки 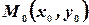 от прямой
от прямой 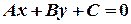 определяется формулой:
определяется формулой:
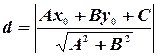 (10)
(10)
Доказательство смотри в другом файле.
Замечания.
1. Если две прямые  и
и  заданы в каноническом виде, то угол между ними можно рассматривать как угол между их направляющими векторами
заданы в каноническом виде, то угол между ними можно рассматривать как угол между их направляющими векторами 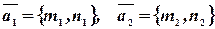 , а значит,
, а значит,
 (11)
(11)
Пример 1. Даны точки  ,
, 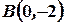 ,
,  .
.
Найти:
1) Уравнение прямой  .
.
Согласно уравнению (6) (уравнение прямой, проходящей через две точки), запишем:
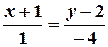 , или
, или  .
.
2) Уравнение прямой  , проходящей через точку
, проходящей через точку 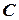 , параллельно прямой
, параллельно прямой 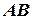 .
.
Согласно уравнению (1), (уравнение прямой, проходящей через точку параллельно данному вектору) точка 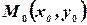 это точка
это точка 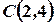 , параллельно прямой
, параллельно прямой  значит перпендикулярно ее нормальному вектору
значит перпендикулярно ее нормальному вектору 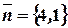 . Следовательно, запишем
. Следовательно, запишем
 .
.
3) Уравнение прямой  , проходящей через точку
, проходящей через точку 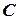 , перпендикулярно прямой
, перпендикулярно прямой  .
.
Перпендикулярно прямой, значит параллельно ее нормальному вектору, в нашем случае 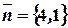 . Точка
. Точка 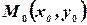 это точка
это точка  . Согласно уравнению (3), запишем
. Согласно уравнению (3), запишем
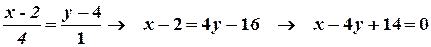
4) Уравнение медианы  треугольника
треугольника 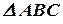 .
.
На медиане  образуем текущий вектор
образуем текущий вектор 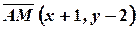 .
.
Найдем координаты точки 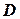 - середины стороны
- середины стороны  :
:

Образуем вектор 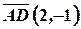 , расположенный параллельно текущему вектору
, расположенный параллельно текущему вектору 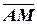 . Тогда, в силу условия параллельности векторов, получим уравнение медианы
. Тогда, в силу условия параллельности векторов, получим уравнение медианы  :
:
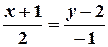 , или
, или  .
.
5) Уравнение высоты 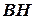 .
.
На высоте 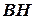 возьмем текущую точку
возьмем текущую точку 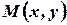 и образуем текущий вектор
и образуем текущий вектор 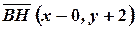 . Так как
. Так как 
 , где
, где  , то условие перпендикулярности этих векторов порождает уравнение прямой
, то условие перпендикулярности этих векторов порождает уравнение прямой 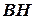 (скалярное произведение векторов равно нулю):
(скалярное произведение векторов равно нулю):
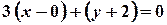 или
или 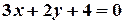 .
.
6) Длину высоты 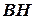 .
.
Заметим, что длина высоты 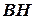 равна расстоянию от точки
равна расстоянию от точки 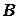 до прямой
до прямой 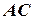 . Чтобы воспользоваться формулой (10), сначала найдем уравнение прямой
. Чтобы воспользоваться формулой (10), сначала найдем уравнение прямой 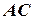 .
.
На стороне  образуем текущий вектор
образуем текущий вектор 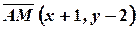 .
.
Запишем условие параллельности векторов 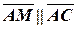 , где
, где  :
:
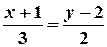 , или в общем виде
, или в общем виде 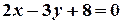 .
.
Теперь, подставляя известные данные в формулу (10), имеем:
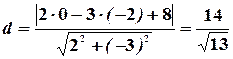 .
.
Пример 2. Дана прямая  :
: 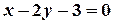 и точка
и точка 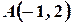 .
.
Найти:
1) Для прямой  уравнение с угловым коэффициентом, угловой коэффициент
уравнение с угловым коэффициентом, угловой коэффициент 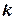 , отрезок, отсекаемый по оси ординат.
, отрезок, отсекаемый по оси ординат.
Разрешив уравнение прямой  относительно
относительно  , получаем уравнение с угловым коэффициентом:
, получаем уравнение с угловым коэффициентом:
 :
: 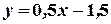 . Отсюда
. Отсюда  ,
, 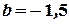 .
.
2) Нормаль 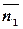 и направляющий вектор
и направляющий вектор 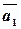 прямой
прямой  -
-  .
.
Коэффициенты при переменных 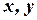 в общем уравнении прямой
в общем уравнении прямой  , есть координаты нормального вектора, то есть
, есть координаты нормального вектора, то есть 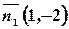 .
.
Поскольку направляющий вектор 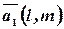 прямой
прямой  – это любой ненулевой вектор, параллельный этой прямой, то выполняется условие (перпендикулярность векторов):
– это любой ненулевой вектор, параллельный этой прямой, то выполняется условие (перпендикулярность векторов):
 где
где  .
.
Дадим величине 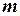 какое-нибудь значение. Пусть, например,
какое-нибудь значение. Пусть, например, 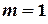 , тогда
, тогда 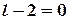 , то есть
, то есть 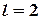 . Получаем направляющий вектор
. Получаем направляющий вектор 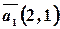 .
.
3) Каноническое уравнение прямой  .
.
Для составления канонического уравнения (3) прямой  нам необходимо знать точку
нам необходимо знать точку 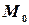 , лежащую на
, лежащую на  , и направляющий вектор
, и направляющий вектор 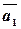 . Так как координаты вектора
. Так как координаты вектора 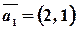 были получены нами ранее в задание 2, осталось найти координаты точки
были получены нами ранее в задание 2, осталось найти координаты точки 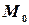 .
.
Зафиксируем произвольное значение, например,  и подставим его в уравнение прямой
и подставим его в уравнение прямой  . Получим
. Получим  . Следовательно,
. Следовательно, 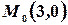 .
.
Воспользовавшись теперь каноническим уравнением прямой (10), находим:
 .
.
4) Уравнение прямой  , параллельной
, параллельной  -
- 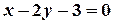 и проходящей через точку
и проходящей через точку 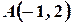 .
.
Прежде всего, заметим, что точка  не лежит на прямой
не лежит на прямой  , поскольку ее координаты не удовлетворяют уравнению этой прямой. Поэтому можно построить прямую
, поскольку ее координаты не удовлетворяют уравнению этой прямой. Поэтому можно построить прямую  , проходящую через
, проходящую через  параллельно
параллельно  , но не совпадающую с
, но не совпадающую с  .
.
Пусть 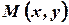 - текущая точка прямой
- текущая точка прямой  . Так как текущий вектор
. Так как текущий вектор 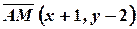 перпендикулярен вектору нормали
перпендикулярен вектору нормали 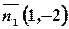 прямой
прямой  , то
, то 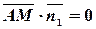 . Отсюда получаем уравнение прямой
. Отсюда получаем уравнение прямой  :
:
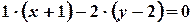 или
или 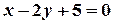
5) уравнение прямой 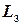 , перпендикулярной
, перпендикулярной  -
- 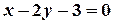 и проходящей через точку
и проходящей через точку 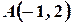 .
.
Пусть 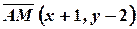 - текущий вектор прямой
- текущий вектор прямой 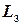 . Из условия параллельности
. Из условия параллельности 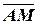 и нормали
и нормали 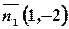 прямой
прямой  , получаем уравнение
, получаем уравнение 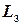 :
:
 .
.
Пример 3. Проверить, являются ли прямые линии
 ,
, 
a) Параллельными.
Прямые  и
и 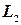 будут параллельны, если их нормали
будут параллельны, если их нормали 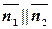 . Из общего уравнения прямой
. Из общего уравнения прямой  найдем нормаль
найдем нормаль  . Чтобы найти нормаль
. Чтобы найти нормаль  2 приведем уравнение прямой
2 приведем уравнение прямой 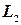 к общему виду:
к общему виду: 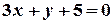 . Отсюда
. Отсюда  .
.

 Поскольку условие параллельности векторов
Поскольку условие параллельности векторов 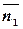 и
и  2 не выполняется, так как
2 не выполняется, так как 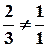 , стало быть,
, стало быть,  и
и 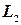 не параллельны.
не параллельны.
б) Перпендикулярными.
Прямые  и
и 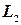 будут перпендикулярны, если
будут перпендикулярны, если 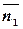

 2. Но условие перпендикулярности для векторов
2. Но условие перпендикулярности для векторов 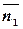 и
и  2 не выполняется, так как
2 не выполняется, так как 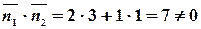 . Следовательно,
. Следовательно,  не перпендикулярна
не перпендикулярна 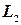 .
.
в) Найти угол  между
между  и
и 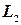 .
.
Угол между прямыми равен углу между их нормалями. Поэтому, используя формулу угла между двумя векторами, получим
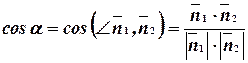 .
.
Так как  ,
,  ,
,  , то
, то 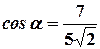 .
.