1. Имеются два варианта вложения капитала. Установлено, что при вложении капитала в мероприятие А получение прибыли в сумме 15 млн р. имеет вероятность 0,6, а в мероприятие В получение прибыли в сумме 20 млн р. – вероятность 0,4. Определите ожидаемое получение прибыли от вложения капитала (математическое ожидание) и рассмотрите вероятность наступления события объективным и субъективным методами.
РЕШЕНИЕ
Ожидаемое получение прибыли от вложения капитала (т.е. математическое ожидание) составит:
-по мероприятию А составит: МА = 15 х 0,6 = 9 млн. р.;
-по мероприятию В: МВ = 20 х 0,4 = 8 млн. р..
Вероятность наступления события может быть определена объективным методом или субъективным.
Так как МА ≥ Мв, наиболее предпочтителен вариант А.
Объективный метод определения вероятности основан на вычислении частоты, с которой происходит данное событие. Если известно, что при вложении капитала в какое-либо мероприятие прибыль в сумме 15 млн. р. была получена в 120 случаях из 200, то вероятность получения такой прибыли составляет 0,6 (120:200).
Субъективный метод определения вероятности основан на использовании субъективных критериев, которые основываются на различных предположениях. К таким предположениям могут относиться суждение оценивающего, его личный опыт, оценка эксперта, мнение финансового консультанта и пр. Когда вероятность определяется субъективно, то разные люди могут устанавливать разное ее значение для одного и того же события и таким образом делать различный выбор.
2. Оцените варианты финансовых вложений инвестора, с целью минимизации риска, используя методику вероятного распределения доходности.
Имеется два альтернативных варианта финансовых вложений с характеристиками, представленными в таблице.
Таблица. Характеристики финансовых инструментов
| Показатели | Варианты вложений | Вероятность осуществления, % | |
| А | Б | ||
| 1. Рыночная цена ценной бумаги, тыс. р. | |||
| 2. Экспертная оценка доходности: | |||
| 2.1. пессимистическая | |||
| 2.2. наиболее вероятная | |||
| 2.3. оптимистическая |
РЕШЕНИЕ
Среднее квадратическое отклонение (Ос):
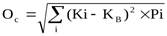
Коэффициент вариации:
Y=Ос:ОВДс,
где Ос - среднее квадратическое отклонение, ОВДс - средняя ожидаемая величина дохода
Определим среднюю ожидаемую величину дохода:
М = (9х0,25) + (11х0,6) + (14х0,15) = 10,95
Определим среднее квадратическое отклонение:
Ос = √(9-10,95) ² х 0,25 + (11-10,95) ² х 0,6 + (14-10,95) ² х 0,15 = 1,5
Определим коэффициент вариации:
К в = 1,5:10,95 = 0,14
Чем меньше коэффициент вариации, тем меньше риск.
3. Выберите наименее рискованный вариант вложения капитала путем сравнения значений коэффициентов вариации.
Первый вариант. Прибыль при средней величине 30 млн р. колеблется от 15 до 40 млн р. Вероятность получения прибыли в 15 млн р. равна 0,2 и прибыли в 40 млн р. – 0,3.
Второй вариант. Прибыль при средней величине 25 млн р. колеблется от 20 до 30 млн р. Вероятность получения прибыли в 20 млн р. равна 0,4 и прибыли в 30 млн р. – 0,3.
РЕШЕНИЕ
Первый вариант вложения капитала.
Определяем среднее квадратическое отклонение:
G² = 0,3 х (40-30)² + 0,2 х (30-15)² = 75
G = √75 = 8,66
Определяем коэффициент вариации:
Y = 8,66: 30 х 100 = 28,9 %
Второй вариант вложения капитала.
Определяем среднее квадратическое отклонение:
G² = 0,3 х (30-25) ² + 0,4 х (25-20) ² = 17,5
G = √17,5 = 4,18
Определяем коэффициент вариации:
Y = 4,18: 25 х100 = 16,7%
Сравнение значений коэффициентов вариации показывает, что меньшая степень риска присуща второму варианту вложения капитала.
4. Цена единицы продукции 2500 руб. Переменные издержки составляют 1500 руб. на единицу продукции. Объём реализации составляет 400 изделий в месяц.
1. Начальник отдела рекламы предлагает увеличить расходы на рекламу на 10000 руб., при этом выручка увеличится на 30 000 руб. Следует ли принимать решение об увеличении рекламного бюджета?
2. Заместитель генерального директора по производству предлагает использовать более дешевые материалы, что позволит экономить на переменных издержках по 250 руб. на каждой единице продукции. Однако, по мнению начальника отдела сбыта, это может привести к снижению качества и падению объема реализации до 350 штук в месяц. Следует ли применять более дешевые материалы?
3. Начальник отдела маркетинга предлагает снизить цену реализации на 200 руб. и одновременно довести расходы на рекламу до 150 000 руб. в месяц. В этом случае он прогнозирует увеличение объема продаж на 50%. Можно ли одобрить такое решение?
4. Начальник отдела сбыта предлагает изменить форму оплаты труда своих сотрудников: отменить оклады (суммарный месячный фонд оплаты составляет 60 000 руб.) и установить комиссионное вознаграждение 150 руб. с каждой проданной единицы продукции. Он уверен, что объем продаж вырастет на 15%. Следует ли согласиться с предложенным решением?
Представьте себя в роли ЛПР и дайте аргументированные ответы на поставленные вопросы.
5.Финансовый директор организации имеет возможность получить кредит банка на покупку оборудования под проценты на уровне 45% годовых. Одновременно он получает предложение получить оборудование по лизингу на следующих условиях:
• стоимость объекта лизинга — 36 000 руб.;
• период полной амортизации — один год, равномерно по месяцам;
• ежемесячные отчисления с учетом комиссионных лизингодателя (12%), кредитных, консультационных и других услуг составят 5% от остаточной стоимости оборудования.
Какой вариант решения должен выбрать финансовый директор?
6. Вдоль шоссе расположено 5 магазинов. Решается вопрос о строительстве базы снабжения. Магазины расположены на 2-м, 5-м, 25-м и 60-м км. Обработка статистических данных показала, что в среднем за период будут обращаться на базу: первый магазин – 5 раз, второй – 10 раз, третий -15 раз, четвертый -10 раз, пятый – 40 раз. Требуется решить вопрос о местонахождении базы снабжения так, чтобы сумма пробегов до базы была минимальной.
7. Какой проект для инвестирования из трех представленных выберет фирма, если для реализации каждого проекта требуются одинаковые объемы инвестиций, а планируемый доход известен в виде распределения вероятностей?
| Проект 1 | Проект 2 | Проект 3 | |||
| Доход (у.е.) | вероятность | Доход (у.е.) | вероятность | Доход (у.е.) | вероятность |
| 0,2 | 0,3 | 0,3 | |||
| 0,6 | 0,5 | 0,5 | |||
| - | 0,2 | 0,2 |
8. Финансовый директор организации имеет возможность получить кредит банка на покупку оборудования под проценты на уровне 20% годовых. Одновременно он получает предложение получить оборудование по лизингу на следующих условиях:
• стоимость объекта лизинга — 48 000 руб.;
• период полной амортизации — один год, равномерно по месяцам;
• ежемесячные отчисления с учетом комиссионных лизингодателя (12%), кредитных, консультационных и других услуг составят 5% от остаточной стоимости оборудования.
Какой вариант решения должен выбрать финансовый директор?
9. Финансовый директор организации имеет возможность получить кредит банка на покупку оборудования под проценты на уровне 40% годовых. Одновременно он получает предложение получить оборудование по лизингу на следующих условиях:
• стоимость объекта лизинга — 72 000 руб.;
• период полной амортизации — один год, равномерно по месяцам;
• ежемесячные отчисления с учетом комиссионных лизингодателя (12%), кредитных, консультационных и других услуг составят 5% от остаточной стоимости оборудования.
Какой вариант решения должен выбрать финансовый директор?
10. Какой проект для инвестирования из трех представленных выберет фирма, если для реализации каждого проекта требуются одинаковые объемы инвестиций, а планируемый доход известен в виде распределения вероятностей?
| Проект 1 | Проект 2 | Проект 3 | |||
| Доход (у.е.) | вероятность | Доход (у.е.) | вероятность | Доход (у.е.) | вероятность |
| 0,2 | 0,25 | ? | |||
| 0,38 | ? | 0,45 | |||
| ? | 0,35 | 0,2 |
11. Фирма рассматривает инновационный проект со следующими характеристиками. Затраты на проект единовременные и составляют J0 = 150 тыс. у.е., цена капитала р = 12%, ожидается получить от инновации доходы (по годам) в размерах: Р1 = 30 тыс. у.е., Р2= 70 тыс. у.е., Р3 = 70 тыс. у.е., Р4 = = 45 тыс. у.е. Примет ли фирма в этих условиях проект к реализации?
Рассчитать индекс рентабельности.
12. Проанализировать проект со следующими характеристиками (тыс. у.е.): J0= 150, Р1 = 30, Р2 = 70, Р3 = 70, Р4 = 45. Ожидается, что цена капитала будет меняться по годам следующим образом: 12%, 13%, 14%, 14%.
13. Рассчитать индекс рентабельности для инновационного проекта со следующими данными (тыс. у.е.): J0 = 200, Р, = 40, Р2 = 70, Р3= 90, Р4 = 150,
цена капитала 20%.
14. Фирма решает вопрос о выборе проекта для инвестирования. На рассмотрение представлено два проекта с одинаковой суммой инвестиций. Величина прогнозного дохода известна в виде распределения вероятностей. Данные сведены в таблицу.
| Проект 1 | Проект 2 | ||
| доход (у.е.) | вероятность | доход (у.е.) | вероятность |
| 0,5 | 0,7 | ||
| 0,3 | 0,2 | ||
| 0,2 | 0,1 |
Какой проект для реализации выберет фирма?
15. Какой проект для инвестирования из трех представленных выберет фирма, если для реализации каждого проекта требуются одинаковые объемы инвестиций, а планируемый доход известен в виде распределения вероятностей?
| Проект 1 | Проект 2 | Проект 3 | |||
| Доход (у.е.) | вероятность | Доход (у.е.) | вероятность | Доход (у.е.) | вероятность |
| 0,4 | 0,3 | 0,3 | |||
| 0,6 | 0,5 | 0,5 | |||
| - | - | 0,2 | 0,2 |