Лабораторная работа №_
Исследование мезоструктуры и фрактальных свойств
Наноструктурируемых систем на установке малоуглового рассеяния
Поляризованных нейтронов «Вектор» реактора ВВР-М
Рунов В.В., Григорьев С.В., Окороков А.И., Копица Г.П.
Цель работы
Ознакомление с методикой проведения эксперимента и обработкой данных по малоугловому рассеянию нейтронов на фрактальных объектах.
ФРАКТАЛ – объект, состоящий из частей, которые в каком-то смысле подобны целому (Мандельброт) [1]
Введение
Явления фрактальной агрегации широко распространены в наноструктурирумых системах. Типичными примерами фрактальных сред являются нанопорошки, силикаты, силикагели, аэрогели, полимерные растворы, гели и композиты, коллоиды (рис. 1), микропористые среды, неорганические и органические золь-зель нанокомпозиты. В конце прошлого столетия было установлено[2], что формирование структуры подобных материалов происходит путем развития самоподобных структур, или фрактальных агрегатов, которые могут быть количественно описаны в рамках концепции фрактальной размерности - величины, которая характеризует степень заполнения объектом пространства.
Рис. 1. Фрактал, образующийся при агрегации коллоидных частиц золота
При этом, поскольку реальный фрактальный объект, в отличие от математического, всегда имеет ограничение по размерам, второй важной характеристикой фракталов является диапазон самоподобия, в котором объект является фрактальным. Диапазон самоподобия ограничен двумя пределами: нижним - размером начальной частицы или поры, - и верхним - размером агрегата или кластера.
Таким образом, концепция фрактальности нашла, в настоящее время, применение для описания самых разнообразных материалов, ранее характеризовавшихся как бесструктурные.
Среди методов, используемых для исследования фрактальной размерности, наиболее информативными и точными являются неразрушающие методы измерения в обратном пространстве (в импульсном пространстве), основанные на анализе Фурье-образов фрактальных объектов, полученных при рассеянии ими света, рентгеновских лучей и нейтронов.
Общие принципы малоуглового рассеяния
Механизмы описания базовых принципов малоуглового рассеяния являются общими, как для нейтронов, так и электромагнитного излучения (рентгеновских лучей, света). В общем виде схема малоуглового эксперимента представлена на Рис. 2.
Рис. 2. Схема эксперимента по малоугловому рассеянию.
В основе метода лежит описание взаимодействия плоской монохроматической волны 
(где 
− волновой вектор рассеиваемой частицы в начальном состоянии) с точечным силовым центром (например, ядром). Благодаря взаимодействию центр становится источником излучения, которое на больших расстояниях 
имеет вид расходящейся сферической волны. В результате асимптотический вид волновой функции при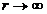 
записывается следующим образом:
(1)
где 
- волновой вектор частицы, рассеянной в том направлении, в котором производится наблюдение. В рассматриваемом нами случае упругого рассеяния, то есть рассеяния без передачи энергии, 
, а угол рассеяния определяется условием:
. (2)
Функция 
называется амплитудой рассеяния и имеет размерность длины.
Отметим, что:
1. Если длина волны рассеиваемой частицы велика по сравнению с размерами рассеивателя (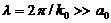
), то амплитуда рассеяния не зависит от угла рассеяния 
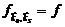(s- рассеяние). В случае медленных нейтронов l ~ 10-8 см, а размер ядра а 0 ~ 10-12 ¸ 10-13 см, поэтому рассеяние отдельным ядром всегда можно считать s- рассеянием.
2. В низшем, так называемом борновском приближении, амплитуда рассеяния зависит только от переданного импульса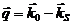 
.
Итак, взаимодействие с отдельным ядром характеризуется не зависящей от угла рассеяния амплитудой рассеяния f. Однако в нейтронной физике принято вместо f пользоваться длиной рассеяния b = − f, которую часто называют амплитудой рассеяния. Если мы имеем систему ядер (атомов), то каждое из них является источником рассеянной волны и необходимо учитывать интерференцию этих волн. Для одного центра, находящегося в точке с координатами 
, фаза амплитуды рассеяния определяется фактором 
, где первый множитель – это та фаза, с которой волна подошла к рассеивателю, а второй – фаза, с которой она вышла.В результате амплитуду рассеяния от группы из N ядер (атомов) c координатами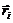 
надо записать в виде:
. (3)
В случае сплошной среды, амплитуда упруго и когерентно рассеянной волны имеет вид:
(4)
где r (r) – пространственное распределение плотности когерентной амплитуды рассеяния, интегрирование распространяется на весь объем исследуемого образца V.
В эксперименте измеряется не амплитуда, а интенсивность рассеяния, которая пропорциональна потоку энергии (квантов излучения), прошедшей через единицу площади. Энергия, в свою очередь, пропорциональна квадрату скорости, то есть она пропорциональна квадрату модуля амплитуды рассеяния, которая, вообще говоря, есть комплексная величина:
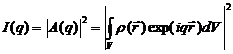. (5)
Полученная формула связывает интенсивность рассеяния с распределением плотности в реальном пространстве посредством Фурье преобразования. Отметим, что интенсивность рассеяния с переданным импульсом q, который связан с длинной волны используемого излучения l и углом рассеяния q соотношением q = 4p×sinq/l, соответствует анализу распределения плотности в реальном пространстве с разрешением 2p/ q. В совокупности эти методы позволяют получить информацию о надмолекулярной структуре материалов в интервале характерных размеров от 0.1 до 1000 нм. Вид выбора излучения зависит как от размеров фрактальных объектов, так и от природы исследуемого материала.