ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №10
ТЕМА: Интегрирование линейного дифференциального уравнения
Интегрирование линейного однородного дифференциального уравнения
Имеем уравнение  .
.
В этом уравнении легко разделяются переменные
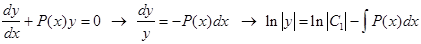
Отсюда, потенцируя, находим общее решение уравнения
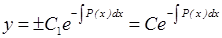 .
.
Пример 57. Найти решение уравнения  .
.
 ;
;
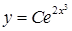 - в чем легко убедиться, подставив данное решение в исходное дифференциальное уравнение.
- в чем легко убедиться, подставив данное решение в исходное дифференциальное уравнение.
Интегрирование линейного неоднородного дифференциального уравнения (ЛНДУ).
Для решения ЛНДУ
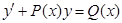
наиболее распространенными методами решения ЛНДУ первого порядка (ЛНДУ 1) являются методы, разработанные Лагранжем и Бернулли.
Метод Лагранжа (метод вариации произвольной постоянной)
Теория:
1) находим решение соответствующего ЛОДУ1  , как показано выше в виде
, как показано выше в виде 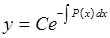 ;
;
2) заменяем произвольную постоянную 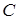 в предыдущем решении некоторой (пока неизвестной) функцией
в предыдущем решении некоторой (пока неизвестной) функцией  :
:  ;
;
3) так как последнее выражение должно быть решением исходного ЛНДУ1, оно должно удовлетворять этому уравнению; следовательно необходимо выполнить действия аналогичные проверке правильности найденного решения:
- находим производную

- подставляем выражения для 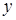 и
и 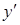 в исходное уравнение, после очевидных преобразований получаем
в исходное уравнение, после очевидных преобразований получаем
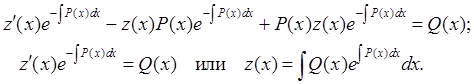
4) находим общее решение линейного уравнения
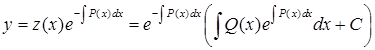
Несмотря на громоздкость вышеприведенных выражений, использование данного метода для решения конкретных дифференциальных уравнений достаточно компактно.
Пример 58.
Найти общее решение уравнения  .
.
Решение.
1. Рассмотрим сначала соответствующее однородное уравнение
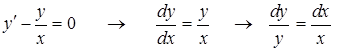
Получено уравнение с разделяющимися переменными

2. В полученном решении однородного уравнения выполним замену 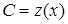 , найдем производную и подставим в исходное неоднородное уравнение
, найдем производную и подставим в исходное неоднородное уравнение

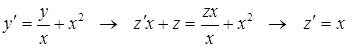
Вновь получено уравнение с разделяющимися переменными (для функции 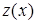 )
)
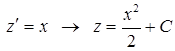
3. Подставим полученное решение для функции 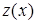 в решение однородного уравнения (вместо произвольной постоянной), получим общее решение исходного уравнения
в решение однородного уравнения (вместо произвольной постоянной), получим общее решение исходного уравнения

это и есть ОР ЛНДУ1(общее решение линейного неоднородного ДУ1)
Вывод: для интегрирования ЛНДУ1 методом Лагранжа необходимо найти решения двух уравнений с разделяющимися переменными
Метод Бернулли (метод подстановки)
Теория:
1) искомая функция представляется в виде произведения двух заранее неизвестных функций 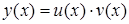 или в сокращенной записи
или в сокращенной записи 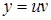 ;
;
2) находим производную искомой функции и (вместе с функцией) подставляем в уравнение (получаем преобразованное уравнение)
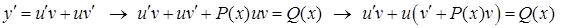
3) так как одна из функций 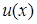 или
или  может иметь произвольный вид, выберем функцию
может иметь произвольный вид, выберем функцию  так, чтобы выражение в круглых скобках было равно нулю
так, чтобы выражение в круглых скобках было равно нулю
 ;
;
4) получено уравнение с разделяющимися переменными, откуда может быть легко найдена функция  :
:

(произвольная постоянная при интегрировании принята равной нулю)
5) найденная функция  подставляется в преобразованное уравнение (выражение в скобке равно нулю!)
подставляется в преобразованное уравнение (выражение в скобке равно нулю!)
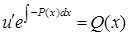
6) получено уравнение с разделяющимися переменными, откуда может быть легко найдена функция 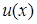 :
:

7) так как 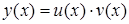 , то
, то
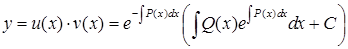 .
.
При использовании этого метода, также необходимо найти решения двух уравнений с разделяющимися переменными, причем эти уравнения идентичны для обоих методов. Здесь, как и в предыдущем методе, решение в общем виде представляет собой достаточно громоздкие выражения, однако, использование данного метода для решения конкретных дифференциальных уравнений достаточно компактно.
Практика
Пример 59. Найти общее решение уравнения 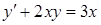 .
.
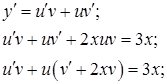
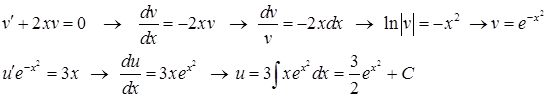
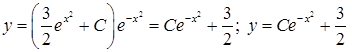 .
.
Выполним проверку правильности решения: найдем производную найденной функции и подставим её в исходное уравнение
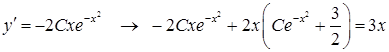 - уравнение обратилось в тождество, значит, решение верное.
- уравнение обратилось в тождество, значит, решение верное.
Пример 60.
Найти частное решение уравнения 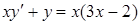 ;
; 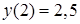 .
.
Преобразуем уравнение
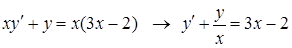 .
.
Найдем общее решение методом Бернулли
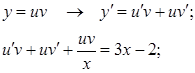

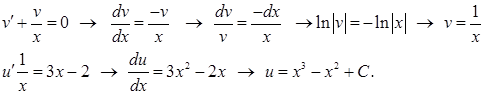
Получаем общее решение уравнения 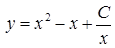 .
.
Подставим начальное условие и найдем значение произвольной постоянной
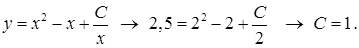
Получаем частное решение уравнения 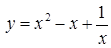 .
.
Замечание. Если задача состоит в нахождении частного решения дифференциального уравнения, то проверка правильности найденного решения состоит из 2-х обязательных этапов:
1) проверка соответствия найденного решения заданному уравнению;
2) проверка соответствия найденного решения начальному условию.