ТЕОРЕТИЧЕСКИЕ ЗАДАЧИ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
1. Доказать, что если все элементы определителя 3-го порядка равны ±1, то сам определитель будет четным числом.
2. Найти наибольшее значение, которое может принимать определитель 3-го порядка, при условии, что все его элементы равны ±1.
3. Найти наибольшее значение определителя 3-го порядка, все элементы которого равны 1 или 0.
4. Как изменится определитель порядка п, если у всех его элементов изменить знак на противоположный?
5. Сколько миноров порядка к содержит квадратная матрица порядка п?
6. Найти значения λ, при которых матрица
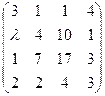
имеет наименьший ранг. Чему равен ранг при найденных λ и чему он равен при других значениях λ?
7. Чему равен ранг матрицы 
при различных значениях λ?
8. Доказать, что если матрица содержит т строк и имеет ранг r, то любые s ее строк образуют матрицу, ранг которой не меньше r + s – m.
9. Как изменится ранг матрицы, если к ней добавить одну строку или один столбец?
10. Доказать, что ранг суммы двух матриц не больше суммы их рангов.
11. Доказать, что если ранг матрицы А не меняется при добавлении к ней любого столбца матрицы В (с таким же числом строк, как А), то он не изменится при добавлении к матрице А всех столбцов матрицы В.
12. Выяснить, являются ли следующие системы векторов линейно независимыми:
а) а = {1; 2; 3}, b = {3; 6; 7}; б) a = {2; -3; 1}, b = {3; -1; 5}, c = {1; -4; 3}.
13. Выяснить, являются ли следующие системы векторов линейно независимыми:
а) а = {4; -2; 6}, b = {6; -3; 9}; б) a = {5; 4; 3}, b = {3; 3; 2}, c = {8; 1; 3}.
14. Доказать, что система векторов, содержащая два равных вектора, линейно зависима.
15. Доказать, что система векторов, содержащая нулевой вектор, линейно зависима.
16. Доказать, что если часть системы векторов линейно зависима, то и вся система линейно зависима.
17. Доказать, что любая часть системы линейно независимых векторов линейно независима.
18. Исследовать систему и найти общее решение в зависимости от значения параметра λ:
.
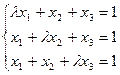19. Исследовать систему и найти общее решение в зависимости от значения параметра λ:
.
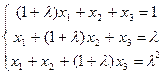20. Исследовать систему и найти общее решение в зависимости от значения параметра λ:
.
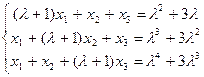21. Привести пример несовместной системы 3-х линейных уравнений с тремя неизвестными, у которой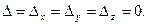 
22. Найти условия, необходимые и достаточные для того, чтобы либо сумма двух решений, либо произведение одного решения на ненулевое число было снова решением той же системы линейных уравнений.
23. При каких условиях в любом решении совместной системы линейных уравнений неизвестное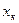 
имеет одно и то же значение?
24. Найти условия, необходимые и достаточные для того, чтобы в любом решении совместной системы линейных уравнений к -е неизвестное было равно нулю.
25. Доказать, что если для матриц А и В оба произведения АВ и ВА существуют, причем АВ = ВА, то матрицы А и В квадратные и имеют одинаковый порядок.
26. Как изменится произведение АВ матриц А и В, если переставить i – ю и j -ю строки матрицы А?
27. Как изменится произведение АВ матриц А и В, если переставить i – й и j -й столбцы матрицы В?
28. Доказать, что если А и В – квадратные матрицы одного порядка, причем АВ ≠ ВА, то:
а) (А + В)2 ≠ А2 +2АВ + В2;
б) (А + В)(А – В) ≠ А2 – В2.
29. Найти все матрицы второго порядка, квадрат которых равен нулевой матрице.
30. Найти все матрицы второго порядка, квадрат которых равен единичной матрице.
31. Как изменится обратная матрица А-1, если в данной матрице А:
а) переставить i – ю и j -ю строки;
б) i – ю строку умножить на число с, не равное нулю;
в) к i – й строке прибавить j -ю, умноженную на число с, или совершить аналогичное преобразование столбцов?
32. Пусть АТ – матрица, транспонированная по отношению к матрице А. Доказать, что
а) (х А)Т = х АТ; б) (А + В)Т = АТ + ВТ; в) (АТ)Т = А.
33. Доказать равенство (АВ)Т = ВТАТ.
34. При каких значениях с совместна система уравнений: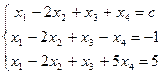 
?
35. При каких значениях с совместна система уравнений: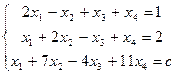 
?
36. Известно, что столбцы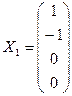 
и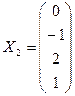 
образуют фундаментальную систему решений некоторой однородной системы линейных уравнений. Из скольких уравнений может состоять эта система? Привести пример такой системы, состоящей из трех уравнений.
37. Найдите две различные фундаментальные системы решений для системы уравнений
х 1 + х 2 + х 3 + х 4 = 0.
38. Найдите две различные фундаментальные системы решений для системы уравнений
.
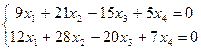39. Найти однородную систему линейных уравнений, состоящую из двух уравнений, для которой столбцы
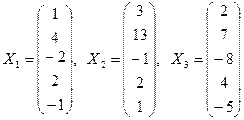
образуют ее фундаментальную систему решений.
40. Найти однородную систему линейных уравнений, состоящую из трех уравнений, для которой столбцы
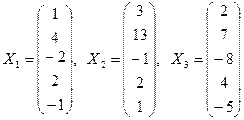
образуют ее фундаментальную систему решений.
41. Найти однородную систему линейных уравнений, состоящую из четырех уравнений, для которой столбцы
образуют ее фундаментальную систему решений.
42. Существует ли однородная система линейных уравнений, для которой каждая из совокупностей трех столбцов:
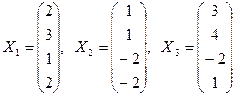и 
является ее фундаментальной системой решений?
43. Докажите, что существует неоднородная система линейных уравнений, для которой каждая из формул
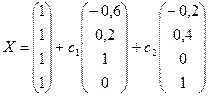и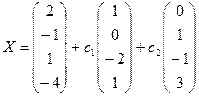 
описывают ее общее решение. Приведите пример такой системы уравнений.