Решение задач линейного программирования произведем на основе алгоритма обратной матрицы Канторовича, именуемого еще модифицированным симплекс-алгоритмом, применимо к следующей модели:
AX=B; (2.1)
X ≥0,
где А – прямоугольная (m ∙ n) – матрица условий
,
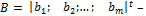вектор ограничений;
– вектор-строка коэффициентов линейной формы;
– вектор управляющих переменных.
Будем считать задачу линейного программирования представленной в канонической форме по Канторовичу, если она записана в виде (2.1).
Метод обратной матрицы позволяет, начиная расчет с некоторого начального опорного плана и постепенно улучшая его, получить через определенное число итераций оптимальный план или убедиться в неразрешимости задачи.
Для дальнейшего изложения сущности и вычислительной процедуры алгоритма обратной матрицы введем следующие дополнительные обозначения:
Ах – квадратная матрица условий порядка m, отвечающая базисным компонентам опорного плана;
– матрица условий размером m ∙ (n – m), отвечающая внебазисным переменным опорного плана;
Сх – вектор-строка коэффициентов линейной формы, отвечающая базисным компонентам опорного плана;
– вектор-строка коэффициентов линейной формы, отвечающая внебазисным компонентам опорного плана;
ᴧ – вектор-строка множителей Лагранжа;
Δ – вектор-строка оценок внебазисных вектор-условий относительно базиса опорного плана;
Хik – составляющие разложения вектора Аk, подлежащего вводу в базис, по текущему базису;
Аsr – вектор, подлежащий удалению из текущего базиса.
Матрицы А, В, С, 
Сх, считаются известными, если задача линейного программирования представлена в канонической форме по Канторовичу, найден начальный опорный план Х 0 и выбран базис. Поскольку задача считается поставленной корректно и, стало быть, ограничения ее линейно независимы, то определитель матрицы Ах отличен от нуля и существует обратная матрица Ах -1. Существавание этой обратной матрицы определяет всю вычислительную схему рассматриваемого алгоритма.
Каждая итерация вычислительного процесса состоит из двух этапов. На первом осуществляется проверка оптимальности исследуемого опорного плана, и если он таковым не является, то переходят ко второму этапу. Он состоит в проведении элементарного преобразования, заключающегося в выборе вектора Ак, который вводится в новый базис, и вектора Аsr, который исключается из старого базиса. После этого вычисляются базисные компоненты нового опорного плана и все параметры, необходимые для продолжения вычислительного процесса.
Сформируем теперь алгоритм обратной матрицы.
1. Найти очередной (начальный) опорный план, сформировать его базис и матрицы Ах, Сх, 
2. Вычислить обратную матрицу 
.
3. Вычислить вектор-строку множителей Лагранжа:
. (2.2)
4. Вычислить вектор-строку оценок:
(2.3)
5. Если все Δ j > 0, то план оптимален, иначе следует перейти к шагу 6.
6. Определить вектор Ак для введения в базис.
7. Вычислить компоненты:
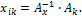(2.4)
8. Если все 
< 0, то задача неразрешима, иначе следует перейти к шагу 9.
9. Определить вектор Аsr для удаления из базиса и возвратиться к шагу 1.
К изложенному алгоритму сделаем несколько пояснений.
Вектор Ак, подлежащий введению в базис, определяется из рассмотрения оценок Δ j. Вектор Ак – это вектор условий с отрицательной оценкой (обычно с минимальной из всех отрицательных оценок):
(2.5)
По этому признаку выявляется позиция, которую занимает соответствующая Ак внебазисная переменная среди нулевых значений текущего опорного плана. Например, позиция определяется местом расположения минимальной отрицательной оценки в вектор-строке Δ.
Вектор Аsr, подлежащий удалению из базиса, определяется с использованием составляющих разложения 
. Вектор Аsr – это вектор, на котором достигается
, 
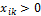, (2.6)
где 
– базисные компоненты текущего опорного плана. По этому признаку выявляется позиция, которую занимает соответствующая Аsr базисная переменная среди ненулевых значений текущего опорного плана. Номер позиции определяется местом расположения положительного члена вектора , отвечающего минимуму отношения 
.
Базисные компоненты очередного опорного плана для его формирования на первом шаге алгоритма вычисляются так:
. (2.7)
Ясно, что полученный по (2.7) вектор имеет размерность, равную числу ограничений модели.
При решении реальных задач линейного программирования во многих случаях начальный опорный план очевиден. Однако иногда возникают трудности в его назначении. В этих случаях вводится вспомогательный алгоритм.
Алгоритм поиска начального опорного плана
1. Записать задачу линейного программирования в канонической форме по Канторовичу.
2. Произвольно назначить 
– набор вектор-условий, отвечающих потенциальному начальному опорному плану.
3. Сформировать матрицу Ах.
4. Вычислить обратную матрицу .
5. Вычислить по (2.7) вектор базисных компонент предполагаемого начального опорного плана.
6. если все компоненты вектора 
, то начальный опорный план найден, в противном случае изменить и возвратиться к шагу 3.
2.1. Статическая оптимизация электрической сети
Рассмотрим сетевую статическую задачу, состоящую в нахождении наилучшей в смысле линеаризованных приведенных затрат конфигурацию сети. Такая задача при ограничениях по первому закону Кирхгофа сводится к линейной схеме.
Пример.2.1. Найти оптимальный статический граф двухцепной сети 110 кВ (рис. 2.1) при наличии следующих исходных данных:
Рис. 2.1. Максимальный граф сети
Нагрузки узлов (МВт):
Длины дуг графа (км):
.
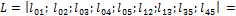
Линеаризованные приведенные затраты (тыс.руб./км) в линиях электропередач 01, 02, 03, 04, 05:
если 
;
в остальных линиях:
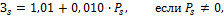
если ;
Будем исходить из следующей математической модели:
.
Ее развернутая функциональная форма:
З= (1,15+0,008∙ P 01) ∙ 35,0 + (1,15+0,008∙ P 02) ∙ 35,0 + (1,15+0,008∙ P 03) ∙
∙ 29,4 +(1,15+0,008∙ P 04) ∙ 26,0 +(1,15+0,008∙ P 05) ∙ 30,0 + (1,01+0,01∙ P 12) ∙
∙ 37,4 + (1,01+0,01∙ P 13) ∙ 20,4 + (1,01+0,01∙ P 35) ∙ 42,0 + (1,01+0,01∙ P 45) ∙
∙ 35,0→ min;
(2.9)
;
Введем следующие обозначения:
P 01 = x 1;
P 02 = x 2;
P 03 = x 3;
P 04 = x 4;
P 05 = x 5;
P 12 = x 6 – x 7; (2.10)
P 12 = x 6 – x 7;
P 13 = x 8 – x 9;
P 35 = x 10 – x 11;
P 45 = x 12 – x 13.
С учетом этого модель (2.9):
З = К + 0,28∙ x 1 + 0,28∙ x 2 + 0,2352∙ x 3 + 0,208∙ x 4 + 0,24∙ x 5 + 0,374∙ x 6 – 0,374∙ x 7 + 0,204∙ x 8 – 0,204∙ x 9 + 0,42∙ x 10– 0,42∙ x 11 + 0,35∙ x 12 – 0,35∙ x 13 → min;
x 1 – x 6 + x 7 – x 8 + x 9 = 1,0;
x 2 + x 6 – x 7 = 32,0; (2.11)
x 3 + x 8 – x 9 – x 10 + x 11 =25;
x 4 – x 12 + x 13 = 27,0;
x 5 + x 10 – x 11 + x 12 – x 13 = 35,0;
xj > 0, j = 1, 2, …, 13,
где К – свободный член, то есть некоторая постоянная.
Представим модель (2.11) в канонической форме по Канторовичу. Поскольку свободный член не изменяет вектора управления, его можно временно исключить. Тогда модель примет форму:
X ≥ 0; (2.12)
.
Разрешим задачу отыскания наилучшего статического графа сети методом обратной матрицы. Примем предположительно на первой итерации:
.
Сформируем матрицы Ах, 
Сх, :
;
;
.
Обратная матрица от Ах:
.
Определим базисные компоненты начального опорного плана:
Таким образом, предположения о базисных компонентах верны и начальный опорный план примет вид:
= 
140; 0; 0; 0; 32; 0;53; 62; 0; 0; 
t.
Проверим его оптимальность:
.
∙ 
.
Вектор управления 
не является оптимальным, так как среди оценок имеются отрицательные.
Введем в базис вектор А 5, поскольку 
.Это число занимает четвертую позицию в векторе оценок, а четвертая позиция среди внебазисных переменных соответствует А 5. С целью определения вектора условий, подлежащего удалению из базиса, вычислим компоненты:
и найдем
Отсюда следует, что выводить из базиса необходимо вектор условий А 10.
Таким образом, на второй итерации:
.
Сформируем матрицы Ах, Сх, :
; 
;
.
Обратная матрица от Ах:
.
Определим базисные компоненты нового опорного плана:
Очередной опорный план:
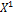= 78; 0; 68; 32; 0; 0; 0; 53; 0; 0; 
t.
Проверим его оптимальность:
.
∙ 
.
Вектор управления 
не является оптимальным, так как среди оценок имеются отрицательные.
Будем вводить в базис вектор А 11, поскольку min(–0,1252;–0,4152) = – 4152.
Вычислим:
и найдем
Таким образом, на третьей итерации
.
Сформируем матрицы Ах, Сх, :
; 
;
.
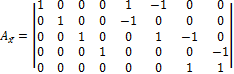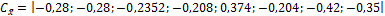Обратная матрица от Ах:
.
Определим базисные компоненты нового опорного плана:
Очередной опорный план:
= 
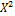140; 32; 0; 0; 53; 0; 78;0; t.
Проверим его оптимальность:
.
∙ 
.
План 
оптимален, так как среди оценок нет отрицательных.
Таким образом
= 140; 32; 0; 0; 53; 0; 78; 0; t.
С целью проверки и интерпретации полученных результатов обратимся к (2.10):
P 01 = x 1 = 0;
P 02 = x 2 = 0;
P 03 = x 3 = 0;
P 04 = x 4 = 0;
P 05 = x 5 = 140 МВт;
P 12 = x 6 – x 7 = 32 МВт
P 13 = x 8 – x 9 = -53 МВт;
P 35 = x 10 – x 11 = -78 МВт;
P 45 = x 12 – x 13 = -27 МВт.
Отрицательные результаты означают, что в оптимальном графе сети нужно сменить на противоположные в сравнении с исходным максимальным графом направления потоков мощности в дугах 13, 35, 45, а дуги 01, 02, 03, 04 вообще исключить из рассмотрения, поскольку там протекают «нулевые» потоки.
Окончательно оптимальный граф
.
Рассмотрим как изменились по итерациям приведенные затраты, представляющие собой критерий исследуемой операции. Для этого векторы управления 
подставим в целевую функцию модели (2.11) или соответствующие им мощности – в (2.9). Отсюда:
З(Х 0) = 365,532 тыс.руб.;
З(Х 1) = 341,2296 тыс.руб.;
З(Х 2) = 307,404 тыс.руб.
После каждой итерации критериальная функция улучшалась. Учитывая строгое соответствие каждого опорного плана системе ограничений, можно говорить о действительной оптимизации конфигурации сети.