Факультет фундаментальной медицины

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Имени М. В. Ломоносова

Факультет фундаментальной медицины

 

 

Шевченко Остап Александрович, 103 гр.

 

 

Понятие о совместной функции распределения случайных величин. Доверительные интервалы для параметра а в случае выборки из нормального распределения N (а,σ²): а) при известном σ²; б) при неизвестном σ². Творческое задание (U -тест Манна — Уитни (на примере научной статьи))

Реферат по курсу основ теории вероятностей

и математической статистики

 

 

Москва

Оглавление:

Билет №6. Вопрос 1. Понятие о совместной функции распределения случайных величин.…………………………………………………………………………….. 3-5

Билет №6. Вопрос 2. Доверительные интервалы для параметра а в случае выборки из нормального распределения N (а,σ²): а) при известном σ²; б) при неизвестном σ²…………………………………………………………………………………….. 6-8

Творческое задание. Анализ статьи «Inflammation, Aspirin, and the Risk of Cardiovascular Disease in Apparently Healthy Men»…………………………………………………………………………..….... 9-11

Билет №6. Вопрос 1. Понятие о совместной функции распределения случайных величин. [1, 2]

Функция называется функцией распределения вектора или функцией совместного распределения случайных величин .

Перечислим свойства функции совместного распределения. Для простоты обозначений ограничимся вектором ( из двух величин.

Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств X < x и Y < y:

F (x,y) = P((X<x)(Y<y)) (1)

Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения F (x,y) есть не что иное, как вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной в точке (х, у), лежащий левее и ниже ее (рис. 1). В аналогичной интерпретации функция распределения одной случайной величины Х - обозначим ее F₁(x) - представляет собой вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой х (рис. 2); функция распределения одной величины Y – F₂(у) - вероятность попадания в полуплоскость, ограниченную ординатой у (рис. 3).

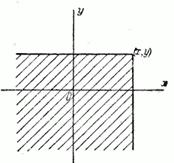
Рис. 1

Сформулируем основные свойства для функции распределения системы случайных величин и воспользуемся геометрической интерпретацией для наглядной иллюстрации этих свойств.

Свойство 1. Функция распределения F (x,y) есть неубывающая функция обоих своих аргументов, т. е.:

при х₂ > x₁ F(х₂,y) ≥ F(x₁,y);

при y₂ > y₁ F(х,y₂) ≥ F(x,y₁).

В этом свойстве функции F(x) можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадании в квадрант с вершиной (x,y) (рис. 1). Действительно, увеличивая x (смещая правую границу квадранта вправо) или увеличивая y (смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероятность попадания в этот квадрант.

Рис.2 Рис. 3

Свойство 2. Повсюду на -ꝏ функция распределения равна нулю:

F(х, -ꝏ) = F(-ꝏ,y) = F (-ꝏ, -ꝏ) = 0.

В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта (x→ -ꝏ) или вниз его верхнюю границу (y→ -ꝏ) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.

Свойство 3. При одном из аргументов, равном +ꝏ, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:

F(х, +ꝏ) = F₁(x);

F (+ꝏ, y) = F₂(y),

где F₁(x), F₂(y) - соответственно функции распределения случайных величин X и Y.

В этом свойстве функции распределения можно наглядно убедиться, смещая ту или иную из границ квадранта на +ꝏ; при этом в пределе квадрант превращается в полуплоскость, вероятность попадания в которую есть функция распределения одной из величин, входящих в систему.

Свойство 4. Если оба аргумента равны +ꝏ, функция распределения системы равна единице:

F (+ꝏ, +ꝏ) = 1.

Действительно, при x→ +ꝏ, y→ +ꝏ квадрант с вершиной (x,y) в пределе обращается во всю плоскость xOy, попадание в которую есть достоверное событие.

Для системы двух случайных величин актуальным является вопрос о вероятности попадания случайной точки (Х, Y) в пределы заданной области D на плоскости xOy (рис. 4).

Рис. 4

Условимся событие, состоящие в попадании случайной точки (Х, Y) в область D, обозначать символом (Х, Y) ⸦ D.

Вероятность попадания случайной точки в заданную область выражаются наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.

Выразим через функцию распределения системы вероятность попадания случайной точки (Х, Y) в прямоугольник R, ограниченный абсциссами α и β и ординатами γ и δ (рис. 5).

При этом следует условиться, куда мы будем относить границы прямоугольника. Аналогично тому, как мы делали для одной случайной величины, условимся включать в прямоугольник R его нижнюю и левую границы и не включать верхнюю и правую. Тогда событие (Х, Y) ⸦ R будет равносильно произведению двух событий: α ≤ X ≤ β и γ ≤ Y ≤ δ. Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости xOy четыре бесконечных квадранта с вершинами в точках (β, δ); (α, δ); (β, γ); и (α, γ) (рис. 6).

Рис. 5 Рис. 6

Очевидно, вероятность попадания в прямоугольник равна вероятности попадания в квадрант (β, δ) минус вероятность попадания в квадрант (α, δ) минус вероятность попадания в квадрант (β, γ) плюс вероятность попадания в квадрант (α, γ) (так как мы дважды вычли вероятность попадании в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:

P((X, Y) ⸦ R) = F(β, δ) - F(α, δ) - F(β, γ) + F(α, γ).

 

Билет №6. Вопрос 2. Доверительные интервалы для параметра а в случае выборки из нормального распределения N (а,σ²): а) при известном σ²; б) при неизвестном σ² [3]

Пусть имеется выборка X₁...X_n из некоторого закона распределения, и мы хотим оценить параметр этого закона θ – это может быть, например, математическое ожидание или дисперсия. Доверительным интервалом для параметра θ с уровнем доверия β мы будем считать такой интервал (A; B), что P(A<θ<B) = β. Задача интервального оценивания – найти такие границы A и B.

То, что следует запомнить: доверительный интервал тем шире, чем выше уровень доверия.

Доверительный интервал для математического ожидания (μ) в случае нормальной генеральной совокупности и известной дисперсии.

Так как генеральная совокупность нормальна, то в данном случае, независимо от размера выборки, выборочное среднее имеет нормальное распределение: 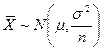. Таким образом, случайная величина имеет стандартное нормальное распределение. Пусть нам нужно построить доверительный интервал с уровнем доверия 1-α (часто говорят «100(1-α)% доверительный интервал»), то есть α – вероятность (риск) того, что оцениваемый параметр окажется вне этого интервала. Найдём такое число z, что 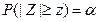. Искать это число нужно из таблицы стандартного нормального распределения с учётом того, что 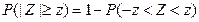, а для различных значений z таблицы хранят соответствующие значения P(-z<Z<z). Таким образом, зная α, мы подбираем подходящее значение z. Например, если нужно построить 95% доверительный интервал, то есть 1-α=0,95, то нужное нам значение z будет равно 1,96. Для уровня доверия 99% надо взять z=2,58. Теперь вернёмся к выборочному среднему:

.

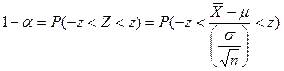Вынесем все переменные, кроме μ, из средней части неравенства:

Отсюда видно выражение для 100(1-α)% доверительного интервала для μ, рассчитываемое по набору наблюдений x₁...x_n при знании дисперсии σ²:

(1)

Напомним, что - это среднее, рассчитанное по имеющемуся набору наблюдений.

Заметим, что знание дисперсии при незнании математического ожидания – случай скорее удивительный, чем типичный, так что для практики гораздо более ценным представляется рассмотрение следующего случая.

Доверительный интервал для математического ожидания (μ) в случае нормальной генеральной совокупности и неизвестной дисперсии. Можно предположить, что в этом случае достаточно просто заменить в ранее полученном доверительном интервале истинное стандартное отклонение на рассчитанное по выборке. Этот подход не лишён смысла, однако стоит быть осторожнее. Дело в том, что если мы сделаем такую замену, то величина Z уже не будет распределена по стандартному нормальному закону.

Рассмотрим величину . Иначе её можно представить так:

Заметим, теперь в выражении есть истинная дисперсия наряду с выборочной. Выше уже говорилось, что и 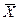независимы, а значит, независимы числитель и знаменатель этой дроби. В числителе стоит случайная величина, имеющая стандартное нормальное распределение, а в знаменателе – число 1/(n-1), умноженное на случайную величину, имеющую хи-квадрат распределение с (n-1) степенью свободы (см. распределение выборочной дисперсии). Таким образом, величина U имеет распределение Стьюдента с (n-1) степенью свободы.

Теперь нужно найти такое значение t, что P(|U|≥t)=α. Его обычно обозначают , потому что, в силу симметричности распределения Стьюдента, . Для нахождения этих чисел прекрасно подходят таблицы в учебнике А.С.Шведова. Например, при количестве степеней свободы, равном 14 (то есть, при 15 наблюдениях), и уровне доверия 95% (то есть, α=0,05) нужным нам значением будет =2,145. А при уровне доверия 90% и 19-и степенях свободы будет равно 1,729.

Далее поступаем аналогично предыдущему случаю.

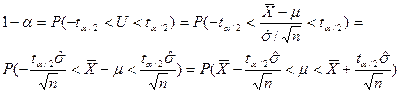
Таким образом, в случае неизвестной дисперсии 100(1-α)% доверительный интервал для математического ожидания имеет следующее выражение:

(2)

Учтем, что индекс α/2 при букве t – это не количество степеней свободы!!! Оно для переменной U будет равно n-1.

 

Творческое задание. Анализ статьи «Inflammation, Aspirin, and the Risk of Cardiovascular Disease in Apparently Healthy Men» [4,5]

 

Изучалось: увеличивает ли воспалительный процесс риск возникновения тромботических заболеваний; снижает ли приём аспирина этот риск.

Методика: авторы измерили уровень плазменного C-реактивного белка, маркер системного воспаления, у 543 здоровых мужчин, у которых впоследствии развился инфаркт миокарда, инсульт или венозный тромбоз, и у 543 участников исследования, которые не сообщили о сосудистых заболеваниях в течение последующего периода, превышающего восемь лет. Участники были рандомизированы для приёма аспирина или плацебо в начале исследования.

Перед рандомизацией в период с августа 1982 года по декабрь 1984 года потенциальным участникам было предложено предоставлять образцы опытной линии крови в течение 16-недельного периода, в течение которого всем участникам был дан аспирин, и никто не получал плацебо. Комплекты для сбора крови, включая трубки EDTA Vacutainer, были отправлены участникам с инструкциями по взятию крови. Участников попросили залить их кровь в трубки EDTA, центрифугировать трубки и вернуть плазму (в «холодном пакете», предоставленном участникам) ночным курьером. Затем образцы разделяли на аликвоты и хранили при −80°С. Из 22 071 участников 14 916 (68%) предоставили образцы «опытной» плазмы. В течение 14 лет испытания случайным образом допускалось таяние образцов.

Контроль был выбран случайным образом среди участников исследования, которые соответствовали критериям соответствия возраста (±1 год), статусу курения (курение в настоящее время, курили в прошлом или никогда не курили), а также продолжительность времени, прошедшего после после рандомизации (через 6-месячные интервалы). Используя эти методы, авторы оценили 543 пациента и 543 контроля.

Статистика. Для пациентов из контрольной группы были рассчитаны средние или доли для базовых факторов риска. Значение любой разницы в средних было проверено с использованием t -критерия Стьюдента, а значение любых различий в долях было проверено с использованием статистики χ². Поскольку значения С-реактивного белка искажены, вычислялись средние концентрации, и значение любых различий в средних значениях между пациентами и контрольной группой оценивали с использованием рангового теста Уилкоксона (будет рассмотрен далее). Геометрические средние концентрации С-реактивного белка также вычислялись после логарифмирования, что приводило к почти нормальному распределению. Авторы использовали тест для тренда, чтобы оценить любое соотношение возрастающих значений С-реактивного белка с риском будущего сосудистого заболевания после деления образца на квартили, определяемые распределением контрольных значений. Авторы получили скорректированные оценки с использованием условных моделей логистической регрессии, которые учитывали сопоставимые переменные и контролировали назначение случайного лечения, индекс массы тела, диабет, историю гипертонии и родительскую историю болезни коронарной артерии. Аналогичные модели использовались для корректировки измеренных концентраций общей массы и холестерина, ЛПВП, триглицеридов, липопротеинов, антигена t-PA, фибриногена, D-димера и гомоцистеина. Чтобы оценить, повлиял ли аспирин на эти отношения, анализы были повторены для всех случаев инфаркта миокарда, произошедшего 25 января 1988 года или до этого, — даты, когда рандомизированное назначение аспирина прекращалось.

Результаты. Средние и медианные концентрации плазмы C-реактивного белка у опытной линии были значительно выше среди тех, у кого впоследствии развилось любое сосудистое заболевание, чем у тех, у кого не развилось сосудистое заболевание (P = 0,001).

 

 

U -тест Манна — Уитни (Mann — Whitney U), также известный кактест Уилкоксона ранговых сумм (Wilcoxon Rank Sum) или тест Манна — Уитни — Уилкоксона (MWW) проверяет, являются ли две сравниваемые группы выборками из одного и того же распределения, используя в качестве статистики (U) медиану всевозможных разностей между элементами одной и второй выборки. По этой причине на результат практически не влияют редкие экстремальные значения. Для ранговых шкал, когда t -тест не применим, MWW-тест остаётся логичным выбором. Проблемы с интерпретацией теста, как и в случае t -тестов, возникают, когда распределения для двух выборок отличаются по форме, например, имеют сильно отличающиеся дисперсии.

Представление данных

Выборка 1 (объём n ₁): x ₁₁, x ₂₁, …, ;

Выборка 2 (объём n ₂): x ₁₂, x ₂₂, …, .

Наблюдения из двух выборок объёма n _1­ и n ₂объединяются и упорядочиваются, например, по возрастанию. Затем наблюдениям присваиваются ранги.

Выборка первая (объём п ₁)

Наблюдение x ₁₁, x ₂₁, …,

Ранг r ₁₁, r ₂₁, …,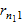

Сумма рангов в первой выборке

Выборка вторая (объём n ₂)

Наблюдение x ₁₂, x ₂₂, …,

Ранг r ₁₂, r ₂₂, …,

Сумма рангов во второй выборке

Общее число наблюдений N = n ₁+ n ₂.

Статистическая модель

Все наблюдения независимы. Наблюдения, входящих в одну выборку, относятся к одной совокупности.

Гипотезы

Н ₀: совокупности одинаково распределены;

Н ₁: нулевая гипотеза неверна

Критериальная статистика

Малые выборки

Вычисляются

и берётся

U = max(U ₁, U ₂).

Большие выборки

В том случае, когда объём меньшей выборки больше 20 или объём большей выборки превышает 40, то U распределение Манна — Уитни приближается к нормальному.

Пусть

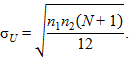
z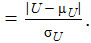

В том случае, если совпадающие ранги существуют, то

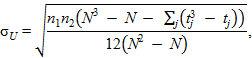
где j — число связок, t_j — число элементов в связке.

Поправка Йейтса:

z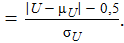

Отсутствие поправки на непрерывность приводит к увеличению значения статистики и, соответственно, уменьшению величины достигнутого уровня значимости. Это приводит к более частому отклонению нулевой гипотезы и принятию гипотезы Н ₁.

Результаты статьи. В статье были сравнены концентрации С-реактивного белка у двух групп мужчин (по 543 человека в каждой в соответствии, стало быть, указанного выше «рецепта» применения данного критерия). Точно проследить использование данного критерия не представляется возможным по данной статье, так как авторы не приводят первичные данные для 1086 участников.

Концентрации C-реактивных белков плазмы в «эксперименте» были выше среди мужчин, у которых был инфаркт миокарда (1,51 против 1,13 мг/л, P < 0,001) или ишемический инсульт (1,38 против 1,13 мг/л, P = 0,02), но не венозный тромбоз (1,26 против 1,13 мг на литр, P = 0,34), чем у мужчин без сосудистых событий. У мужчин в квартилях с самыми высокими значениями концентрации C-реактивного белка риск возникновения инфаркта миокарда в три (относительный риск, 2,9, P < 0,001) и риск возникновения ишемического инсульта (относительный риск 1,9; P = 0,02) в два раза превышал таковой у мужчин в наименьшей квартили. Риски были стабильными в течение длительного периода времени, их значения не были подвергнуты влиянию курению и не зависели от других факторов риска, связанных и не связанных с липидами. Использование аспирина было связано со значительным снижением риска инфаркта миокарда (снижение на 55,7%, P = = 0,02) среди мужчин в самом высоком квартиле, но с небольшими незначительными сокращениями среди низших квартилей (13,9%, P = 0,77).

Экспериментальная концентрации С-реактивного белка в плазме предсказывает риск будущего инфаркта миокарда и инсульта. Более того, снижение, связанное с использованием аспирина в риске развития первого инфаркта миокарда, по-видимому, напрямую связано с уровнем С-реактивного белка, повышая вероятность того, что противовоспалительные агенты могут иметь клинические преимущества в профилактике сердечно-сосудистых заболеваний.

 

 

Список использованной литературы:

1. Ивашёв-Мусатов О. С. Теория вероятностей и математическая статистика: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: ФИМА, 2003. — 224 с.

2. Гланц С. Медико-биологическая статистика. Пер. с англ. — М., Практика, 1998. — 459 с.

3. Кочнева Л.Ф., Липкина З.С., Новосельцева В. И. Теория вероятностей и математическая статистика (Часть III): Учеб. пособие - федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения», Москва, 2012. – 44с.

4. Ridker P. M. et al. Inflammation, aspirin, and the risk of cardiovascular disease in apparently healthy men //New England journal of medicine. — 1997. — V. 336. — N. 14. — Pp. 973-979.

5. Яровая Е. Б. Лекции курса основ теории вероятностей и математической статистики, прочитанные в МГУ имени М. В. Ломоносова на факультете фундаментальной медицины с 10.02.2017 по 18.05.2018.