Время выполнения алгоритмов обработки BST-деревьев зависит от форм деревьев. В лучшем случае дерево может быть полностью сбалансированным и содержать приблизительно lgN узлов между корнем и каждым из внешних узлов, но в худшем случае в каждый из путей поиска может содержать N узлов[3].
Можно также надеяться, что в среднем время поиска также будет связано с количеством узлов логарифмической зависимостью, поскольку первый вставляемый элемент становится корнем дерева. Если N ключей должны быть вставлены в произвольном порядке, то этот элемент делил бы ключи пополам (в среднем), что дало бы логарифмическую зависимость времени поиска (при использовании аналогичных рассуждений применительно к поддеревьям). Действительно, возможен случай, когда BST-дерево приводит в точности к тем же сравнениям, что и бинарный поиск. Этот случай был бы наилучшим для данного алгоритма, гарантируя логарифмическую зависимость времени выполнения для всех видов поиска. В действительно произвольной ситуации корнем может быть любой ключ, и поэтому полностью сбалансированные деревья встречаются исключительно редко, соответственно, без особых усилий не удастся сохранять дерево полностью сбалансированным после каждой вставки. Однако полностью несбалансированные деревья также встречаются редко при произвольных ключах, потому-то в среднем деревья достаточно хорошо сбалансированы. В этом разделе мы детализируем это наблюдение.
В частности, длина пути и высота бинарных деревьев, непосредственно связаны с затратами на поиск в BST-деревьях. Высота определяет стоимость поиска в худшем случае, длина внутреннего пути непосредственно связана со стоимостью попаданий при поиске, а длина внешнего пути непосредственно связана со стоимостью промахов при поиске.
Лемма 18: Для обнаружения попадания при поиске в дереве бинарного поиска, образованном N произвольными ключами, в среднем требуется около 2 lgN ~ 1.39 lgN сравнений.
Cчитаем последовательные операции == и < одной операцией сравнения. Количество сравнений, использованных для обнаружения попадания при поиске, завершающемся в данном узле, равно 1 плюс расстояние от этого узла до корня. Таким образом, интересующая величина равна 1 плюс средняя длина внутреннего пути BST-дерева, которую можно проанализировать с использованием уже знакомых рассуждений: если 
— средняя длина внутреннего пути BST-дерева, состоящего из N узлов, мы имеем следующее рекуррентное соотношение:
при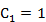 
. Член N-1 учитывает, что корень увеличивает длину пути для каждого из остальных N-1 узлов на 1; остальная часть выражения вытекает из того, что ключ в корне (вставленный первым) с равной вероятностью может быть к-м по величине ключом, разбивая дерево на произвольные поддеревья размерами &-1 и N - k.
Лемма 19: Для выполнения вставок и обнаружения промахов при поиске в дереве бинарного поиска, образованном N произвольными ключами, в среднем требуется около 2 lg N ~ 1.39 lgN сравнений.
Поиск произвольного ключа в дереве, содержащем N узлов, с равной вероятностью может завершиться в любом из N - 1 внешних узлов обнаружением промаха при поиске. Эта лемма в сочетании с тем, что разница длин внешнего и внутреннего пути в любом дереве равна просто 2 N), обусловливает оговоренный результат. В любом BST- дереве среднее количество сравнений, необходимых для выполнения вставки или обнаружения промаха, приблизительно на 1 больше среднего количества сравнений, необходимых для выявления попадания при поиске.
Рисунок 34. Пример дерева бинарного поиска
В этом BST-дepeвe, которое было построено за счет вставки около 200 произвольных ключей в первоначально пустое дерево, ни один поиск не использует более 12 сравнений. Средняя стоимость обнаружения попадания при поиске приблизительно равна 10.
В соответствии с леммой 18 следует ожидать, что затраты на поиск для BST-деревьев должна быть приблизительно на 39% выше затрат для бинарного поиска произвольных ключей. Но в соответствии с леммой 19 дополнительные затраты вполне окупаются, поскольку новый ключ может быть вставлен почти при тех же затратах — подобная гибкость при использовании бинарного поиска не доступна.
На рисунке 34 показано BST-дерево, полученное в результате длинной цепи произвольных перестановок. Хотя оно содержит несколько длинных и несколько коротких путей, его можно считать хорошо сбалансированным: для выполнения любого поиска требуется менее 12 сравнений, а среднее количество сравнений, необходимых для обнаружения произвольного попадания при поиске равно 7.00, что сравнимо с 5.74 для случая бинарного поиска.
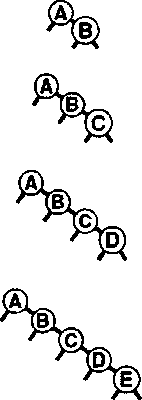
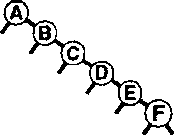
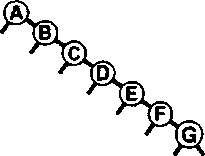
Рисунок.35. Худший случай дерева бинарного поиска
Если ключи в BST-дереве вставляются в порядке возрастания, дерево вырождается в форму, эквивалентную односвязному списку, приводя к квадратичной зависимости времени создания дерева и к линейной зависимости времени поиска.
Леммы 18 и 19 определяют производительность для среднего случая при условии, что порядок ключей произволен. Если это не так, производительность алгоритма имеет тенденцию к снижению.
Лемма 20: В худшем случае для поиска в дереве бинарного поиска с N ключами может требоваться N сравнений.
На рис. 35 показаны два примера наихудших случаев BST-деревьев. Для этих деревьев поиск с использованием бинарного дерева ничем не лучше последовательного поиска с использованием односвязных списков.
Таким образом, высокая производительность базовой реализации таблиц символов с использованием BST-дерева требует, чтобы ключи в достаточной степени были подобны произвольным ключам, а дерево не содержало длинных путей.
Более того, наихудший случай не столь уж редко встречается на практике — он возникает при вставке ключей в первоначально пустое дерево по порядку или в обратном порядке с применением стандартного алгоритма — последовательность операций, которую мы определено можем предпринять, не получив никакого явного предупреждения не делать этого. Ни одна из других рассмотренных реализаций таблиц символов не может использоваться для выполнения задачи вставки в таблицу очень большого количества произвольных ключей, а затем поиска каждого из них — время выполнения каждого из методов определяется квадратичной зависимостью. Более того, из анализа следует, что среднее расстояние до узла в бинарном дереве пропорционально логарифму количества узлов в дереве, что позволяет эффективно выполнять смешанные наборы операций поиска, вставки и других операций с АТД таблицы символов, что и будет вскоре показано.
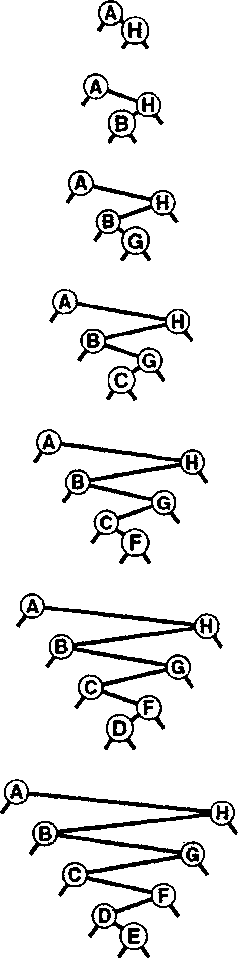
Рисунок 36. Ещё один худший случай дерева бинарного поиска.
Множество других подобных вариантов порядка вставки ключей приводят к вырождению BST-дерева. Тем не менее, дерево бинарного поиска, образованное произвольно упорядоченными ключами, скорее всего, окажется хорошо сбалансированным.