Вневписанная окружность. Опорные задачи

Вневписанная окружность и ее свойства.

Вневписанной окружностью называется окружность,касающаяся одной из сторон треугольника и продолжений двух других сторон. Центром вневписанной окружности является точка пересечения биссектрис внешних углов и биссектрисы внутреннего угла треугольника при третьей вершине.

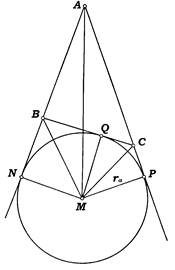
Рис. 1

Задача 1. Вычислите радиус вневписанной окружности, если известны площадь, полупериметр и сторона треугольника, которой касается эта окружность.

Решение. Пусть дан треугольник ABC, где BC=a, AC=b и AB=c. Точка M – центр вневписанной окружности, касающейся стороны a. Обозначим радиус вневписанной окружности через 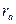. Чтобы вычислить радиус вневписанной окружности рассмотрим площади треугольников ABC, ABM, ACM, BCM (рис.1). Тогда

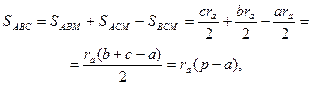
где p – полупериметр треугольника ABC. Следовательно,

.

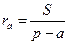(1)

Аналогично доказывается, что

.

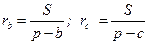(1')

Задача 2. Докажите, что отрезок от вершины треугольника до точки касания вневписанной окружности, расположенной на продолжении стороны, равен полупериметру.

Решение. Пусть дан треугольник ABC, где BC=a, AC=b и AB=c, N и P – точки касания вневписанной окружности с продолжениями сторон AB и AC (рис. 1). Тогда AN=AB+BN=c+BQ; AP=AC+CP=b+QC (BN=BQ, CP=QC, как отрезки касательных, проведенных из одной точки). Так как AN=AP, то 2AN=b+c+BQ+QC=b+c+a=2p. Следовательно, AN=p. Что и требовалось доказать.

Задача 3. Вписанная окружность треугольника ABC касается стороны BC в точке K, а вневписанная - в точке L. Докажите, что CK=BL=(a+b-c)/2, где a, b, c – длины сторон треугольника.

Решение. Пусть M и N – точки касания вписанной окружности со сторонами AB и AC (рис. 2).

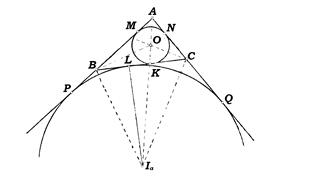
Рис. 2

Тогда BK+AN=BM+AM=AB, поэтому CK+CN=a+b-c. Пусть P и Q – точки касания вневписанной окружности с продолжениями сторон AB и AC (рис. 2). Тогда AP=AB+BP=AB+BL и AQ=AC+CQ=AC+CL. Поэтому AP+AQ=a+b+c. Следовательно, BL=BP=AP-AB=(a+b-c)/2.

Точка Нагеля. Прямые, соединяющие вершины треугольника с точками касания соответственных вневписанных окружностей, пересекаются в одной точке, называемой точкой Нагеля (рис.3).

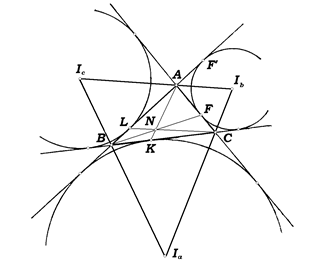
Рис. 3

Доказательство. Так как AF=AF’=BF’-BA=p-c, CK=p-b, BL=p-a, FC=p-a, KB=p-c, LA=p-b, то 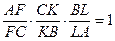(по теореме Чевы). Следовательно, прямые AK, BF и CL пересекаются в одной точке.

Задача 4. Доказать, что AP=BR, AN=CS и OB=CQ, где O, R, P, N, Q, S – точки касания вневписанных окружностей с продолжениями сторон треугольника ABC (рис. 4).

Решение.

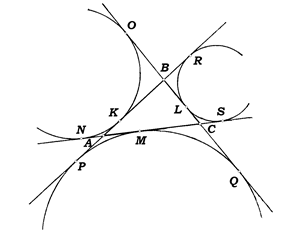
Рис. 4

Заметим, что NA=AK, AP=AM, CM=CQ, CS=CL, BL=BR, BK=OB (как отрезки касательных, проведенных из одной точки).

PA+AK+KB=BL+LC+CQ

и AK+KB+BR=AM+MC+CS

или

AP+AK+KB=BL+LC+CQ

и AK+KB+BR=AM+CL+CQ.

Вычтем из первого равенства второе. Получим: AP-BR=BL-AM или AP-BR=BR-AP. Следовательно, AP=BR. Аналогично доказывается, что AN=CS и OB=CQ.

Задача 5. Доказать следующие соотношения:

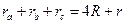
	(2)
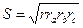
	(3)
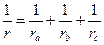
	(4)
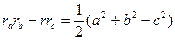
	(5)
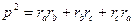
	(6)
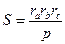
	(7)
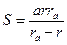
	(8)
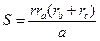
	(9)
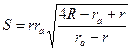
	(10)
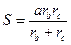
	(11)
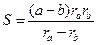
	(12)
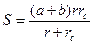
	(13)
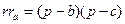
	(14)
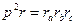
	(15)
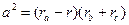
	(16)
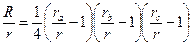
	(17)
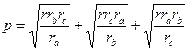
	(18)
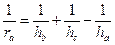
	(19)
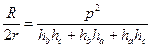
	(20)
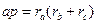
	(21)

Где: a, b и c – стороны треугольника;

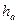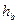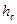, , - высоты, проведенные из вершин треугольника к сторонам a, b и c соответственно;

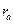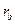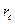, , - радиусы вневписанных окружностей, касающихся сторон a, b и c соответственно;

R – радиус описанной окружности;

r – радиус вписанной окружности;

S – площадь треугольника;

p – полупериметр треугольника.

 

 

Решение. Отметим, что для доказательства вышеперечисленных формул используются формулы (1) и (1').

1. Докажем формулу (2). Для этого применим формулу (1) .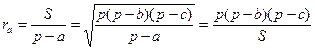

Аналогично: .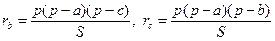

Известно, что 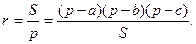Получаем:

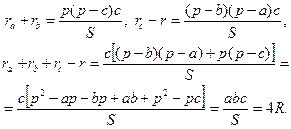
Что и требовалось доказать.

2. Докажем формулу (5).

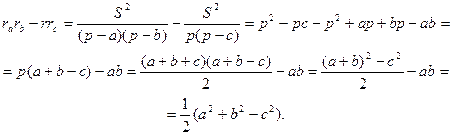
Следовательно, .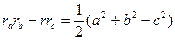

3. Докажем формулу (18).

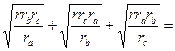
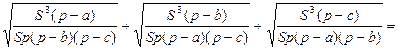
= p - a + p - b + p – c = 3 p - (a+b+c) = p. Что и требовалось доказать.

4. Докажем формулу (19).

Известно, что 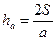, , 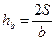, 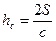тогда:

.

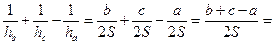
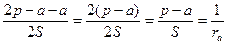Следовательно, .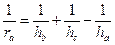

5. Докажем формулу (20)

.

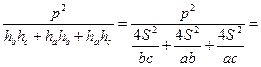
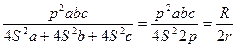Следовательно, .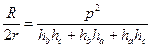

Остальные формулы доказываются аналогично.

Задача 6. Доказать, что в прямоугольном треугольнике с гипотенузой с .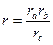

Решение. Было доказано, что в любом треугольнике 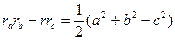(см. формулу (5)). Но в прямоугольном треугольнике с гипотенузой c a² + b² - c²=0 (теорема Пифагора). Следовательно, для прямоугольного треугольника верно равенство 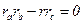. Тогда .

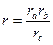Задача 7. Доказать, что в прямоугольном треугольнике с гипотенузой с .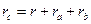

Решение. В прямоугольном треугольнике r = (a+b-c)/2=p-c. Используя формулы (1) и (1'), получаем:

;

;

;

; ; .

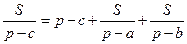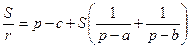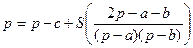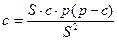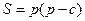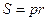Следовательно .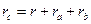

Задача 8. Доказать, что в прямоугольном треугольнике 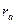и 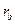являются корнями квадратного уравнения 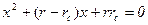или корнями уравнения .

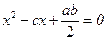Решение. По теореме Виета в уравнении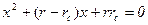

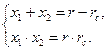
Пусть 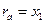, а 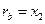. Тогда получим систему:

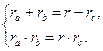
Оба уравнения верны для прямоугольного треугольника (см. задачи 7 и 8). По теореме Виета в уравнении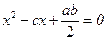

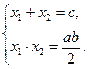
Пусть 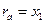, а 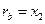. Тогда получим систему:

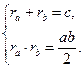
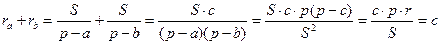. с=с. Следовательно, .

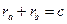Докажем, что 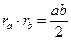. В прямоугольном треугольнике 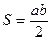; 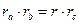, r=p-c, тогда 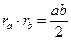(по формуле (1') 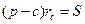). Следовательно, S=S. Следовательно, .

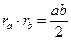Задача 9. Доказать следующие соотношения:

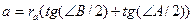
	(22)
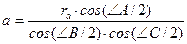
	(23)
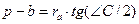
	(24)
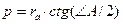
	(25)
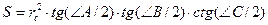
	(26)

Решение. Рассмотрим рис. 5: K – точка касания вневписанной окружности со стороной BC, L – с прямой AB; 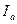- центр вневписанной окружности. BC=a, 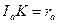, a=BK+KC, 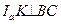(так как 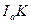проведен в точку касания вневписанной окружности).

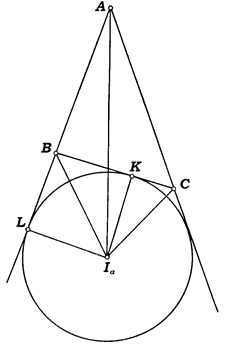
Рис. 5

 

 

1. Докажем формулу (22).

В прямоугольном треугольнике 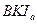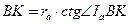. 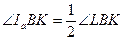(центр вневписанной окружности является точкой пересечения биссектрис). 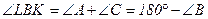. Следовательно, 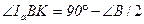. Тогда 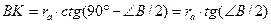. Что и требовалось доказать.

В прямоугольном треугольнике 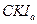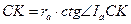. Аналогично доказывается, что . .

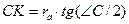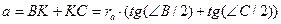2. Докажем формулу (23).

; .

; .

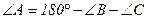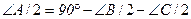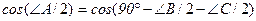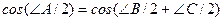Следовательно, .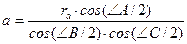

3. Докажем формулу (24).

Известно, что 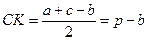(см. задачу 3). В прямоугольном треугольнике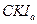 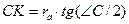(см. доказательство формулы (23)). Следовательно, .

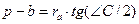4. Докажем формулу (25).

Рассмотрим треугольник 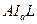: 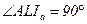( 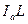проведен в точку касания вневписанной окружности). 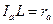, 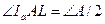(т. к. 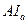- биссектриса).

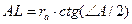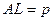; (см. задачу 2).

Следовательно, .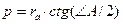

5. Докажем формулу (26).

Известно, что 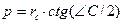(см. доказательство формулы (25)) и 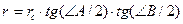. Перемножив эти равенства, получим:

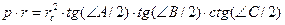, т. е. .

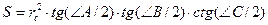Задача 10. Продолжение биссектрисы угла B треугольника ABC пересекают описанную окружность в точке M; O – центр вписанной окружности, - центр вневписанной окружности, касающейся стороны AC. Докажите, что точки A, C, O и лежат на окружности с центром в точке M (рис. 6).

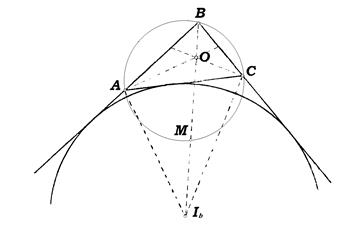
Рис. 6

Решение. Так как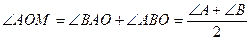

и 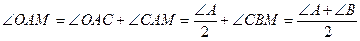, то MA=MO. Аналогично доказывается, что MC=MO. Так как треугольник 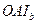прямоугольный и 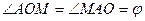, то 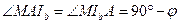, а значит, 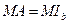. Аналогично доказывается, что .

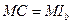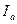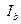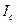Задача 11. Пусть , и - центры вневписанных окружностей треугольника ABC. Докажите, что точки A, B и C - основания высот треугольника 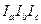(рис. 7).

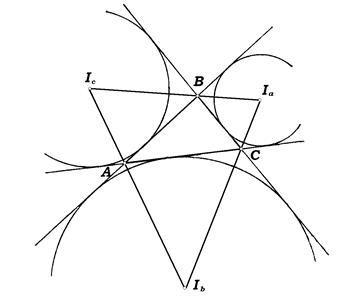
Рис. 7

Решение. Луч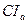и и 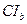- биссектрисы внешних углов треугольника при вершине C, поэтому C лежит на прямо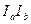й и 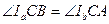. Так как 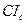- биссектриса угла BCA, то 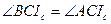. Складывая эти равенства, получаем 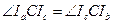, то есть 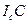- высота треугольника 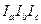. Аналогично доказывается, что 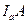и 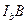- высоты этого треугольника.

Задача 12. Докажите, что сторона BC треугольника ABC видна из центра O вписанной окружности под углом 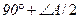, а из центра вневписанной окружности под углом .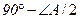

Решение. Ясно, что:

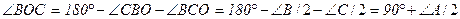, а , так как .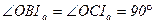

Задача 13. Вневписанная окружность треугольника АВС касается его стороны ВС в точке К, а продол­жения стороны АВ — в точке L. Другая вневписанная окружность касается продолжений сторон АВ и ВС в точках М и N соответст­венно. Докажите, что прямая KL параллельна, а прямая MN — перпендикулярна биссектрисе угла В треугольника (рис. 8).

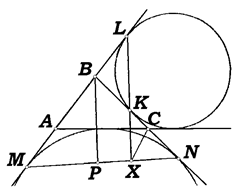
Рис. 8

Решение. Пусть P – точка пересечения биссектрисы угла B треугольника ABC и прямой MN. Рассмотрим треугольник BLK – равнобедренный, так как BL = BK (как отрезки касательных проведенных из одной точки). Следовательно, …………………………………………………………………………………………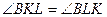

 

Различные задачи.

Задача 14. Пусть O - центр вписанной окружности треугольника ABC, I - центр описанной окружности, - центр вневписанной окружности, касающейся стороны BC. Докажите, что 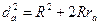, где .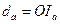

Решение. Пусть M - точка пересечения прямой 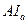с описанной окружностью. Тогда 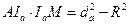. Так как 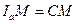(см. задачу 10), то 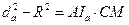. Остается заметить, что 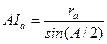и .

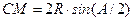Задача 15. В треугольнике ABC угол C прямой. Докажите, что 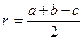и .

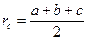Решение. Пусть вписанная окружность касается стороны AC в точке K, а вневписанная окружность касается продолжения стороны AC в точке L (рис. 2). Тогда r=CK и 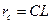. Остается воспользоваться результатом задачи 3.

Задача 16. Докажите, что описанная окружность треугольника ABC являются окружностью девяти точек для треугольника, образованного центрами вневписанных окружностей треугольника ABC.

Окружность девяти точек – окружность, на которой расположены середины сторон треугольника, основания высот и середины отрезков, соединяющих ортоцентр треугольника с вершинами.

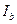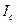Решение. Пусть , и - центры вневписанных окружностей треугольника ABC. Вершины треугольника ABC являются основаниями высот треугольника 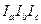(см. задачу 11), поэтому окружность девяти точек треугольника 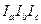проходит через точки A, B и C.

Задача 17. В треугольнике ABC угол A равен 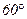; O - центр описанной окружности, H - ортоцентр, I - центр вписанной окружности, а - центр вневписанной окружности, касающейся стороны BC. Докажите, что IO=IH и 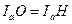(рис.8).

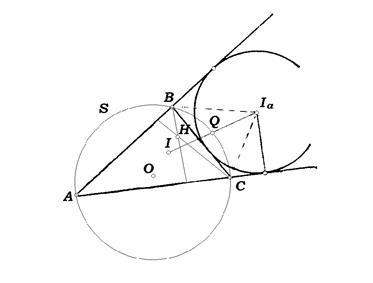
Рис. 9

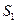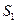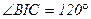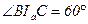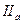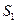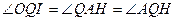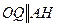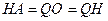Решение. Пусть S - описанная окружность треугольника ABC, Q - точка пересечения биссектрисы угла BAC с окружностью S. Легко проверить, что Q - центр окружности , симметричной окружности S относительно прямой BC. Кроме того, точки O и H лежат на окружности , а так как и (см. задачу 12), то - диаметр окружности . Ясно также, что , так как и . Поэтому точки O и H симметричны относительно прямой .

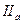Задача 18. Доказать, что во всяком треугольнике 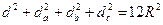, где d - расстояние между центрами описанного и вписанного кругов, 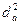, , 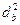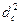- расстояния от центра описанного до соответственных центров вневписанных кругов.

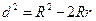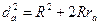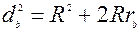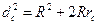Решение. Так как (по теореме Эйлера), , и (см. задачу 14), то, сложив эти равенства почленно и воспользовавшись формулой (2), получим: 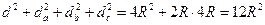. Что и требовалось доказать.

Задача 19. Из точки A проведены прямые, касающиеся окружности S в точках B и C. Докажите, что центр вписанной окружности треугольника ABC и центр его вписанной окружности, касающейся стороны BC, лежат на окружности S.

Решение. Пусть O - середина дуги окружности S, лежащей внутри треугольника ABC. Тогда 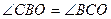, а по свойству угла между касательной и хордой 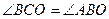. Поэтому BO - биссектриса угла ABC, то есть O - центр вписанной окружности треугольника ABC. Аналогично доказывается, что середина дуги окружности S, лежащей вне треугольника ABC, является центром его вневписанной окружности.

Задача 20. Доказать, что окружность девяти точек касается внешним образом каждой из вневписанных окружностей.

Решение. Опустим из 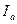(рис. 11) – центра вневписанной окружности – перпендикуляр 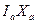на сторону BC треугольника ABC. Точки X и 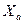равноудалены от 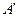- середины BC.

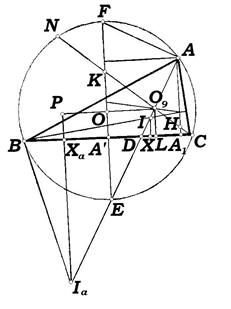
Рис. 10

Действительно, 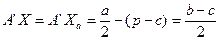. Треугольники AKF и 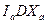подобны, так как их соответственные стороны взаимно перпендикулярны. Следовательно, 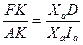, или 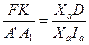. Отсюда

.

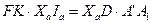(27)

В [2] доказывается, что

.

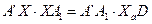(28)

Учитывая, что треугольник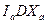и и 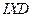подобны, преобразуем равенство (28), а затем и равенство (27):

,
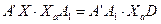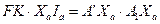.	(29)

Опустив из 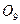перпендикуляр на 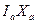, получим:

,

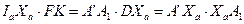(30)

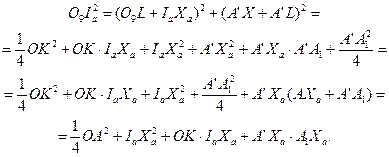
На основании равенства (29) имеем:

,

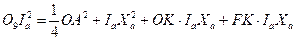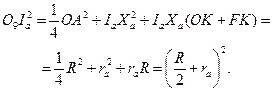
Следовательно,

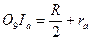
(31)

Из равенства (31) заключаем, что окружность девяти точек внешне касается вневписанной окружности.

Задача 21. Вневписанная окружность треугольника АВС касается его стороны ВС в точке К, а продол­жения стороны АВ — в точке L. Другая вневписанная окружность касается продолжений сторон АВ и ВС в точках М и N соответст­венно. Прямые KL и MN пересе­каются в точке X. Докажите, что СХ — биссектриса угла ACN (рис. 12) .

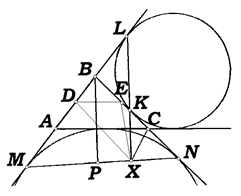
Рис. 11

Решение. Так как прямая KL параллельна, а прямая MN — перпендикулярна биссектрисе угла В треугольника (см. задачу 13), то MXL = 90°. Обозначим длины стороны треугольника: а = ВС, b = АС. Как известно, расстояния AL и ВМ равны полупериметру треугольника (см задачу 2). Отсюда следует, что ML = AL + BM - AB = a + b, и середина ML совпадает с середи­ной АВ. Пусть D - середина AB (и ML), Е — середина АС. Так как XD - медиана прямоугольного треугольника MXL, получаем, что XD = 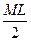= 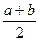и Ð MDX = 2ÐMLX = ÐABC (последнее ра­венство следует из того, что прямая LX параллельна биссектрисе угла АВС). Так как Ð MDX = Ð АВС, прямая DX параллельна сто­роне ВС и, следовательно, содержит среднюю линию DE. Значит, EX=DX-DE= 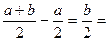ЕС, то есть треугольник ХЕС — равнобедренный. Так как ЕХ çç ВС, имеем Ð СЕХ = Ð АСВ, отку­да Ð ECX = 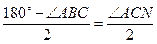, что и требовалось доказать.

Задача 22. К вневписанной окружности треугольника ABC, центр которой находится в точке 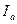, проведена касательная, параллельная BC. Найти длину отрезка этой касательной, содержащегося внутри угла A, если , , .

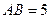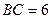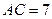Решение. Пусть DE - отрезок данной касательной, содержащийся внутри угла A. Вневписанная окружность с центром 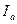и радиусом 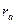является вписанной в треугольник ADE, подобный треугольнику ABC (рис. 13).

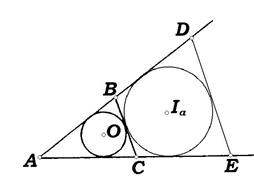
Рис. 12

 

Пусть r - радиус вписанной в треугольник ABC окружности. Тогда

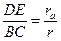, или .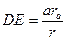

Для нахождения радиусов найдем сначала S треугольника ABC. Имеем:

, , , ,

; .

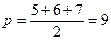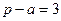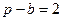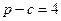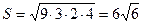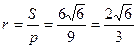Далее по формуле (1) получаем:

.

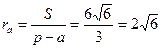Окончательно .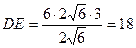

Ответ: длина отрезка касательной равна 18.

 

Задача 23. В треугольнике ABC стороны равны 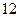, 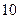и 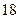. Найти радиусы вневписанных окружностей.

Решение. По формулам (1) и (1')

, , .

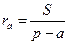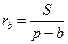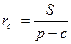Для нахождения радиусов найдем сначала S и p треугольника ABC.

, , , ;

.

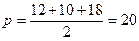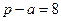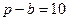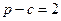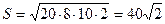Окончательно , , .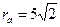

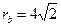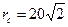Ответ: ; ; .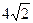

 

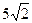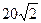Задача 24. Из четырех окружностей, касающихся сторон треугольника ABC (одной вписанной и трех вневписанных), рассмотрим те две, которые касаются стороны AB (точки касания располагаются между вершинами A и B). Доказать, что среднее геометрическое радиусов этих окружностей не превосходит половины длины стороны AB.

Решение. Пусть c - длина стороны AB треугольника ABC, r - радиус вписанной окружности, 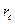- радиус вневписанной окружности, касающейся стороны AB и продолжений сторон треугольника ABC, S - площадь треугольника ABC, p - его полупериметр. Воспользуемся соотношением (1'):

, .

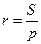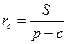Тогда

,

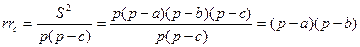следовательно, .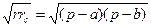

Поскольку среднее геометрическое двух положительных чисел никогда не превышает их среднего арифметического, то

,

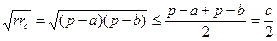что и требовалось доказать.

 

Литература:

1. Моденов П.С. Сборник задач по специальному курсу элементарной математики. М: изд. Советская наука, 1957. с. 662.

2. Зетель С.И. Новая геометрия треугольника, М.: учпедгиз, 1962. - 152 с.

3. Прасолов В.В. Задачи по планиметрии. Ч. 1. – 2-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ. – мат. лит., 1991. – 320 с. – (Б-ка мат. кружка. Вып. 15).

4. Зив Б.Г. Задачи к урокам геометрии. 7-11 классы. – С. – Петербург, 1988. НПО «Мир и семья-95» - 624 с.: илл.

5. Адамар Ж. Элементарная геометрия, часть первая, планиметрия, государственное учебно-педагогическое издательство наркомпроса РСФСР. Москва. 1938.

6. Задачи Санкт – Петербургской олимпиады школьников по математике /С.Л. Верлов, С.В. Иванов и др./ Изд-во С. – Петербургского университета; С. – П.; 2000 г., 108 с.

7. Берже М. Геометрия: Пер с франц. – М.: Мир, 1984. – Т. 1. – 560 с., ил.

8. Кюршак Й., Нейкомм Д., Хайош Д., Шурани Я., Венгерские математические олимпиады. М., «Мир», 1976.

9. Математический энциклопедический словарь. – м.: Сов. энциклопедия, 1988. – 847 с.: ил.

10. Никулин А.В. и др. Планиметрия. Геометрия на плоскости: Уч. Пос./ Под общ. Ред. Ю.С. Татаренко. – Висагинас: Альфа, 1998. – 592 с. – (Библиотека школьника).

11. Новые встречи с геометрией (Серия: “Библиотека математического кружка”) М., 1978 г., 224 стр. с ил.

12. Цыпкин А.Г. Справочник по математике для средних учебных заведений. – 4-е изд.– М.; Наука. Гл. ред. физ. – мат. лит., 1988. – 432 с.

13. Энциклопедический словарь юного математика./ Сост. Э-68 А.П. Савин. – М.: Педагогика, 1989. – 352 с.: ил.

14. Энциклопедия для детей, т. 11, Математика, Аванта+, 1998 г.; 688 с., илл.

15. Яглом И.М., окружности, Энциклопедия элементарной математики, кн. 4, М., Физматгиз, 1963.