Пусть дано комплексное число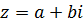 
. Из DOMA (см.рис.1) можно выразить действительные числа a и b через модуль r и аргумент j числа z следующим образом: 
, 
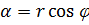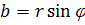. Таким образом, комплексное число можно записать в виде
),
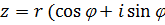Где r – модуль комплексного числа, а j - один из его аргументов. Представление комплексного числа z¹0 в указанном виде называется тригонометрической формой записи комплексного числа.
Для того чтобы перейти от алгебраической формы записи комплексного числа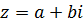
к тригонометрической, достаточно найти его модуль и один из аргументов. Аргумент комплексного числа 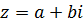можно находить и из системы 
.
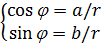Пример 5. Записать число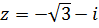 
в тригонометрической форме.
Решение. Находим модуль
Находим угол.
Вектор, соответствующий данному комплексному числу, лежит в ।।। координатной четверти (рис.4) поэтому одним из аргументов является 
.
Следовательно,
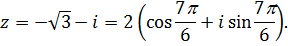
Для того чтобы перейти от тригонометрической формы записи комплексного числа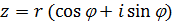 
к алгебраической, достаточно найти действительные числа a и b по формулам 
, .
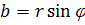Пример 6. Записать число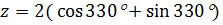 
в алгебраической форме.
Решение. Сначала найдем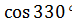 
и 
:
;
.
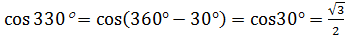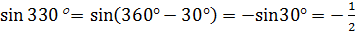Тогда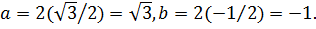 
Следовательно,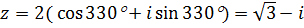 
.
Действия над комплексными числами, заданными в тригонометрической форме.
Если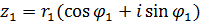 
и 
, то
,
Если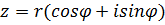 
, то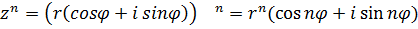 
,
Пример 7. Даны комплексные числа 
и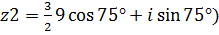 
. Найти их произведение z1/z2. Ответ записать в алгебраической форме.
Решение. Применяя правила умножения и деления комплексных чисел, имеем
;
.
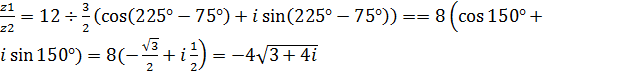Показательная форма комплексного числа. Рассматривая функцию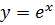 
для комплексного переменного, Эйлер установил замечательное соотношение
.
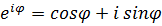Которое называется формулой Эйлера.
Из этой формулы следует, что каждое комплексное число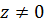 
можно записать в форме
,
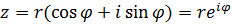Которая называется показательной формой записи.
Над комплексными числами, заданными в показательной форме, удобно производить умножение и деление, возведение в натуральную степень и извлечение корня:
;
;
;
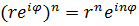Вопросы и упражнения для самопроверки
1. Дайте определение комплексного числа.
2. Дайте определение мнимой единицы.
3. Как найти степень мнимой единицы?
4. Какие комплексные числа называют равными; сопряженными?
5. Как изображаются комплексные числа геометрически?
6. Дайте определение модуля и аргумента комплексного числа.
7. Перечислите формы записи комплексного числа.
8. Как выполняются действия над комплексными числами, заданными в алгебраической форме; в показательной форме?
Производная
Производная. Понятие производной является одним из фундаментальных понятий математики. Многие как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция y=f(x) определена в промежутке Х. Возьмем из этого промежутка фиксированное значение аргумента х и придадим ему приращение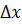 
так, чтобы новое значение аргумента 
принадлежало этому промежутку. Тогда значение функции f(x) заменится новым значением f(x)+ 
=f(x+ 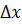), т. е функция получит приращение 
.
Предел отношения приращения функции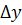 
к вызвавшему его приращению аргумента 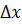при стремлении 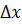к нулю, т. е.
,
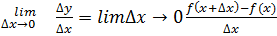Называется производной функции y=f(x) по аргументу х в точке х.
Производная обозначается одним из символов: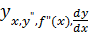 
, а ее значения при x=x0 обозначается 
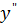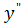(x0), 
(x0)
Операция нахождения производной называется дифференцированием.
Если функция f(x) имеет производную в точке х, то она называется дифференцируемой в этой точке.
Если функция f(x) имеет производную в каждой точке промежутка Х, то говорят, что эта функция дифференцируема на этом промежутке.
Производная сложной функции:
Пусть y=f(u), где u является не независимой переменной, а функцией независимой переменной х: u = j (х). Таким образом, y = f (j (х)).
В этом случае, функция y называется сложной функцией х, а переменная u – промежуточным аргументом.
производная сложной функции находится на основании следующей теоремы:
если y=f (u) и u=j (x) – дифференцируемые функции своих аргументов, то производная сложной функции y = f (j (x)) существует и равна произведению производной функции у по промежуточному аргументу и на производную промежуточного аргумента по независимой переменной х:
Эта теорема распространяется на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например, если y=f (u), u=j (u), u= Y (x), т.е. y=f (j (Y (x))), то 
.