Рассмотрим консольную балку, нагруженную распределенной нагрузкой интенсивностью q (рис. 5).
Поперечная сила в сечении z равна Q = + q · z, момент
равномерно
изгибающий
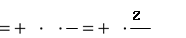M q z
z
2 q 2.
Y
q Z
а)
б) Q
в) M X
Рис. 5
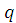В соответствии с геометрической интерпретацией первой про-изводной тангенс угла наклона касательной к эпюре перерезывающих сил Q равен интенсивности распределенной нагрузки в этом сечении. Очевидно, аналогичное утверждение справедливо и для эпюры M, только в этом случае тангенс угла наклона касательной к эпюре M равен Q в соответствующем сечении, т. е.
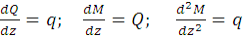. (1)
Из первых двух зависимостей следует: в сечениях, где q = 0, поперечная сила Q экстремальна; где Q = 0, изгибающий момент M экстремален.
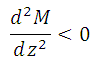
В приведенных дифференциальных зависимостях интенсив-ность распределенной нагрузки q положительна, если последняя действует вверх, а для Q и M справедливо принятое ранее правило знаков.
Поскольку вторая производная определяет знак кривизны кри-вой, то при принятом правиле знаков справедливо так называемое правило «дождя» или правило «зонтика». Суть этих правил заклю-чается в том, что выпуклость эпюры M всегда направлена навстречу распределенной нагрузке. Символично это правило представлено на рис. 6.
q < 0 q > 0
Эпюра M Эпюра M
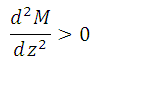
Рис. 6
Следует отметить, что приведенное правило справедливо только для изгибающего момента. Дифференциальные зависимости используются для проверки правильности построения эпюр, а также при построении эпюр по площадям.
Из дифференциальных зависимостей (1) и понятий о попереч-ной силе и изгибающем моменте можно сделать следующие выводы:
|
|
1. На участках балки, где Q > 0, изгибающий момент возрастает, там, где Q < 0, момент убывает.
2. В сечении, где Q при постоянном изменении обращается в нуль, изгибающий момент имеет экстремальное значение.
3. На том участке, где Q = 0, на эпюре М будет горизонтальная линия (прямая нулевого порядка), т. е. М = const (случай чистого изгиба).
4. При М = 0 изгиба нет, данный участок балки остается прямым, хотя и может изменить свое положение (переместиться) на плоскости.
5. На участке, где отсутствует распределенная нагрузка (q = 0), поперечная сила постоянна, т. е. эпюра Q представляет собой прямую, параллельную оси балки (прямая нулевого порядка), а эпюра M – наклонную прямую (прямая первого порядка).
6. На участке, загруженном равномерно распределенной нагрузкой (линия нулевого порядка), эпюра Q представляет собой прямую первого порядка, а эпюра М – дугу квадратной параболы (линия второго порядка).
Если при этом q действует сверху вниз, то при движении по эпюре слева направо линия эпюры Q направлена вниз; если q действует снизу вверх, линия эпюры Q направлена вверх.
Если линия эпюры Q пересекает горизонтальную ось по нисходящей прямой, то на эпюре М имеется максимум, а если по восходящей – минимум.
7. В сечении, где приложена сосредоточенная сила, на эпюре Q имеет место скачок на величину этой силы и направленный в сторону действия силы. На эпюре M в этом сечении должен быть перелом.
8. В сечении, где приложен сосредоточенный момент (пара сил) на эпюре M имеет место скачок на величину этого момента в направлении, соответствующем правилу знаков для моментов слева от сечения. Значение поперечной силы в этом сечении не изменяется.
|
|
9. На участке, загруженном треугольной нагрузкой (линия пер-вого порядка), на эпюре Q – кривая второго порядка, на эпюре M – третьего.
10. В концевых сечениях балки поперечная сила и изгибающий момент равны соответственно приложенным в этих сечениях сосре-доточенной силе и моменту пары.
11. Пересечение эпюрой Q горизонтальной оси с переходом с плюса на минус дает на эпюре M максимум, а с минуса на плюс – минимум.
Домашнее задание: напишите конспект