Пример задачи на использование 4 замечательных точек треугольника

Точка пересечения медиан треугольника

Теорема 1. О пересечении медиан треугольника:

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1 начиная с вершины.

Доказательство: Рассмотрим треугольник ABC, где AA1, BB1, CC1 его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию A1B1 (Рис. 1).

Рисунок 1.

Медианы треугольника По теореме 1, AB||A1B1 и AB=2A1B1, следовательно, ∠ABB1=∠BB1A1, ∠BAA1=∠AA1B1. Значит треугольники ABM и A1B1M подобны по первому признаку подобия треугольников. Теорема доказана.

Точка пересечения биссектрис треугольника

Теорема 2. О пересечении биссектрис треугольника.

Биссектрисы треугольника пересекаются в одной точке.

Доказательство. Рассмотрим треугольник ABC, где AM, BP, CK его биссектрисы. Пусть точка O - точка пересечения биссектрис и AM и BP. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

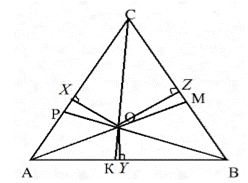
Рисунок 2. Биссектрисы треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 3. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. По теореме 3, имеем: OX=OZ, OX=OY. Следовательно, OY=OZ. Значит точка O равноудалена от сторон угла ACB и, значит, лежит на его биссектрисе CK. Теорема доказана.

Точка пересечения серединных перпендикуляров треугольника

Теорема 4. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство: Пусть дан треугольник ABC, n, m, p его серединные перпендикуляры. Пусть точка O - точка пересечения серединных перпендикуляров и n и m (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 5 Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: OB=OC, OB=OA. Следовательно, OA=OC. Значит точка O равноудалена от концов отрезка AC и, значит, лежит на его серединном перпендикуляре p. Теорема доказана.

Точка пересечения высот треугольника

Теорема 6 Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство: Рассмотрим треугольник ABC, где AA1, BB1, CC1 его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник A2B2C2 (рис. 4).

Рисунок 4. Высоты треугольника

Так как AC2BC и B2ABC параллелограммы с общей стороной, то AC2=AB2, то есть точка A -- середина стороны C2B2. Аналогично, получаем, что точка B -- середина стороны C2A2, а точка C -- середина стороны A2B2. Из построения мы имеем, что CC1⊥A2B2, BB1⊥A2C2, AA1⊥C2B2. Следовательно, AA1, BB1, CC1 -- серединные перпендикуляры треугольника A2B2C2. Тогда, по теореме 4, имеем, что высоты AA1, BB1, CC1 пересекаются в одной точке. Теорема доказана.

Пример задачи на использование 4 замечательных точек треугольника

Пример 1 Серединные перпендикуляры к сторонам AB и AC треугольника ABC пересекаются в точке D стороны BC. Докажите, что а) точка D -- середина стороны BC. б) ∠A=∠B+∠C Решение. Изобразим рисунок.

Рисунок 5.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке D. Следовательно, D - основание серединного перпендикуляра к стороне BC. Значит точка D -- середина стороны BC. б) Так как X и D -- середины сторон, то XD -- средняя линия треугольника. Тогда, по теореме о средней линии треугольника XD||AC. Значит,∠A=∠DXB, как соответственные углы. Значит, ∠A=90⁰. Тогда∠B+∠C=180⁰−∠A=180⁰−90⁰=90⁰=∠A ч. т. д.

В классной работе необходимо разобрать изучить п.74-76, записать в тетрадь доказательство теорем с видеоролика, решить № 674, 676 (а).

Домашнее задание: 676 (б).

Желаю успехов!!! Будьте здоровы!!!