VECM представляет собой аналог модели корректировки отклонений, использование которого основано на VAR-подходе
Известия Челябинского научного центра, вып. 2 (44), 2009
ЭКОНОМИКА И МЕНЕДЖМЕНТ
УДК 681.5:311, 681.5:338
ОБ ЭФФЕКТИВНОСТИ МОДЕЛИ ARIMA
ПРИ ПРОГНОЗИРОВАНИИ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ
В. Н. Анисимов, К. Л. Соломахо
∗
e-mail: solomahok@mail.ru
Южно-Уральский государственный университет, проспект им. В. И. Ленина, 76,
г. Челябинск, 454080, Россия
Статья поступила 26 февраля 2009 г.
Введение
Прогнозирование продаж ― одна из наиболее актуальных задач в торговле. Наличие про-
гноза позволяет производить закупки в нужном объеме и в нужное время. Благодаря этому уве-
личивается удовлетворенность клиентов, увеличивается оборачиваемость товаров, снижаются
требования к размеру складских помещений, уменьшаются риски образования нераспроданных
товаров.
Исходными данными при решении задачи прогнозирования являются динамические ряды,
анализ которых можно эффективно выполнить с помощью модели ARIMA. Методология Вокса-
Дженинкса подбора АRIMA-модели для временного ряда состоит из трех шагов. На первом ша-
ге строится стационарный ряд. Для идентификации в процессе построения стационарного вре-
менного ряда используются функция автокорреляции (AСF) и частная функция автокорреляции
(РАСF). Временной ряд тестируется на стационарность с помощью визуального анализа АСF
и РАСF, тесты на единичные корни. Если получается стационарный ряд, то осуществляется
переход к следующему шагу, если нет, то применяется оператор интегрирования (взятия по-
следовательной разности) и повторяется тестирование. На практике последовательная раз-
ность берется, как правило, не более двух раз. После того как получен стационарный времен-
ной ряд, формулируются предположения о возможных порядках авторегрессии и скользящего
среднего [1]. Обычно рекомендуется использовать модели возможно более низкого порядка.
Для каждой из выбранных на первом шаге моделей оцениваются их параметры и вычисляются
остатки. Каждая из моделей проверяется, насколько она соответствует данным. Из моделей,
адекватных данным, выбирается самая простая модель, т. е. модель с наименьшим количест-
вом параметров. После того как выбрана модель, выполняется прогноз за один или несколько
шагов по времени и оцениваются доверительные границы прогнозных значений.
Целью данной статьи является оценка эффективности метода ARIMA при решении задачи
прогнозирования продаж торгово-промышленных предприятий. В качестве пробного примера
для проверки правильности разработанной методики прогнозирования было решено выбрать
данные по месячным перевозкам авиапассажиров, имеющиеся в пакете STATISTICA [2].
∗
Анисимов Виктор Николаевич ― доцент, преподаватель, кандидат технических наук.
Соломахо Ксения Львовна ― аспирант кафедры ЭиП, solomahok@mail.ruОб эффективности модели ARIMA при прогнозировании экономических процессов 45
1. Прогнозирование авиаперевозок пассажиров
Данные (рис. 1) по месячным перевозкам авиапассажиров соответствуют периоду с января
1949 г. по декабрь 1960, т. е. за 12 лет. Из графика легко обнаружить сезонную составляющую ―
видно, что через каждые 12 месяцев форма кривой в большой степени повторяется. Для ис-
ключения сезонной составляющей заменим величины наблюдений на их разности, но не в со-
седних наблюдениях, а в наблюдениях, отстоящих друг от друга на 12 лагов, т. е. на один год.
Естественно, что в этом случае количество наблюдений уменьшается на 12 значений ― только
начиная с 13-го наблюдения можно получить такие разности. Следующим действием на пути
создания ARIMA-модели является определение порядка авторегрессионной модели и модели
скользящего среднего. Решить такую задачу можно с помощью графиков автокорреляционной
(АКФ) и частной автокорреляционной функции (ЧАКФ). Последние можно получить в любом
статистическом пакете или в системе MATLAB. Удобнее всего графики функций рассчитать
в Excel c помощью специальной надстройки.
Рис. 1. Месячные перевозки авиапассажиров
По виду графиков АСF и РАСF можно признать модель для ряда чисто авторегрессионной,
а ее порядок, равным двум или трем (в соответствии с количеством выбросов РАСF за пределы
границ белого шума). Результаты, полученные для p = 2, позволяют практически признать за-
дачу по стационаризации временного ряда решенной ― лишь один выброс в очень небольшой
степени выходит за границу белого шума.
К недостаткам надстройки следует отнести, во-первых, слишком короткую величину прогно-
за ― всего лишь на 1 лаг. На рис. 2 показано, как выглядит прогноз. Во-вторых, порядок моде-
лей, входящих в ARIMA, не может превышать 5-ти. И, наконец, в-третьих, прогноз выдается
в виде точечной, а не интервальной оценки. На основании вышеперечисленного было решено
находить коэффциенты регрессии и выполнять прогноз в Excel без использования рассмотрен-
ной выше надстройки.
Коэффициенты регрессии были рассчитаны в среде Excel с помощью надстройки «Анализ
данных» (Регрессия) [1]. Коэффициенты регрессии, полученные с помощью метода наимень-
ших квадратов (МНК), несколько отличаются (рис. 2) от найденных с помощью надстройки
«ARIMA». Даже при обнулении константы в уравнении регрессии совпадения между ними не
получилось. При этом проверка показала, что коэффициенты, найденные с помощью МНК,
обеспечивают получение меньшей суммы квадратов отклонений расчетных значений зависи-
мой переменной от фактических.
Количество перевезенных пассажиров с 01.1949 г. по 12. 1959 г.
Количество 46 В. Н. Анисимов, К. Л. Соломахо
Рис. 2. Решение задачи прогнозирования в рассматриваемом тестовом примере
В итоге построена модель ARIMA(2,1,0), а уравнение регрессии получилось следующим:
,
t tt
y yy
−
′ = −
t ttt
6,7383 0,5837 0.2118, 1 2
y yy e − −
′ ′ ′ = + + + 15,16 144. t = ÷
Рис. 3. Результаты передачи уровня регрессии в надстройку «ARIMA»
На рис. 3 показано, как отреагировала надстройка ARIMA, когда остатки t
e уравнения рег-
рессии были переданы в нее ― ряд признан чистым белым шумом при отсутствии внутренних
корреляций.
Знание интервальных оценок коэффициентов регрессии (например, для 5 %-го уровня зна-
чимости) позволяет получить интервальную оценку прогноза. На рис. 4 показан интервальный
прогноз на 12 месяцев вперед. Об эффективности модели ARIMA при прогнозировании экономических процессов 47
Рис. 4. Результаты прогнозирования на 12 месяцев вперед
2. Прогнозирование продаж в розничной торговле
Рис. 5. Начальный этап анализа реального временного ряда
После успешного решения пробного примера приступим к решению основной задачи ―
проанализируем временной ряд, представляющий собой изменение суммы продаж по дням
розничного предприятия в течение 363 дней. Из рис. 5 видно, что исходный ряд более сложен
по сравнению с предыдущим, количество выбросов ЧАКФ достигает 10. Выбор 10-го порядка
авторегрессионной модели не привел к положительному результату. Однако повышение поряд-
ка до 11-го оказалось достаточным.
Остатки, полученные после построения уравнения регрессии, оказались чистым белым
шумом. Таким образом, построена чистая авторегрессионная модель или модель,
ARIMA(11,0,0). коэффициенты. К сожалению, практическая ценность такого уравнения вызыва-
ет сомнение. Использование его для интервального (95%-го) прогноза на месяц вперед показы-
вает (см. рис. 6), что сумма продаж по этому товару может, по сравнению с существующей,
уменьшиться до нуля и возрасти в два раза. 48 В. Н. Анисимов, К. Л. Соломахо
Рис. 6. Результаты прогнозирования на 30 дней
Естественно, что такой прогноз никого удовлетворить не может. Иначе говоря, исследуе-
мый временной ряд не имеет какой-либо логики, которую можно было бы обнаружить с помо-
щью ARIMA-моделирования.
Заключение
В настоящее время, когда лицензионные специализированные пакеты, в частности
статистические или MATLAB, достаточно дороги, актуальными являются надстройки,
расширяющие возможности офисных программ, а именно табличного процессора Excel.
До недавнего времени задачу анализа временных рядов на основе модели ARIMA нельзя
было решить в среде Excel в интерактивном режиме. Авторам удалось найти надстройку
«ARIMA-3», позволяющую устранить этот пробел системы Excel. Надстройка, однако, оказалась
не без недостатков. Это было показано на примере решения тестового примера из пакета
STATISTICA (данные по месячным перевозкам авиапассажиров). Так, прогноз, который может
быть только точечным, выдается только на величину 1-го лага. Порядок авторегрессионной
модели и модели скользящего среднего не может превышать пяти. Для устранения
ограничения в рассматриваемой надстройке «ARIMA-3», была использована надстройка
«Регрессия», которая реализует для этих целей метод наименьших квадратов. Это позволило
расчитать интервальный прогноз, и не на один месяц, а на 12 месяцев. Так данные имеют
сезонную компоненту, расчеты велись на 12 месяцев ― на велечину сезона.
Прогнозирование с помощью метода ARIMA было продемонстрировано на двух задачах.
Для задачи прогнозирования авиаперевозок пассажиров модель ARIMA показала хорошие про-
гностические способности. Для задачи прогнозирования продаж товара розничным предприяти-
ем с помощью модели ARIMA получить практически значимого результата не удалось. Это по-
казывает, что для составления прогноза данный метод не всегда является подходящим.
Работа выполнена при финансовой поддержке фонда РГНФ (проект 08-02-85209а/У).
Список литературы
1. Варюхин С. Е. Примеры использования дополнительных надстроек MS Excel. Анализ временных ря-
дов с помощью надстройки «ARIMA». Академия народного хозяйства при правительстве РФ. ― Мо-
сква: Институт Бизнеса и Делового Администрирования, 2007. ― 14 с.
2. Боровиков В. П., Иванченко Г. И. Прогнозирование в системе STATISTICA в среде WINDOWS. ― Мо-
сква: Финансы и статистика, 2000. ― 380 с.
| ДонНТУ | Портал магистров
|
| Методология прогнозирования Бокса-Дженкинса
| | | Модели ARIMA опираются, в основном, на автокорреляционную структуру данных. В методологии ARIMA не предусматривается какой-либо четкой модели для прогнозирования данного временного ряда. Задается лишь общий класс моделей, которые описывают временной ряд и, которые позволяют как-то выражать текущее значение переменной через ее предыдущие значения. Потом алгоритм, подставляя внутренние параметры, сам избирает наиболее пригодную модель прогнозирования. Существует целая иерархия моделей Бокса-Дженкинса. Логично ее можно определить так:
AR(p)+MA(q) → ARMA(p,q) → ARMA(p,q)(P,Q) → ARIMA(p,q,r)(P,Q,R) →...
Методология прогнозирования Бокса-Дженкинса отличается от большинства методов, потому что в ней не допускается какой-либо особенной структуры данных часовых рядов, для которых выполняется прогноз. В ней используется итеративный подход к определению допустимой модели среди общего класса моделей. Потом выбранная модель сопоставляется с историческими данными, для того чтобы проверить точно ли она описывает ряды. Модель считается приемлемой, если остатки, в основном, малые, распределенные случайно, и не содержат полезной информации. Если заданная модель не удовлетворительна, процесс повторяется, но уже с использованием новой улучшившей модели. Подобная итерационная процедура повторяется до тех пор, пока не будет найденной удовлетворительной модели. Из этого момента заданная модель может использоваться для целей прогнозирования. На рисунке иллюстрируется стратегия выбора модели согласно метода Бокса-Дженкинса.
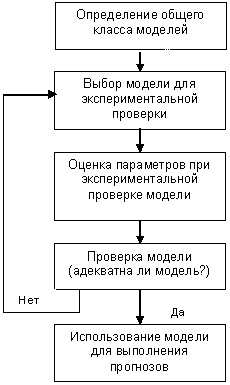 Рис.2 - Блок-схема стратегии выбора модели согласно методу Бокса-Дженкинса Рис.2 - Блок-схема стратегии выбора модели согласно методу Бокса-Дженкинса
| | | | Модель ARIMA
|
Внутренняя структура динамического ряда, зависимость уровня yt от предыдущих его значений yt-1, yt-2,..., yt-p описываетсяавторегрессионной функцией:
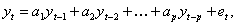 где р – порядок авторегрессии;
ap – коэффициент авторегрессии.
Процесс авторегрессии порядка р функционально связан с автокорреляционной функцией
где р – порядок авторегрессии;
ap – коэффициент авторегрессии.
Процесс авторегрессии порядка р функционально связан с автокорреляционной функцией
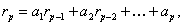 где p = 1,2,...m – лаг автокорреляции (сдвигание yt на p значений назад);
r0 = 1 Согласно с этим соотношением единственный коэффициент авторегрессии первого порядка
где p = 1,2,...m – лаг автокорреляции (сдвигание yt на p значений назад);
r0 = 1 Согласно с этим соотношением единственный коэффициент авторегрессии первого порядка 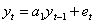 равняется коэффициенту автокорреляции первого порядка, то есть a1 = r1. Для авторегрессии второго порядка равняется коэффициенту автокорреляции первого порядка, то есть a1 = r1. Для авторегрессии второго порядка 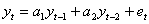 имеем систему уравнений имеем систему уравнений
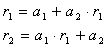 Отсюда
Отсюда 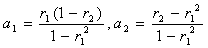 .
Следовательно, коэффициент авторегрессии, как и коэффициент автокорреляции, изменяются в границах от –1 до +1.
При моделировании нестационарных по своей природе экономических процессов, авторегрессионная функция объединяется с другими методами анализа динамики: скользящей средней, трендом, сезонной волной. Объединение разных моделей в единственное целое существенно расширяет сферу их использования. Кроме того, Объединенные модели формируются на основе одних и тех же статистических характеристик – автокорреляционных функций, разрабатывается один алгоритм расчета параметров модели и определения прогнозов.
В модели ARIMA уровень динамического ряда yt определяется как взвешенная сумма предыдущих его значений и значений остатков et – текущих и предыдущих. Она объединяет модель авторегрессии порядка р и модель скользящей средней остатков порядка q. Тренд включается в ARIMA с помощью оператора конечных разностей ряда yt. Для фильтрации линейного тренда используют разницы первого порядка, для фильтрации параболического тренда – разницы второго порядка и т.д. Разница d должна быть стационарной.
Вид модели ARIMA, адекватность ее реальному процессу и прогнозные свойства зависят от порядка авторегрессии р и порядка скользящей средней q. Через то ключевым моментом моделирования считается процедура идентификации – обоснования вида модели. В стандартной методике ARIMA идентификация сводится к визуальному анализу автокоррелограмм и основывается на принципе экономии, по которому (p + q) <= 2.
Модель ARIMA порядка (р,d,q) достаточно гибкая и описывает широкий спектр несезонных процессов. При наличии сезонных колебаний в модели учитывается их периодичность с лагом s (для квартальных данных s = 4, для помесячных s = 12), и аналогичного смысла параметрами (P,D,Q)s. Порядок мультипликативной модели ARIMA составляет .
Следовательно, коэффициент авторегрессии, как и коэффициент автокорреляции, изменяются в границах от –1 до +1.
При моделировании нестационарных по своей природе экономических процессов, авторегрессионная функция объединяется с другими методами анализа динамики: скользящей средней, трендом, сезонной волной. Объединение разных моделей в единственное целое существенно расширяет сферу их использования. Кроме того, Объединенные модели формируются на основе одних и тех же статистических характеристик – автокорреляционных функций, разрабатывается один алгоритм расчета параметров модели и определения прогнозов.
В модели ARIMA уровень динамического ряда yt определяется как взвешенная сумма предыдущих его значений и значений остатков et – текущих и предыдущих. Она объединяет модель авторегрессии порядка р и модель скользящей средней остатков порядка q. Тренд включается в ARIMA с помощью оператора конечных разностей ряда yt. Для фильтрации линейного тренда используют разницы первого порядка, для фильтрации параболического тренда – разницы второго порядка и т.д. Разница d должна быть стационарной.
Вид модели ARIMA, адекватность ее реальному процессу и прогнозные свойства зависят от порядка авторегрессии р и порядка скользящей средней q. Через то ключевым моментом моделирования считается процедура идентификации – обоснования вида модели. В стандартной методике ARIMA идентификация сводится к визуальному анализу автокоррелограмм и основывается на принципе экономии, по которому (p + q) <= 2.
Модель ARIMA порядка (р,d,q) достаточно гибкая и описывает широкий спектр несезонных процессов. При наличии сезонных колебаний в модели учитывается их периодичность с лагом s (для квартальных данных s = 4, для помесячных s = 12), и аналогичного смысла параметрами (P,D,Q)s. Порядок мультипликативной модели ARIMA составляет 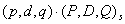 .
Самые простые виды моделей ARIMA: .
Самые простые виды моделей ARIMA:
- (1,0,0) – авторегрессионная функция;
- (0,1,0) – скользящая средняя;
- (1,0,1) – комбинированная модель авторегрессии и скользящей средней;
- (0,1,1) – экспоненциальная средняя;
- (1,1,1) – нестационарный процесс с линейным трендом;
- (0,1,1)×(0,1,1) – мультипликативная модель сезонного процесса.
Сезонные данные имеют четкую структуру, которая повторяется каждый год. В месячных данных с годовой сезонной структурой значения для тех же месяцев в разные годы должны коррелировать между собой, т.е коррелировать между собой должны не только отдельные наблюдения в течение одного и того же года, но и наблюдения с периодом, кратным целому году. Коэффициенты автокорреляции и частичной автокорреляции подобных данных будут ненулевыми при небольших интервалах опоздания (внутренние взаимосвязи). Интерпретация коэффициентов автокорреляции и частичной автокорреляции при сезонных интервалах будет такой же, как и для коэффициентов автокорреляции и частичной автокорреляции при малых интервалах.
Сезонные модели ARIMA включают в себя обычные авторегрессионные члены и члены скользящего среднего, которые отвечают за корреляции при низких интервалах, а также авторегрессионные члены и члены скользящего среднего, которые отвечают за автокорреляции и частичные автокорреляции при сезонных интервалах. В случае нестационарных сезонных рядов для достижения полноты описания часто необходимо дополнительно учесть в модели сезонные разницы.
| | |  Критерии выбора модели Критерии выбора модели
|
Модели ARIMA устанавливаются (выбираются) путем анализа исследуемого ряда и сравнения структуры его функций выборочной автокорреляции и частичной автокорреляции с известной теоретической структурой процессов ARIMA. Однако этой процедуре присуща определенная доля субъективизма и возможно, что две (или более) моделей будут достаточно точно отвечать имеющейся структуре функций выборочной автокорреляции и частичной автокорреляции. Более того, после оценки и проверки может оказаться, что обе модели вполне адекватно описывают данные. Если модели содержат одинаковое количество параметров, тогда преимущество следует отдать модели с наименьшей среднеквадратичной ошибкой s2. Если количество параметров в моделях разное, то по принципу экономии рекомендуется более простая модель. Однако модели с большим количеством параметров могут иметь существенно меньшую среднеквадратичную ошибку.
Учитывая все вышесказанное, было разработано несколько подходов к выбору модели, которые учитывают как качества модели, так и количество ее параметров. Информационный критерий Akaike или AIC [2], позволяет выбрать наилучшую модель из группы моделей-претендентов. Согласно этому критерию, выбирается модель, которая минимизирует выражение
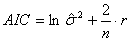 ,
где ,
где 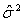 – остаточная сумма квадратов, деленная на количество наблюдений; n – количество наблюдений; r – общее количество слагаемых (включительно с постоянным слагаемым) в модели ARIMA.
Согласно с Байесовским информационным критерием или ВIС [2], выбирается та модель, которая минимизирует следующее выражение – остаточная сумма квадратов, деленная на количество наблюдений; n – количество наблюдений; r – общее количество слагаемых (включительно с постоянным слагаемым) в модели ARIMA.
Согласно с Байесовским информационным критерием или ВIС [2], выбирается та модель, которая минимизирует следующее выражение
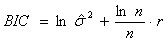 Второе слагаемое в формулах АІС и ВIС – это "штрафной фактор", который учитывает привлечение к модели дополнительных параметров. Критерий ВIС налагает более ограничений на количество параметров сравнительно с критерием АІС. Потому минимизация критерия ВIС при выборе модели всегда дает количество параметров, не превышающее количество, установленное согласно с критерием АІС. Часто оба критерия дают одинаковый результат. Критерии АІС и ВIС следует рассматривать как дополнительные процедуры, призванные помочь при окончательном выборе модели. Они не в состоянии полностью заменить внимательное изучение поведения выборочных коэффициентов автокорреляции и частичной автокорреляции.
В работе модель, позволяющая осуществить наиболее качественный прогноз, определяется с помощью двух критериев. Критериями выбора лучшей модели являются следующие: максимизация значения вероятности осуществления правильного (адекватного) прогноза, которое вычисляется для каждой из моделей ARIMA с различным набором параметров отдельно для осуществляемого прогноза с разными значениями временного окна (m1 = 15 и m2= 30), и минимизация средней квадратичной ошибки.
Значение вероятности рассчитывается следующим образом:
Второе слагаемое в формулах АІС и ВIС – это "штрафной фактор", который учитывает привлечение к модели дополнительных параметров. Критерий ВIС налагает более ограничений на количество параметров сравнительно с критерием АІС. Потому минимизация критерия ВIС при выборе модели всегда дает количество параметров, не превышающее количество, установленное согласно с критерием АІС. Часто оба критерия дают одинаковый результат. Критерии АІС и ВIС следует рассматривать как дополнительные процедуры, призванные помочь при окончательном выборе модели. Они не в состоянии полностью заменить внимательное изучение поведения выборочных коэффициентов автокорреляции и частичной автокорреляции.
В работе модель, позволяющая осуществить наиболее качественный прогноз, определяется с помощью двух критериев. Критериями выбора лучшей модели являются следующие: максимизация значения вероятности осуществления правильного (адекватного) прогноза, которое вычисляется для каждой из моделей ARIMA с различным набором параметров отдельно для осуществляемого прогноза с разными значениями временного окна (m1 = 15 и m2= 30), и минимизация средней квадратичной ошибки.
Значение вероятности рассчитывается следующим образом:
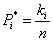 ,
где ki – количество случаев, когда полученное прогнозное значение отклоняется от реального не более чем на ± 2 σ, n – общее число прогнозных значений.
После вычисления всех значений ,
где ki – количество случаев, когда полученное прогнозное значение отклоняется от реального не более чем на ± 2 σ, n – общее число прогнозных значений.
После вычисления всех значений 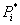 , находится максимальное из них ( , находится максимальное из них (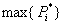 ) и именно модель с iым набором параметров признается лучшей по данному критерию. В ходе работы для осуществления краткосрочного прогноза по имеющимся данным колебания валютных курсов, применяется модель ARIMA (p,d,q) для различных значений временного окна и прогнозирование осуществляется на следующий бар (на одно значение вперед), и полученные результаты сравниваются между собой.
Вторым критерием выбора наиболее подходящей модели является минимизация средней квадратичной ошибки прогноза, полученного с помощью определенной модели. Значение ошибки вычисляется следующим образом: ) и именно модель с iым набором параметров признается лучшей по данному критерию. В ходе работы для осуществления краткосрочного прогноза по имеющимся данным колебания валютных курсов, применяется модель ARIMA (p,d,q) для различных значений временного окна и прогнозирование осуществляется на следующий бар (на одно значение вперед), и полученные результаты сравниваются между собой.
Вторым критерием выбора наиболее подходящей модели является минимизация средней квадратичной ошибки прогноза, полученного с помощью определенной модели. Значение ошибки вычисляется следующим образом:
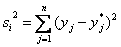 ,
где yj – реальные данные ,
где yj – реальные данные 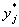 – данные, полученные в результате прогнозирования с помощью iой модели.
После вычисления всех значений – данные, полученные в результате прогнозирования с помощью iой модели.
После вычисления всех значений 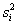 , находится минимальное из них ( , находится минимальное из них (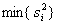 ) и именно модель с iым набором параметров признается лучшей согласно данному критерию. ) и именно модель с iым набором параметров признается лучшей согласно данному критерию.
| | |  Выводы Выводы
|
Прогнозирование с большим значением временного окна дает более точный результат, т.к. прогнозирование с помощью моделей ARIMA выполняется путем анализа информации, которая содержится в предыстории временного ряда, а чем больше временное окно, тем большее количество информации имеется для выполнения анализа и построения качественного прогноза.
Достоинства моделей ARIMA:
- Подход Бокса-Дженкинса к анализу временных рядов является весьма мощным инструментом для построения точных прогнозов с малой дальностью прогнозирования.
- Модели ARIMA достаточно гибкие и могут описывать широкий спектр характеристик временных рядов, которые встречаются на практике.
Однако использование моделей ARIMA имеет и несколько недостатков:
- Необходимо относительно большое количество исходных данных
- Не существует простого способа корректировки параметров моделей ARIMA, – когда привлекаются новые данные, модель приходится почти полностью перестраивать, а иногда требуется выбор абсолютно новой модели.
- Также для оценок используется та или иная модель, а это означает наличие модельного риска в расчетах. Поэтому необходима периодическая проверка адекватности применяемой модели.
- Таким образом, общий недостаток прогнозирования при помощи этих моделей заключается в том, что все они независимо от применяемых методов вычисления используют исторические данные. И если условия на рынке (например, волатильность рынка или корреляция между активами) резко меняются, то эти изменения будут учтены только через определенный промежуток времени. А до этого момента предсказания будут некорректны.
Вышеназванные факторы приводят к тому, что данные модели хорошо работают в случае стабильного состояния рынков и перестают адекватно отражать поведение цен, когда на рынках происходят существенные изменения.
В результате работы будет сделан вывод о правилах применения модели ARIMA с различными наборами параметров для осуществления краткосрочного прогноза на валютном рынке FOREX и разработаны рекомендации для корректировки трейдерами стратегии своего поведения и эффективного управления своими активами.
Примечание: В настоящий момент работа находится в стадии разработки, исследования в полном объеме еще не закончены, завершение планируется в декабре 2007г.
В работе планируется дополнительно провести анализ прогнозирования ценовых графиков с разным значением временного окна с помощью следующих моделей:
- (1,0,0) – авторегрессионная функция;
- (0,0,1) – скользящая средняя;
- (1,0,1) – комбинированная модель авторегрессии и скользящей средней;
- (0,1,1) – экспоненциальная средняя;
- (1,1,1) – нестационарный процесс с линейным трендом
| | |  Перечень ссылок Перечень ссылок
| |
1. Єріна А. М. "Статистичнемоделювання та прогнозування", Навчальнийпосібник. – К.: КНЕУ, 2001. – 170с.
2. Ханк Дж., Райтс А. "Бизнес-прогнозирование", 7-е издание: Пер. с английского. – М.:"Вильямс", 2003. – 656с.
3. Басовский Л. Е. "Прогнозирование и планирование в условиях рынка", Учебное пособие - М.: ИНФРА-М, 2001. - 260с.
4. Бокс Дж., Дженкинс Г. "Анализ временных рядов. Прогноз и управление" – М.: Мир, 1994 г.
5. Кендэлл М. "Временные ряды" Москва, Финансы и статистика, 1981 г.
| |
 Рис.2 - Блок-схема стратегии выбора модели согласно методу Бокса-Дженкинса
Рис.2 - Блок-схема стратегии выбора модели согласно методу Бокса-Дженкинса
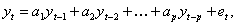 где р – порядок авторегрессии;
ap – коэффициент авторегрессии.
Процесс авторегрессии порядка р функционально связан с автокорреляционной функцией
где р – порядок авторегрессии;
ap – коэффициент авторегрессии.
Процесс авторегрессии порядка р функционально связан с автокорреляционной функцией
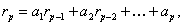 где p = 1,2,...m – лаг автокорреляции (сдвигание yt на p значений назад);
r0 = 1 Согласно с этим соотношением единственный коэффициент авторегрессии первого порядка
где p = 1,2,...m – лаг автокорреляции (сдвигание yt на p значений назад);
r0 = 1 Согласно с этим соотношением единственный коэффициент авторегрессии первого порядка 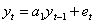 равняется коэффициенту автокорреляции первого порядка, то есть a1 = r1. Для авторегрессии второго порядка
равняется коэффициенту автокорреляции первого порядка, то есть a1 = r1. Для авторегрессии второго порядка 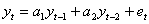 имеем систему уравнений
имеем систему уравнений
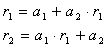 Отсюда
Отсюда 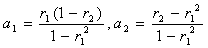 .
Следовательно, коэффициент авторегрессии, как и коэффициент автокорреляции, изменяются в границах от –1 до +1.
При моделировании нестационарных по своей природе экономических процессов, авторегрессионная функция объединяется с другими методами анализа динамики: скользящей средней, трендом, сезонной волной. Объединение разных моделей в единственное целое существенно расширяет сферу их использования. Кроме того, Объединенные модели формируются на основе одних и тех же статистических характеристик – автокорреляционных функций, разрабатывается один алгоритм расчета параметров модели и определения прогнозов.
В модели ARIMA уровень динамического ряда yt определяется как взвешенная сумма предыдущих его значений и значений остатков et – текущих и предыдущих. Она объединяет модель авторегрессии порядка р и модель скользящей средней остатков порядка q. Тренд включается в ARIMA с помощью оператора конечных разностей ряда yt. Для фильтрации линейного тренда используют разницы первого порядка, для фильтрации параболического тренда – разницы второго порядка и т.д. Разница d должна быть стационарной.
Вид модели ARIMA, адекватность ее реальному процессу и прогнозные свойства зависят от порядка авторегрессии р и порядка скользящей средней q. Через то ключевым моментом моделирования считается процедура идентификации – обоснования вида модели. В стандартной методике ARIMA идентификация сводится к визуальному анализу автокоррелограмм и основывается на принципе экономии, по которому (p + q) <= 2.
Модель ARIMA порядка (р,d,q) достаточно гибкая и описывает широкий спектр несезонных процессов. При наличии сезонных колебаний в модели учитывается их периодичность с лагом s (для квартальных данных s = 4, для помесячных s = 12), и аналогичного смысла параметрами (P,D,Q)s. Порядок мультипликативной модели ARIMA составляет
.
Следовательно, коэффициент авторегрессии, как и коэффициент автокорреляции, изменяются в границах от –1 до +1.
При моделировании нестационарных по своей природе экономических процессов, авторегрессионная функция объединяется с другими методами анализа динамики: скользящей средней, трендом, сезонной волной. Объединение разных моделей в единственное целое существенно расширяет сферу их использования. Кроме того, Объединенные модели формируются на основе одних и тех же статистических характеристик – автокорреляционных функций, разрабатывается один алгоритм расчета параметров модели и определения прогнозов.
В модели ARIMA уровень динамического ряда yt определяется как взвешенная сумма предыдущих его значений и значений остатков et – текущих и предыдущих. Она объединяет модель авторегрессии порядка р и модель скользящей средней остатков порядка q. Тренд включается в ARIMA с помощью оператора конечных разностей ряда yt. Для фильтрации линейного тренда используют разницы первого порядка, для фильтрации параболического тренда – разницы второго порядка и т.д. Разница d должна быть стационарной.
Вид модели ARIMA, адекватность ее реальному процессу и прогнозные свойства зависят от порядка авторегрессии р и порядка скользящей средней q. Через то ключевым моментом моделирования считается процедура идентификации – обоснования вида модели. В стандартной методике ARIMA идентификация сводится к визуальному анализу автокоррелограмм и основывается на принципе экономии, по которому (p + q) <= 2.
Модель ARIMA порядка (р,d,q) достаточно гибкая и описывает широкий спектр несезонных процессов. При наличии сезонных колебаний в модели учитывается их периодичность с лагом s (для квартальных данных s = 4, для помесячных s = 12), и аналогичного смысла параметрами (P,D,Q)s. Порядок мультипликативной модели ARIMA составляет 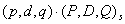 .
Самые простые виды моделей ARIMA:
.
Самые простые виды моделей ARIMA:
 Критерии выбора модели
Критерии выбора модели
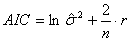 ,
где
,
где 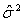 – остаточная сумма квадратов, деленная на количество наблюдений; n – количество наблюдений; r – общее количество слагаемых (включительно с постоянным слагаемым) в модели ARIMA.
Согласно с Байесовским информационным критерием или ВIС [2], выбирается та модель, которая минимизирует следующее выражение
– остаточная сумма квадратов, деленная на количество наблюдений; n – количество наблюдений; r – общее количество слагаемых (включительно с постоянным слагаемым) в модели ARIMA.
Согласно с Байесовским информационным критерием или ВIС [2], выбирается та модель, которая минимизирует следующее выражение
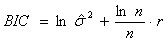 Второе слагаемое в формулах АІС и ВIС – это "штрафной фактор", который учитывает привлечение к модели дополнительных параметров. Критерий ВIС налагает более ограничений на количество параметров сравнительно с критерием АІС. Потому минимизация критерия ВIС при выборе модели всегда дает количество параметров, не превышающее количество, установленное согласно с критерием АІС. Часто оба критерия дают одинаковый результат. Критерии АІС и ВIС следует рассматривать как дополнительные процедуры, призванные помочь при окончательном выборе модели. Они не в состоянии полностью заменить внимательное изучение поведения выборочных коэффициентов автокорреляции и частичной автокорреляции.
В работе модель, позволяющая осуществить наиболее качественный прогноз, определяется с помощью двух критериев. Критериями выбора лучшей модели являются следующие: максимизация значения вероятности осуществления правильного (адекватного) прогноза, которое вычисляется для каждой из моделей ARIMA с различным набором параметров отдельно для осуществляемого прогноза с разными значениями временного окна (m1 = 15 и m2= 30), и минимизация средней квадратичной ошибки.
Значение вероятности рассчитывается следующим образом:
Второе слагаемое в формулах АІС и ВIС – это "штрафной фактор", который учитывает привлечение к модели дополнительных параметров. Критерий ВIС налагает более ограничений на количество параметров сравнительно с критерием АІС. Потому минимизация критерия ВIС при выборе модели всегда дает количество параметров, не превышающее количество, установленное согласно с критерием АІС. Часто оба критерия дают одинаковый результат. Критерии АІС и ВIС следует рассматривать как дополнительные процедуры, призванные помочь при окончательном выборе модели. Они не в состоянии полностью заменить внимательное изучение поведения выборочных коэффициентов автокорреляции и частичной автокорреляции.
В работе модель, позволяющая осуществить наиболее качественный прогноз, определяется с помощью двух критериев. Критериями выбора лучшей модели являются следующие: максимизация значения вероятности осуществления правильного (адекватного) прогноза, которое вычисляется для каждой из моделей ARIMA с различным набором параметров отдельно для осуществляемого прогноза с разными значениями временного окна (m1 = 15 и m2= 30), и минимизация средней квадратичной ошибки.
Значение вероятности рассчитывается следующим образом:
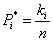 ,
где ki – количество случаев, когда полученное прогнозное значение отклоняется от реального не более чем на ± 2 σ, n – общее число прогнозных значений.
После вычисления всех значений
,
где ki – количество случаев, когда полученное прогнозное значение отклоняется от реального не более чем на ± 2 σ, n – общее число прогнозных значений.
После вычисления всех значений 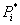 , находится максимальное из них (
, находится максимальное из них (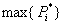 ) и именно модель с iым набором параметров признается лучшей по данному критерию. В ходе работы для осуществления краткосрочного прогноза по имеющимся данным колебания валютных курсов, применяется модель ARIMA (p,d,q) для различных значений временного окна и прогнозирование осуществляется на следующий бар (на одно значение вперед), и полученные результаты сравниваются между собой.
Вторым критерием выбора наиболее подходящей модели является минимизация средней квадратичной ошибки прогноза, полученного с помощью определенной модели. Значение ошибки вычисляется следующим образом:
) и именно модель с iым набором параметров признается лучшей по данному критерию. В ходе работы для осуществления краткосрочного прогноза по имеющимся данным колебания валютных курсов, применяется модель ARIMA (p,d,q) для различных значений временного окна и прогнозирование осуществляется на следующий бар (на одно значение вперед), и полученные результаты сравниваются между собой.
Вторым критерием выбора наиболее подходящей модели является минимизация средней квадратичной ошибки прогноза, полученного с помощью определенной модели. Значение ошибки вычисляется следующим образом:
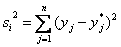 ,
где yj – реальные данные
,
где yj – реальные данные 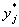 – данные, полученные в результате прогнозирования с помощью iой модели.
После вычисления всех значений
– данные, полученные в результате прогнозирования с помощью iой модели.
После вычисления всех значений 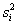 , находится минимальное из них (
, находится минимальное из них (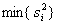 ) и именно модель с iым набором параметров признается лучшей согласно данному критерию.
) и именно модель с iым набором параметров признается лучшей согласно данному критерию.