Уравнение движения груза, подвешенного на пружине.
Рассмотрим грузик массой m подвешенный на пружине жесткости k.
В положении равновесия пружина растянута на величину 
.
Оттянем шарик в вертикальном направлении на расстояние x и запишем уравнение движения шарика:
Подставив в уравнение значение 
получим:
Обратим внимание на то, что уравнение движения не зависит от силы тяжести, действующей на тело. Это связано с тем, что сила тяжести – консервативная сила.
Разделим обе части уравнения на массу груза и введем новую переменную 
, получим:
Это уравнение называется уравнением колебаний груза. Физический смысл уравнения прост: ускорение груза прямо пропорционально его координате (в системе отсчета связанной с положением равновесия), взятой с противоположным знаком.
Величина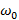 
– это циклическая частота колебаний, но о ней мы поговорим позже.
Уравнение движения математического маятника.
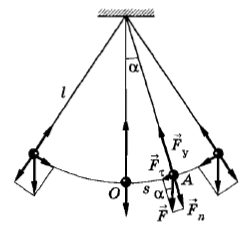Рассмотрим груз, подвешенный на длинной нерастяжимой нити.
Рассмотрим систему координат, движущуюся вместе с грузом, одна ось которой направлена вдоль нити (назовем ее нормальной), другая, перпендикулярна первой, направлена по касательной к дуге окружности, вдоль которой происходит движение (она всегда будет направлена вдоль вектора скорости груза, назовем ее тангенциальной).
В такой системе координат сила тяжести, действующая на груз раскладывается на нормальную и тангенциальную компоненты. Нормальная компонента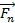 
будет компенсироваться силой натяжения нити, в то время как тангенциальная 
будет вызывать колебания.
При отклонении маятника на угол α от вертикали 
.
Тогда уравнение движения груза вдоль оси, сонаправленной со скоростью запишется следующим образом:
|
|
Если длина нити l, а s – это длина дуги окружности от положения равновесия до местоположения тела, то 
. Сократив массу груза и учтя, что при малых значениях α справедлив замечательный предел 
, получим:
Как видно, уравнение движения двух различных систем имеют совершенно аналогичный вид. На самом деле подобным уравнением можно описать любой незатухающий колебательный процесс.
Гармонические колебания.
Немного физико-математической сложности:
Ускорение это вторая производная координаты тела по времени. Из математики мы знаем периодические функции, вторая производная которых является той же функцией, но с противоположным знаком – это функции синуса и косинуса. Если точно, то:
.
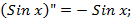
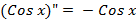Но нашему уравнению 
это пока не удовлетворяет. Чтобы в выражении появился коэффициент 
и выражение менялось не в пределах ±1, нужно рассмотреть
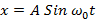
Тогда вторая производная этого чуда будет равна:
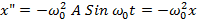
что нам и требовалось. В математике так же доказывается, что функции синуса и косинуса единственны в своем роде и других функций отвечающих вышеописанным требованиям нет.
Общим же решением нашего уравнения будет:
где величина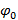 
определяется не самим уравнением, а начальными условиями задачи.
Небольшой подытог:
Периодические изменения физической величины в зависимости от времени по закону синуса или косинуса называются гармоническими колебаниями.
Амплитудой А гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия.