Для описания поступательного движения тела применим теорему о движении центра масс механической системы: центр масс движется так же, как двигалась бы материальная точка, обладающая массой механической системы при действии на нее главного вектора внешних сил, т.е.
; (3.а)
Записав проекции выражения (3.а) на неподвижные оси плоской декартовой координатной системы получим:
. (3.б)
Для описания вращения тела вокруг неподвижной оси необходимо записать дифференциальное уравнение первого порядка относительно угловой скорости вращения либо дифференциальное уравнением второго порядка относительно угла поворота тела:
или 
, (4)
где 
и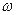 
- угловое ускорение и угловая скорость вращения, 
- момент инерции тела относительно оси вращения, 
- проекция главного момента внешних сил на ось вращения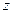 
.
Для осуществления плоского движения свободного твердого тела необходимо выполнение следующих условий: масса тела должна быть распределена симметрично относительно плоскости движения, проходящей через центр масс; начальные скорости точек тела должны быть расположены в плоскостях, параллельных плоскости движения; главный вектор внешних сил должен лежать в этой плоскости, а главный момент - быть перпендикулярным к ней.
Для несвободного тела движение может быть плоским и в силу наложенных на него связей.
В задачах динамики в качестве полюса удобно выбирать центр масс тела С – в этом случае дифференциальные уравнения движения будут иметь наиболее простой вид:
.
; (5)
.
Более подробно с материалом можно познакомиться, например, в [1], [5], [7].
Если к дифференциальным уравнениям движения тел добавить уравнения кинематических связей, можно получить математическую модель для исследования движения тел механической системы. Очевидно, что полученная система уравнений должна быть замкнута (число уравнений должно совпадать с числом неизвестных); для выполнения расчета параметров движения следует учесть начальные (или краевые) условия.
|
|
ПРИМЕР 1. Для механической системы, изображенной на рис.1, и состоящей из груза 1, прикрепленного к земле пружиной, двух соосных (насаженных неподвижно на единую ось) блоков и однородного диска, составить замкнутую систему дифференциальных и алгебраических уравнений. Жесткость пружины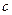 
, вес груза 
, вес соосных блоков 
, их радиусы 
и 
, а так же осевой момент инерции 
, вес однородного диска 
и его радиус 
, коэффициент трения качения 
известны.
РЕШЕНИЕ. Мысленно расчленим механическую систему на три тела (груз, соосные блоки и диск), приложив к каждому из тел соответствующие внешние силы (см.рис.1).
Запишем дифференциальное уравнение движения для первого груза: 
.
Полагая, что в начальном положении механической системы пружина не деформирована, выражение для силы упругости будет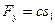 
.
Дифференциальное уравнение вращения для соосных блоков будет: 
.
Поскольку центр соосных блоков неподвижен, суммы проекций действующих сил на горизонтальную и вертикальную оси будут:
; 
.
Теперь запишем дифференциальные уравнения движения диска в предположении 
: 
; 
; здесь 
.
Как уже говорилось выше, момент трения качения при смене знака скорости (при 
) изменит направление.
С учетом этого замечания дифференциальное уравнение вращения вокруг центра масс диска примет вид
|
|
, где 
- знак скорости по координате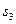 
.
Заметим, что такой особенностью обладает только это уравнение движения.
Поскольку центр масс диска движется вдоль наклонной плоскости, сумма проекций действующих сил на нормаль к этой плоскости должна равняться нулю:
.
Теперь запишем уравнения кинематических связей:
или 
;
или 
;
или 
При их записи учтено, что скорости точек на нерастяжимой нити одинаковы, а мгновенный центр диска расположен в точке соприкосновения с наклонной плоскостью.
Рассмотренная механическая система обладает одной степенью свободы, т.е. из четырех введенных координат независимой является только одна.
Дифференцирование уравнений кинематических связей позволяет записать аналогичные соотношения для ускорений, а интегрирование – для перемещений.
В итоге получена замкнутая система из двенадцати уравнений с двенадцатью неизвестными.
Замечание: рассмотренный подход является универсальным, так как позволяет решать задачи о движении механических систем, состоящих из любого числа тел и обладающих любым числом степеней свободы. 