Т а б л и ц а 2.3 – Третья группа предприятий

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Петербургский государственный университет путей сообщения

Императора Александра I»

(ФГБОУ ВО ПГУПС)

 

Факультет «Экономика и менеджмент»

Кафедра «Экономика транспорта»

 

Специальность 23.05.04 Эксплуатация железных дорог

Специализация Магистральный транспорт

 

ТИПОВАЯ ЗАДАЧА

по дисциплине «Статистика»

на тему: «Показатели вариации»

 

 

Вариант: 8

 

Обучающийся Курс 2 Группа УПП-706 форма обучения – очная 05-706-08 номер зачетной книжки	__________________ подпись, дата	А.А.Кибкало
Руководитель	__________________ подпись, дата	доц, В.М.Артимович

 

Санкт-Петербург

 

 

Содержание

 

1.Исходные статистические данные. 3

2. Решение. 3

2.1 Группы предприятий. 3

2.2 Задача. 7

Вывод. 8

 

 

1.Исходные статистические данные.

Данные взяты их Темы 1.

Рассчитать и представить в таблице по каждой группе показатели: размах вариации, среднее линейное отклонение, внутригрупповую дисперсию, среднее квадратическое отклонение, коэффициент вариации и общую дисперсию по всей совокупности;

В соответствии с вариантом решить задачу:

Задача 8. Распределение основных фондов по предприятиям отрасли характеризуется следующими данными:

 

Таблица 1 – Основные фонды предприятий

 

Группы предприятий по стоимости основных фондов, тыс. руб.	Число предприятий	Основные фонды в среднем на предприятии, тыс. руб.	Групповые дисперсии
12–27			1,14
27–42			1,09
42–57			1,69
57–72			1,84

 

Определить:

а) среднюю из групповых дисперсий;

б) межгрупповую дисперсию;

в) общую дисперсию.

Решение

Группы предприятий

Т а б л и ц а 2. 1 – Первая группа предприятий

Код предприятия	Основные производственные фонды, млн.руб.	Xi-Xср	(Xi-Xср)2
	1,1	1,01	1,02
	1,2	0,91	0,83
	1,2	0,91	0,83
	1,3	0,81	0,65
	1,4	0,71	0,50
	1,4	0,71	0,50
	1,4	0,71	0,50
	1,4	0,71	0,50
	1,6	0,51	0,26
	1,7	0,41	0,17
	1,8	0,31	0,10
	1,8	0,31	0,10
	1,9	0,21	0,04
	2,2	0,09	0,01
	2,3	0,19	0,04
	2,4	0,29	0,08
	2,5	0,39	0,15
	2,8	0,69	0,48
	2,8	0,69	0,48
	2,8	0,69	0,48
	2,9	0,79	0,63
	4,2	2,09	4,37
	4,4	2,29	5,25
Итого		16,43	17,96

Размах вариации представляет собой разность между максимальным и минимальным значением признака исследуемой совокупности:

R=x_max-x_min=4.4-1.1=3.3 млн.руб

Среднее арифметическое стоимости основных фондов: X_cp=2.11

Среднее линейное отклонение – это средняя арифметическая абсолютных отклонений значений признака от среднего уровня:

Дисперсия – это средняя из квадратов отклонений от средней арифметической:

Среднее квадратическое отклонение – показатель вариации, характеризующий величину, на которую в среднем признаки по единица наблюдения отличаются от средней арифметической:

Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:

Т а б л и ц а 2.2– Вторая группа предприятий

Код предприятия	Основные производственные фонды, млн.руб.	Xi-Xср	(Xi-Xср)2
	4,8	0,84	0,71
	4,8	0,84	0,71
		0,64	0,41
		0,64	0,41
	5,1	0,54	0,29
	5,5	0,14	0,02
	5,5	0,14	0,02
	5,5	0,14	0,02
	5,8	0,16	0,03
	6,4	0,76	0,58
	6,8	1,16	1,34
	7,5	1,86	3,45
Итого		7,87	7,99

 

Размах вариации: R=x_max-x_min=7,5-4,8=2,7 млн.руб

Среднее арифметическое стоимости основных фондов: X_cp=5,64

Среднее линейное отклонение:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент вариации:

Т а б л и ц а 2.3 – Третья группа предприятий

Код предприятия	Основные производственные фонды, млн.руб.	Xi-Xср	(Xi-Xср)2
	8,2	0,80	0,64
	9,1	0,10	0,01
	9,7	0,70	0,49
Итого		1,60	1,14

Размах вариации: R=x_max-x_min=9,7-8,2=1,5 млн.руб

Среднее арифметическое стоимости основных фондов: X_cp=9,0

Среднее линейное отклонение:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент вариации: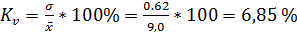

Таблица 2.4 – Четвертая группа предприятий

Код предприятия	Основные производственные фонды, млн.руб.	Xi-Xср	(Xi-Xср)2
	17,4	0,35	0,12
	18,1	0,35	0,12
Итого		0,70	0,25

 

Размах вариации: R=x_max-x_min=18,1-17,4=0,7 млн.руб

Среднее арифметическое стоимости основных фондов: X_cp=17,75

Среднее линейное отклонение:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент вариации:

Таблица 2.5 - Степенные и позиционные средние величины по группам.

№	Группа предприятий по cтоимости основных фондов, тыс. руб.	Число предприятий в группе	R	Xср	dпр	δ	δ2	Kv
	1,1-4,5		3,3	2,11	0,71	0,78	0,88	41,7
	4,5-7,9		2,7	5,64	0,66	0,67	0,82	14,46
	7,9-11,3		1,5		0,53	0,38	0,62	6,85
	14,7-18,1		0,7	17,75	0,35	0,12	0,35	1,9

 

Задача

Таблица 2.6 – Основные фонды предприятий и сумма всех фондов

Группы предприятий по стоимости основных фондов, тыс.руб.	Число предприятий	Основные фонды в среднем на предприятии, тыс.руб.	Групповые дисперсии	Сумма фондов	()2
12–27			1,14		413,44
27–42			1,09		40,11
42–57			1,69		93,44
57–72			1,84		940,44
Итого

 

Общую среднюю ищем, поделив сумму фондов на общее число предприятий:

Средняя из внутригрупповых дисперсий:

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она рассчитывается по формуле:

Где – средняя по i- ой группе; m_i – численность по i- ой группе, x₀ - общая средняя для всей изучаемой совокупности

Общая дисперсия равна сумме из средней внутригрупповой и межгрупповой дисперсий:

Вывод

 

Таким образом, степенные и позиционные средние величины по группам предприятий, сгруппированных по стоимости основных фондов, указаны в таблице 2.5.Анализируя данные, можно сделать вывод о том, что первая группа предприятий не является качественно однородной, так как ее коэффициент вариации, равный 41,7 % > 33 %.Остальные группы являются качественно однородными.

Среди предприятий из другой задачи, средняя из внутригрупповых дисперсий составила 1,36. Межгрупповая дисперсия – 237,10. Общая дисперсия – 238, 46.