ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Понятия производной и дифференциала. Дифференцируемость функции
Пусть имеется функция f (x). Возьмем точку  и зададим приращение
и зададим приращение  , т.е.
, т.е. 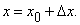 Функция f (x) также получит приращение
Функция f (x) также получит приращение 
Определение. Производной функции f (x) в точке  называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю, т.е.
называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю, т.е. 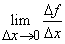 (при условии, что он существует).
(при условии, что он существует).
Обозначают производную штрихом f' (х) (читается «эф штрих от икс») или набором символов  (читается «дэ эф от икс по дэ икс»).
(читается «дэ эф от икс по дэ икс»).
По определению приращений  и
и  в точке
в точке  их отношение
их отношение  представляет собой тангенс угла наклона секущей к оси абсцисс, пересекающей график функции в точках
представляет собой тангенс угла наклона секущей к оси абсцисс, пересекающей график функции в точках  и
и  При
При  секущая будет переходить в касательную в точке
секущая будет переходить в касательную в точке  .
.
Геометрический смысл производной: тангенс угла наклона касательной к оси абсцисс, проведенной к графику функции f (x) в точке  (см. рис.1).
(см. рис.1). 
Рисунок 1
Рассмотрим теперь физический смысл производной. Пусть имеется производная  где х - координата материальной точки, a t - время. Отношение
где х - координата материальной точки, a t - время. Отношение  есть средняя скорость за промежуток времени
есть средняя скорость за промежуток времени  . Производная представляет собой мгновенную скорость материальной точки в момент времени t.
. Производная представляет собой мгновенную скорость материальной точки в момент времени t.
Аналогично,  есть скорость изменения скорости, или ускорение.
есть скорость изменения скорости, или ускорение.
Определение. Функция f (x) называется дифференцируемой в точке  , если ее приращение
, если ее приращение  в этой точке представимо в виде
в этой точке представимо в виде 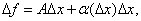 где А - некоторое число, не зависящее от
где А - некоторое число, не зависящее от  , а
, а  - функция аргумента
- функция аргумента  , являющаяся бесконечно малой при
, являющаяся бесконечно малой при  т.е.
т.е. 
Теорема. Для того чтобы функция f (x) была дифференцируема в точке  , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Теорема. Если функция f (х) дифференцируема в точке  , то она и непрерывна в этой точке.
, то она и непрерывна в этой точке.
Замечание. Обратное утверждение не верно. Например,  непрерывна в точке
непрерывна в точке  но не имеет производной в ней.
но не имеет производной в ней.
Запишем приращение дифференцируемой функции  Пусть
Пусть 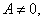 тогда
тогда  - бесконечно малое одного порядка с
- бесконечно малое одного порядка с  , а
, а  - бесконечно малое более высокого порядка, чем
- бесконечно малое более высокого порядка, чем  .
.
Определение. Дифференциалом функции f (х) в точке  называется главная, линейная относительно
называется главная, линейная относительно  часть приращения функции
часть приращения функции  или
или 
Назовем дифференциалом независимой переменной х величину  Получим
Получим  или
или 
Геометрический смысл дифференциала см. на рис.1  .
.
Вычисление производных
Теорема. Если функции u (х) и v (x) дифференцируемы в точке х, то сумма, разность, произведение и частное (в последнем случае  ) этих функций также дифференцируемы в этой точке и имеют место следующие соотношения:
) этих функций также дифференцируемы в этой точке и имеют место следующие соотношения:
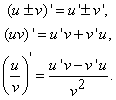
Следствие. Постоянный множитель можно выносить за знак производной.

Теорема (производная сложной функции). Если функция  имеет производную в точке
имеет производную в точке  , a функция y=f (х) имеет производную в соответствующей точке
, a функция y=f (х) имеет производную в соответствующей точке  то функция
то функция  имеет производную в точке
имеет производную в точке  и имеет место следующая формула:
и имеет место следующая формула: 
Пример. 
Примеры:
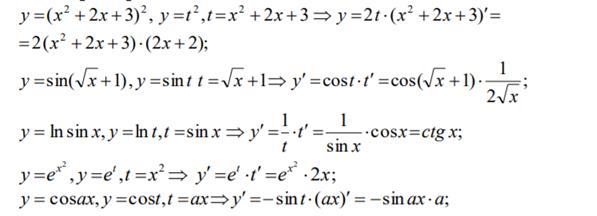
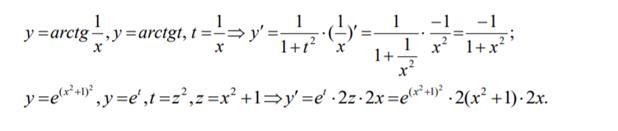
Исследование поведения графиков функций


Пример.  Вычислив производную, найдем
Вычислив производную, найдем  Следовательно, в точке х =0 - локальный минимум.
Следовательно, в точке х =0 - локальный минимум.
Пример.  . Вычислив производную, найдем
. Вычислив производную, найдем  Следовательно, в точке х =0 - локального экстремума нет.
Следовательно, в точке х =0 - локального экстремума нет.
Пример. Найти экстремальные значения функции  (см. рис. 2).
(см. рис. 2).

Рисунок 2
Вычислив производную  и приравняв ее к нулю найдем две точки возможного локального экстремума
и приравняв ее к нулю найдем две точки возможного локального экстремума  =0 и
=0 и  =2.
=2.
Следовательно, точка  =0 - точка локального максимума
=0 - точка локального максимума  а точка
а точка  =2 - точка локального минимума
=2 - точка локального минимума 
