Рефлексивно-оценочная часть.

Конспект урока по теме: «Решение задач»

Глава 3. Многогранники.

§2. Пирамида.

П.33. Правильная пирамида

Учебная задача урока: в совместной деятельности с учащимися закрепить понятие правильной пирамиды и научиться решать задачи на правильную пирамиду.

Диагностируемые цели:

В результате урока ученик:

• Знает

- определение правильной пирамиды

- определение апофемы правильной пирамиды

• Умеет
  - строить правильную пирамиду

- использовать понятия правильной пирамиды и апофемы для решения задач

• Понимает

- что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками
- что площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

Ход урока

1. Мотивационно - ориентировочная часть.

Актуализация

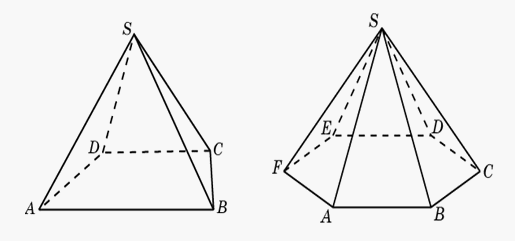
-Какие из представленных пирамид являются правильными? Почему?

1.

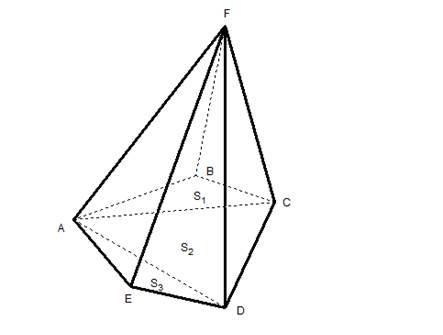
2.

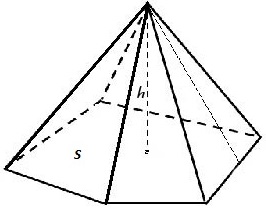
3.

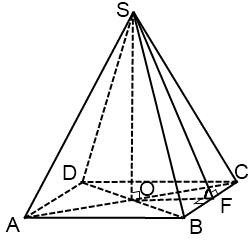
4.

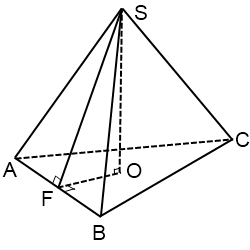
5.
(4,5 т.к. в основании правильные многоугольники и высота падает в центр основания)

-Почему остальные пирамиды не являются правильными?( в основании не правильные многоугольники)

-Сформулируйте определение правильной пирамиды (пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой)

-Что называют апофемой? (высота боковой грани правильной пирамиды, проведенная из ее вершины)

- Чему равна площадь боковой поверхности пирамиды? (площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему)

Тема урока «Решение задач»

2. Операционно-познавательная часть

№ 260

Вопросы:

-Куда упадет высота пирамиды? (на точку пересечения медиан)

-Чем будет являться сечение? (треугольником)
-Если мы мысленно продлим сечение CDO, то что оно пересечет? (грань ADB, получится отрезок DM)

-Давайте определим чем является отрезок DM. Вспомним признак перпендикулярности прямой и плоскости. (прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в плоскости)
-Рассмотрим сначала прямую DO. Какой плоскости она перпендикулярна? (ACB)
-Тогда какой вывод мы можем сделать относительно прямой АВ? ( DO перпендикулярна ACB, следовательно перпендикулярна и AB)
-Вернемся к отрезку DM. Перпендикулярен ли отрезок DM к АВ? Почему? (да, DO перпендикулярна АВ, следовательно вся плоскость CDO перпендикулярна АВ, а прямая DM принадлежит плоскости, значит и она перпендикулярна АВ)

-Чем тогда является прямая DM в грани ADB? (апофемой)
-Переходим к решению. Пирамида нам дана правильная, значит что лежит в основании? (правильный треугольник)
-Чем тогда является отрезок CM? (медианой и высотой)

-Что из этого следует? (СМ перпендикулярна АВ)

-Когда прямая перпендикулярна плоскости? ( когда она перпендикулярна двум пересекающимся прямым, лежащим в плоскости)
-Какая прямая в плоскости сечения пересекается с СМ и тоже перпендикулярна АВ? (DO)

-Какой вывод мы тогда можем сделать? (АВ перпендикулярна CDO, следовательно перпендикулярна α)

-Нам дано что CH перпендикулярна DM. В какой плоскости лежит CH?( в плоскости α)

-А что мы доказали в предыдущем пункте? (АВ перпендикулярна α)

-Свяжем все три вывода вместе. Запишем решение. (CH перпендикулярна DM, АВ перпендикулярна α, CH принадлежит плоскости α, из этого следует что AB перпендикулярна CH.)
-Мы уже повторяли, когда прямая перпендикулярна плоскости. Найдем две пересекающиеся прямые, лежащие в плоскости, которые перпендикулярны прямой СH. (DM и AB)
- Какой можем сделать вывод? (CH перпендикулярна ADB, ч.т.д.)

№ 258

№ 255

№ 265

Рефлексивно-оценочная часть.

• какова была цель урока? (решить задачи на тему «правильная пирамида», закрепить материал)
• - достигли мы ее? (да)
• - как достигли? (повторили теорию, решили задачи)