Российской Федерации
Тюменский областной государственный институт
Развития регионального образования
Всероссийская олимпиада по математике 2011-2012 учебного года
Муниципальный этап
9 класс
1. Пятизначное число, являющееся полным квадратом, записывается с помощью цифр 0, 4, 8, 8, 8. Найдите это число.
(7 баллов)
2. Когда первый и второй спортсмены бегут по стадиону в одну сторону, то первый обгоняет второго раз в 15 минут, а когда они бегут навстречу, то встречаются один раз в 5 минут. Во сколько раз скорость первого бегуна больше скорости второго бегуна?
(7 баллов)
3. В параллелограмме АВСD выбрали произвольную точку К на стороне АВ. Точку пересечения отрезков АС и DК обозначили F. При этом 
и 
. Найдите площадь параллелограмма АВСD.
(7 баллов)
4. Найдите все значения х, при которых большее из чисел 3 х – 1 и х + 5 меньше 14.
(7 баллов)
5. По кругу записано n целых чисел, сумма которых равна 94. Известно, что любое число равно модулю разности двух следующих за ним чисел. Найдите все возможные значения n.
(7 баллов)
Всероссийская олимпиада по математике 2011-2012 учебного года
Муниципальный этап
Решения
9 класс
1. Пятизначное число, являющееся полным квадратом, записывается с помощью цифр 0, 4, 8, 8, 8. Найдите это число.
(7 баллов)
Решение:
Квадраты чисел не могут оканчиваться цифрами 2, 3, 7, 8!
Если квадрат натурального числа оканчивается 0, то само число делится на 10; но тогда квадрат должен оканчиваться двумя нулями. Следовательно, искомое число не оканчивается на 0. Кроме того, квадрат числа не может оканчиваться на 8, так что последняя цифра числа а равна 4. Но тогда остается рассмотреть числа 88804, 88084, 80884, из которых только первое является полным квадратом. Итак, а = 88804.
Ответ: 88804.
2. Когда первый и второй спортсмены бегут по стадиону в одну сторону, то первый обгоняет второго раз в 15 минут, а когда они бегут навстречу, то встречаются один раз в 5 минут. Во сколько раз скорость первого бегуна больше скорости второго бегуна?
(7 баллов)
Решение:
Пусть х м/мин – скорость первого спортсмена, у м/мин – скорость второго спортсмена, а м – длина окружности. По условию задачи составим 2 уравнения:
5 х + 5 у = а, 15 х – 15 у = а.
Приравнивая левые части уравнений, получаем зависимость между переменными х и у.
15 х – 15 у = 5 х + 5 у,
10 х = 20 у, х = 2 у.
Последнее равенство доказывает, что скорость первого бегуна в два раза больше скорости второго бегуна.
Ответ: в 2 раза.
3. В параллелограмме АВСD выбрали произвольную точку К на стороне АВ. Точку пересечения отрезков АС и DК обозначили F. При этом и . Найдите площадь параллелограмма АВСD.
(7 баллов)
Решение:
Рассмотрим 
и 
. Угол 
равен углу 
, так как эти углы вертикальные, а угол KAF равен углу DCF как внутренние накрест лежащие при параллельных АВ || СD и секущей АС. Поэтому подобен (по двум углам).
и . Треугольники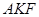 
и AFD имеют общую вершину А, и их основания KF и FD расположены на одной прямой. Площади таких треугольников относятся как соответственные стороны. Значит, KF: FD = 2: 7. Таким образом, коэффициент подобия и равен 
. Известно, что отношение площадей подобных треугольников равняется квадрату коэффициента подобия. Получаем:
: 
= 4: 49, 2: = 4: 49. Откуда получаем = 24,5.
= 7 + 24,5 = 31,5.
Диагональ АС делит параллелограмм АВСD на два равных треугольника, поэтому 
.
Ответ: 63.
4. Найдите все значения х, при которых большее из чисел 3 х – 1 и х + 5 меньше 14.
(7 баллов)
Решение:
Рассмотрим два случая.
1) Пусть 
. Решая это неравенство, получаем: 
.
Здесь большим из чисел 3 х – 1 и х + 5 является 3 х – 1. Будем иметь:
3 х – 1 < 14, х < 5.
Общей частью двух промежутков 
и 
является промежуток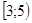 
.
2) Пусть 3 х – 1 < х + 5. Отсюда х < 3.
Теперь получаем:
х + 5 < 14, х < 9.
Общая часть интервалов 
и 
есть интервал .
Ответ: .
Рекомендации к выставлению оценки