Основные понятия статики
Материальная точка – тело, размерами которого можно пренебречь в условии данной задачи.
Абсолютно твердое тело – тело, в котором расстояние между любыми двумя точками всегда остается неизменным.
Сила – мера механического действия одного материального тела на другое.
Характеристики силы:
1) Точка приложения;
2) Направление действия;
3) Числовое значение (модуль).
F
Единицы измерения: [Н], [кН].
Система сил – несколько сил, действующих на одно твердое тело.

Свободные и несвободные тела. Связи. Классификация связей
Свободным называется тело, которое не скреплено с другими телами и может перемещаться в пространстве.
Пример: самолет, летящий в воздухе; воздушный шар в полете
Несвободным называется тело, перемещение которого в пространстве ограничено другими телами.
Связями называются тела, ограничивающие свободу перемещения данного тела.
Пример: вал, лежащий на подшипниках (вал – несвободное тело, подшипник - связь.
Классификация связей
1 тип: связи препятствуют перемещению тела в одном направлении
1) Гладкая поверхность


2) Опорная точка

3) Гибкая нерастяжимая нить

4) Прямолинейный стержень

5) Шарнирно – подвижная опора

2 тип: связи препятствуют перемещению тела по нескольким направлениям
Шарнирно - неподвижная опора

3 тип: связи препятствуют перемещению тела по нескольким направлениям и повороту вокруг своей оси
Заделка

Проекция силы на ось
Проекцией силы на ось называется отрезок, лежащий на оси между двумя перпендикулярами, проведенными на ось из начала и конца вектора силы.

Проекция силы на ось равна произведению модуля силы на cos угла между направлением силы и положительным направлением оси.

Правила знаков:
1) Если направление проекции силы совпадает с положительным направлением оси, то эта проекция положительна.

x
2) Если направление проекции силы противоположно положительному направлению оси, то эта проекция отрицательна.

х
3) Если вектор силы параллелен оси, то его проекция на эту ось равна самой силе.

Х
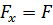
4) Если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю.

х

Плоская система сходящихся сил. Условия равновесия в аналитической и геометрической форме
Плоской системой сходящихся сил называется система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке.



Геометрический способ определения равнодействующей – построение силового многоугольника: в произвольно выбранную точку переносится объект равновесия, в эту точку помещается начало первого вектора, перенесенного параллельно самому себе; к концу первого вектора переносится начало второго вектора, к концу второго – начало третьего и т. д.
Геометрическое условие равновесия: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.

Аналитическое условие равновесия: для равновесия свободного твердого тела под действием плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех на каждую из осей координат была равна нулю
S Fix=0 SX=0
или
S Fiy=0 SY=0