Ход занятия:
1. Организованный момент. Приветствие учащихся. Сообщение темы и целей занятия. Проверка готовности студентов к занятию.
2. Актуализация
Вычислить: 1) 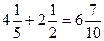 , 2)
, 2) 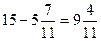 , 3)
, 3) 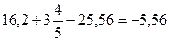
3. Объяснение нового материала:
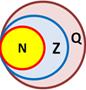
| Множество натуральных чисел | Определение: числа, которые мы используем при счете предметов, называются натуральными. При сложении и умножении натуральных чисел всегда получаются натуральные числа.
Утверждение: разность и частное натуральных чисел не всегда являются натуральными числами.
Натуральные числа используются при счете предметов. 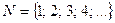

|
| Множество целых чисел | Дополним множество натуральных чисел, нулем и отрицательными числами.Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа. Однако частное двух целых чисел, не обязятельно будет целым числом.
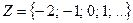
|
| Множество рациональных чисел | Введение рациональных чисел, то есть чисел вида 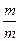 , где , где 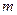 – целое число, – целое число, 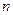 – натуральное число, дает возможность находить частное двухрациональных чисел при условии, что делитель не равен нулю.
Каждое целое число – натуральное число, дает возможность находить частное двухрациональных чисел при условии, что делитель не равен нулю.
Каждое целое число 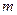 также является рациональным, так как его можно представить в виде также является рациональным, так как его можно представить в виде 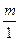 .
Утверждение: при выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа. .
Утверждение: при выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.
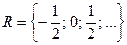
|
| Конечные десятичные дроби | Если рациональное число можно представить в виде дроби 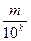 , где , где 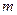 – целое число, – целое число, 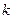 – натуральное число, то его можно записать в виде конечной десятичной дроби.
Например, – натуральное число, то его можно записать в виде конечной десятичной дроби.
Например, 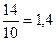 . .
|
| Бесконечные десятичные дроби | Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби.
Если, например, попытаться записать число 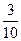 в виде десятичной дроби, разделив числитель на знаменатель, то получится бесконечная десятичная дробь в виде десятичной дроби, разделив числитель на знаменатель, то получится бесконечная десятичная дробь 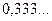 Бесконечную деятичную дробь
Бесконечную деятичную дробь 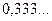 называют периодической, а повторяющуюся цифру 3 - ее периодом.
Коротко записывают так: называют периодической, а повторяющуюся цифру 3 - ее периодом.
Коротко записывают так: 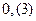 (ноль целых три десятых в периоде) (ноль целых три десятых в периоде)
|
| Бесконечная периодическая десятичная дробь | Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби.
Например, 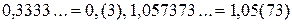 Утверждение. Каждая бесконечная периодическая дробь является рациональным числом, так как может быть представлена в виде
Утверждение. Каждая бесконечная периодическая дробь является рациональным числом, так как может быть представлена в виде 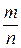 , где , где 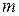 - это целое число, - это целое число, 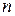 - натуральное число. - натуральное число.
|
4. Решение ключевых задач.
1. Представить в виде десятичной дроби 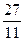
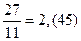
2) Записать бесконечную периодическую дробь 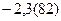 в виде обыкновенной дроби.
в виде обыкновенной дроби.
Решение. Распишем период дроби: 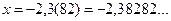
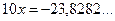
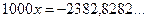
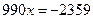
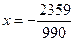
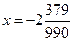
Ответ: 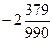 .
.
3) Записать бесконечную периодическую дробь 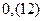 в виде обыкновенной дроби.
в виде обыкновенной дроби.
Решение. Распишем период дроби: 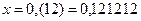
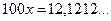
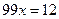
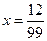 ,
, 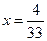
Ответ: 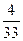 .
.
5. Решение упражнений.
1) Записать в виде десятичной дроби:
1) 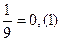 ; 2)
; 2) 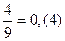 ; 3)
; 3) 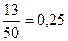 ; 4)
; 4) 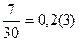 ; 5)
; 5) 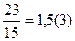 .
.
2) Выполнить действия и записать результат в виде десятичной дроби:
1) 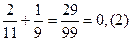 , 2)
, 2) 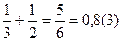
3) Представить в виде обыкновенной дроби:
1) 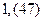
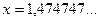
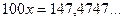
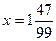 .
.
2) 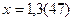
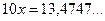
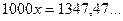
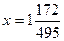 .
.
3) 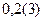
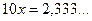
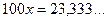
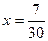 .
.
4) 0,2(18)
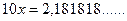
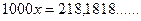
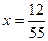 .
.
1) Представить обыкновенную дробь в виде десятичной периодической дроби
1. 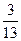 ; 2.
; 2. 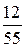 ; 3.
; 3. 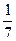 ; 4.
; 4. 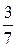 ;
;
5. 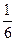 ; 6.
; 6. 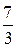 ; 7.
; 7. 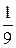 ; 8.
; 8. 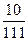 ;
;
9. 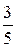 ; 10.
; 10. 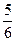 ; 11.
; 11. 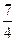 ; 12.
; 12. 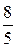 .
.
2) Записать в виде обыкновенной дроби бесконечную периодическую десятичную дробь
1. 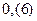 ; 2.
; 2. 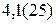 ; 3.
; 3. 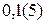
4. 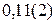 ; 5.
; 5. 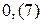 ; 6.
; 6. 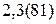 ;
;
7. 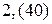 ; 8.
; 8. 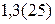 ; 9.
; 9. 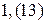 ;
;
10. 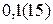 ; 11.
; 11. 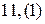 ; 12.
; 12. 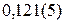 ;
;
3) Найти значение следующих дробей
1. 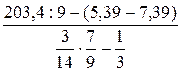 .
.