ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7.
Соединения – это множества, составленные из каких-либо предметов (элементов). Наиболее часто используются три вида соединений: размещения, перестановки и сочетания.
Размещения (от франц. аrrangement – размещение) из n элементов по m – это соединения, в каждое из которых входит m элементов, взятых из данных n элементов и которые отличаются между собой элементами (хотя бы одним) или их порядком. Число возможных размещения  вычисляют по формуле:
вычисляют по формуле:
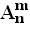 =n ∙ (n - 1) ∙ (n-2)….(n - (m - 1))
=n ∙ (n - 1) ∙ (n-2)….(n - (m - 1))
Например:  =8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 = 6720
=8 ∙ 7 ∙ 6 ∙ 5 ∙ 4 = 6720
Перестановки из n элементов по m – это соединения, каждое из которых содержит все n элементов и которые отличаются лишь порядком элементов. Число возможных перестановок  вычисляют по формуле:
вычисляют по формуле:
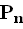 = n! = 1 ∙ 2 ∙ 3∙…..∙ (n – 1) ∙ n
= n! = 1 ∙ 2 ∙ 3∙…..∙ (n – 1) ∙ n
Например:  = 5! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5=120
= 5! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5=120
Сочетания из элементов по m (m  n) – это такие соединения, в каждое из которых входят m элементов, взятых из данных n элементов и отличающиеся элементами (хотя бы только одним). Число возможных сочетаний вычисляются по формуле:
n) – это такие соединения, в каждое из которых входят m элементов, взятых из данных n элементов и отличающиеся элементами (хотя бы только одним). Число возможных сочетаний вычисляются по формуле:
 =
=  =
= 
Например:  =
=  =
=  = 495
= 495
Принимают, что 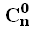 = 1, 0! = 1 и 1! = 1
= 1, 0! = 1 и 1! = 1
1. Из десяти спортсменов отбирают команду из 6-ти человек. Это можно сделать … способами.
1) 210 2) 60 3) 3
2. В команде всего 12 спортсменов, из них 5 человек – мастера спорта. Случайным образом выбирают 3-х спортсменов. Вероятность того, что все выбранные окажутся мастерами спорта, составляет …
1) 1/22 2) 3/5 3) 1/4
3. В ящике 10 одинаковых деталей, помеченных номерами: №1, №2,….№10. Наудачу берут 6 деталей. Вероятность того, что среди выбранных 6-ти деталей окажется деталь с №1, составляет …
1) 0,6 2) 1/6 3) 0,1 4) 0,15
4. В ящике 10 одинаковых деталей, помеченных номерами: №1, №2, …, №10. Наудачу берут 6 деталей. Вероятность того, что среди этих 6-ти есть детали №1 и № 2, составляет …
1) 2/5 2) 1/3 3) 1/6 4) 1/4
5. На книжной полке случайным образом расставляют 6 учебников. Вероятность того, что учебник математики и учебник русского языка окажутся рядом, составляет …
1) 0,36 2) 0,72 3) 1/3
6. В группе спортсменов 10 человек, все разного роста. По команде тренера они выстраиваются в шеренгу случайным образом. Вероятность того, что они встали по росту, составляет…
1) 0,6  2) 0,2 3) 0,1
2) 0,2 3) 0,1
7. В ящике 4 красных и 2 синих шара. Из него наудачу берут 3 шара. Вероятность того, что все эти 3 шара красные, составляет…
1) 3/4 2) 1/2 3) 1/4 4) 1/5
8. В лотерее «Честная игра» нужно открыть 10 букв из 20-ти, если открываются буквы, составляющие слово «автомобиль», - то это выигрыш. Вероятность выигрыша составляет …
1) 0,5 2) 0,01 3) 0,5∙ 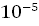
9. Выбирают 2-х игроков из 4-х заявленных на матч. Это можно сделать... способами.
1) 6 2) 2 3) 4
10. Из группы 5 человек (№1, №2, №3, №4, №5) выбирают случайным образом двух человек. Вероятность того, что выбраны №1 и №4, составляет…
1) 2/5 2) 1/5 3) 1/10
11. Имеется слово «автор». Из букв этого слова можно составить некоторое число различных последовательностей (не обязательно осмысленных):
1) 25 2) 120 3) 6
12. Из букв слова «фонарь» можно составить некоторое число последовательностей (не обязательно осмысленных):
1) 20 2) 120 3) 720
13. В корзине 20 кубиков, помеченных номерами 21, 22,…,40 (20 штук). Наудачу извлекают два кубика. Вероятность того, что извлечены кубики №21 и № 40, составляет…
1) 1/190 2) 2/20 3) 1/5
14. В корзине имеется 15 шаров, из которых 10 окрашенных. Наудачу извлекают 3 шара. Вероятность того, что извлеченные шары окажутся окрашенными, составляет…
1) 2/3 2) 3/10 3) 24/91
15. В конверте имеются 100 фотографий. Наудачу извлекают 10 штук. Вероятность того, что среди этих 10 штук окажется разыскиваемая одна фотография, составляет …
1) 0,1 2) 0,01 3) 0,0001
16. Набирая номер телефона, абонент забыл последние три цифры, но помнил, что эти три цифры различны, поэтому набрал их наудачу. Вероятность того, что он набрал нужные цифры, составляет …
1) 1/720 2) 0,3 3) 0,03
17. В корзине 100 шаров, из них 10 окрашенных. Наудачу взяли 4 шара. Вероятность того, что среди взятых шаров нет окрашенных, составляет …
1) 0,96 2) 0,65 3) 0,04
18. В корзине 100 шаров, из них - 10 окрашенные. Наудачу взяли 4 шара. Вероятность того, что все они окрашенные, составляет …
1) 0,4 2) 0,04 3) 0,00005
19. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрывают 4 билета на концерт. Вероятность того, что обладателями билетов будут 2 женщины и 2 мужчин, составляет…
1) 2/3 2) 18/35 3) 1/2 4) 4/7
20. В ящике 8 красных и 7 синих шаров. Вынимают наудачу 5 шаров. Вероятность того, что взяли 3 красных и 2 синих (из этих 5-ти), составляет…
1) 0,3 2) 0,211 3) 0,392
| Тест № | Пояснения | Ответ |
| 1. | Вычислим число сочетаний t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>6</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  :
t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>6</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> :
t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>6</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  = =  = =  = =  = 210 = 210
| |
| 2. | Всего способов выбора из 12-ти 3-х равна:
t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>3</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  = =  = =  = =  = 220
Количество возможных способов выбора из 5-ти человек трех: = 220
Количество возможных способов выбора из 5-ти человек трех:  = =  = =  = 10
Искомая вероятность: р = = 10
Искомая вероятность: р =  = =  = = 
| 
|
| 3. | Общее число исходов равно числу способов, которыми можно извлечь 6 деталей из 10-ти, т.е. t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>6</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>6</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>6</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  = =  = = 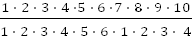 = 210
Интересующее событие – деталь №1 извлечена, тогда остальные 5 деталей имеют любые номера, число таких способов равно = 210
Интересующее событие – деталь №1 извлечена, тогда остальные 5 деталей имеют любые номера, число таких способов равно 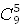 = =  = 126.
Искомая вероятность: р (№1) = = 126.
Искомая вероятность: р (№1) =  = 0,6 = 0,6
| 0,6 |
| 4. | Общее число исходов  Если среди взятых 6-ти есть №1 и №2, то число способов, которыми можно взять еще 4 детали из оставшихся 8-ми:
Если среди взятых 6-ти есть №1 и №2, то число способов, которыми можно взять еще 4 детали из оставшихся 8-ми:  = 70, т.е. искомая вероятность: р (№1, №2) = = 70, т.е. искомая вероятность: р (№1, №2) =  = = 
| 
|
Общее число возможных вариантов расположения 6-ти книг на полке равно
 = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 6! = 720
Благоприятные исходы могут быть 2х видов:
1) Если учебник математики стоит на краю, а учебник русского – рядом, таких вариантов два, а оставшиеся 4 места можно занять 4! Способами, т.е. всего таких исходов будет: 2∙4!=48
2) Если учебник математики находится в середине (а таких способов 4), тогда учебник русского языка можно поставить рядом (справа или слева), т.е. двумя способами, а остальные 4 места можно занять 4! способами. Итого благоприятных условий в этом виде расстановки будет: 4 ∙ 2 ∙ 4! = 192
Всего благоприятных исходов будет
48 + 192 = 240
Искомая вероятность: р = = 1∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 6! = 720
Благоприятные исходы могут быть 2х видов:
1) Если учебник математики стоит на краю, а учебник русского – рядом, таких вариантов два, а оставшиеся 4 места можно занять 4! Способами, т.е. всего таких исходов будет: 2∙4!=48
2) Если учебник математики находится в середине (а таких способов 4), тогда учебник русского языка можно поставить рядом (справа или слева), т.е. двумя способами, а остальные 4 места можно занять 4! способами. Итого благоприятных условий в этом виде расстановки будет: 4 ∙ 2 ∙ 4! = 192
Всего благоприятных исходов будет
48 + 192 = 240
Искомая вероятность: р =  = = 
| 
| |
| 6. | Общее число равновозможных событий равно числу перестановок из 10 спортсменов:  = 10!=3268800
Ученики по росту могут встать двумя способами: по возрастанию или по убыванию, т.е. событию «встали по росту» благоприятствует два исхода, тогда:
р = = 10!=3268800
Ученики по росту могут встать двумя способами: по возрастанию или по убыванию, т.е. событию «встали по росту» благоприятствует два исхода, тогда:
р =  = = 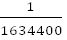 ≈ 0,6 ∙ ≈ 0,6 ∙ 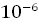
| 0,6 
|
| 7. | Вероятность этого события равна:
р =  = = 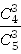 = = 
| 
|
| 8. | р =  = =  = 0,05∙ = 0,05∙ 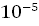
| 0,5 ∙ 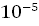
|
| 9. | Это:  = =  = 6 = 6
| |
| 10. | Всего возможностей выбора:  = 10 способов. Событию (выбран №1 + №4) соответствует только один исход. Вероятность этого составляет р = = 10 способов. Событию (выбран №1 + №4) соответствует только один исход. Вероятность этого составляет р = 
| 0,1 |
| 11. | Это перестановки из 5-ти букв слова «Автор»:
 = 5! = 120 = 5! = 120
| |
| 12. | Это перестановки из 6-ти букв слова «Фонарь»:
 = 6! = 720 = 6! = 720
| |
| 13. | Надо взять два кубика из 20-ти. Это можно сделать 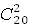 способами: способами:
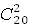 = = 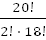 = =  = 190
Благоприятное событие 1 (взяты №21 и №40), поэтому р = = 190
Благоприятное событие 1 (взяты №21 и №40), поэтому р = 
| 
|
| 14. | Искомая вероятность будет:
р =  = =  р =
р =  = = 
| 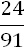
|
| 15. |  - число способов, которыми из 100 фотографий можно взять 10 любых.
Если среди взятых 10-ти фотографий есть та, которая нужна, то остальные 9 фотографий могут быть любыми. Это можно сделать числом способов: t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>9</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> - число способов, которыми из 100 фотографий можно взять 10 любых.
Если среди взятых 10-ти фотографий есть та, которая нужна, то остальные 9 фотографий могут быть любыми. Это можно сделать числом способов: t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>9</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  .
Тогда p = .
Тогда p =  = =  = 0,1 = 0,1
| 0,1 |
| 16. | Благоприятный исход только один – набраны нужные цифры и в нужной последовательности.
Всего возможных исходов:  , т.к. цифр 10-ть, а размещения учитывают порядок цифр и их состав.
Тогда p = , т.к. цифр 10-ть, а размещения учитывают порядок цифр и их состав.
Тогда p =  = = 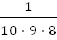 = = 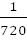
| 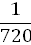
|
| 17. |  - число способов, которыми можно взять 4 шара из 100 шт. t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>4</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> - число способов, которыми можно взять 4 шара из 100 шт. t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>4</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  – число способов, которыми можно взять 4 шара из 90 шт.
p = s w:val="32"/></w:rPr></m:ctrlPr></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> – число способов, которыми можно взять 4 шара из 90 шт.
p = s w:val="32"/></w:rPr></m:ctrlPr></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 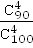 ≈ 0,65 ≈ 0,65
| 0,65 |
| 18. | p = s w:val="32"/></w:rPr></m:ctrlPr></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 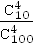 ≈ 0,00005 ≈ 0,00005
| 0,00005 |
| 19. | Всего пойдут на концерт 4 человека из 7, такой выбор можно сделать  = =  = 35 способами.
Из 4-х женщин 2-х можно выбрать = 35 способами.
Из 4-х женщин 2-х можно выбрать  = 6 способами.
Из 3-х мужчин 2-х можно выбрать = 6 способами.
Из 3-х мужчин 2-х можно выбрать  = 3 способами. Следовательно:
p = = 3 способами. Следовательно:
p =  = = 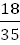
| 
|
| 20. | Общее число событий: t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>5</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 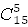 = 3003. Выбрать 3 красных из 8-ми: = 3003. Выбрать 3 красных из 8-ми: 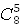 = 56 способов. Выбрать 2 синих из 7-ми: = 56 способов. Выбрать 2 синих из 7-ми:  = 21 способов. Общее число благоприятных событий: = 21 способов. Общее число благоприятных событий:  =1176. Вероятность: p = =1176. Вероятность: p =  ≈ 0,392 ≈ 0,392
| 0,392 |