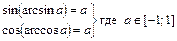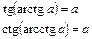Формулы тройных углов
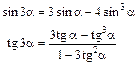
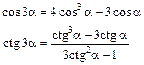
Обратные тригонометрические функции
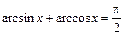
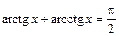
Некоторые значения тригонометрических функций
таблица 3
| Аргумент | Функция | |||
| sin a | cos a | tg a | ctg a | |
15°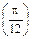 
| 
| 
| 
| 
|
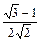
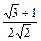
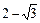
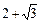
18°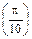 
| 
| 
| 
| 
|
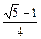
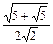
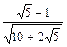
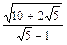
36°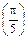 
| 
| 
| 
| 
|
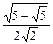
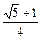
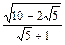
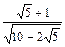
54°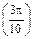 
|
|
|
|
|
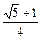
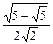
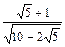
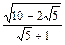
72°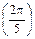 
|
|
|
|
|
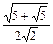
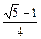
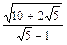
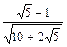
75°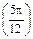 
|
|
|
|
|
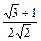
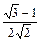
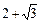
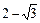
Алгебраические функции — это функции, заданные аналитическим выражением, в записи которого используются алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
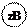у = 2 х + 3,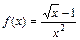 
Числовая прямая — это математическая модель для представления чисел, в которой каждое число соответствует точке на прямой, причем расстояние от точки до начала отсчета равно модулю числа:
 |
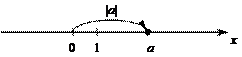Признаки числовой прямой:
1) начало отсчета;
2) единичный отрезок;
3) положительное направление (стрелка).
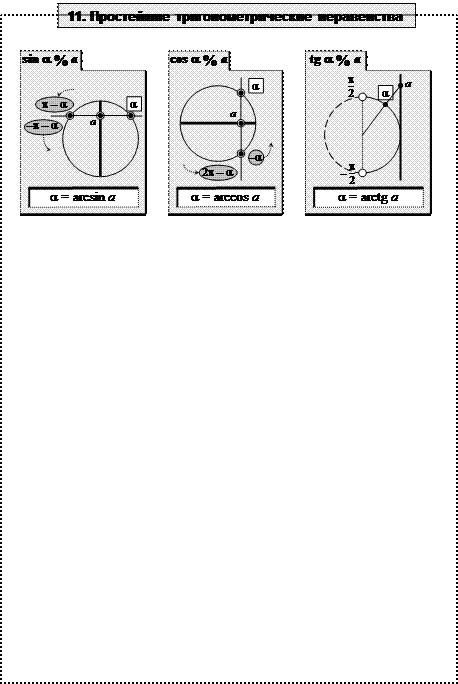
Чтобы решить простейшее тригонометрическое неравенство нужно:
1. Провести прямую к линии соответствующей функции.
2. Выделить дугу, на которой лежат решения неравенства.
3. Найти концы этой дуги, помня, что обход совершается против часовой стрелки от меньшего числа к большему.
4. Прибавить к концам интервала числа, кратные периоду функции.
Решить неравенство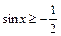 
.
Решение.
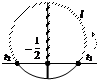Все решения, удовлетворяющие заданному неравенству, лежат на дуге l. Найдем ее концы:
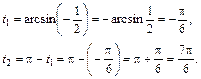
С учетом периода синуса, запишем ответ:
.
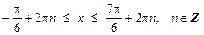Ответ: 
Если правая часть уравнения — отрицательное число, то следует воспользоваться свойствами соответствующих обратных тригонометрических функций, тогда:
 |
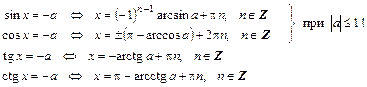
При а = 1; 0; –1 решение уравнения записывается в виде (n Î Z):
|
|
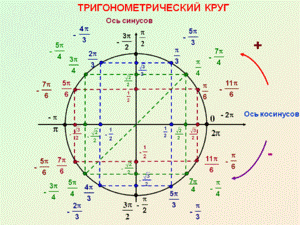
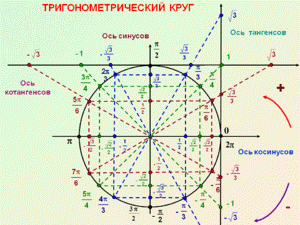
Единичная окружность — это окружность, радиус которой принят за единицу измерения.
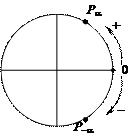
Числовая окружность — это единичная окружность с установленным соответствием между действительными числами и точками окружности:
 | |||||
 | |||||
 | |||||
Указанное соответствие можно определить следующим образом: каждому числу a соответствует такая точка Р числовой окружности, чтобы дуга È ОР имела длину |a| и была отложена в положительном направлении если a > 0 и в отрицательном, если a < 0:
Признаки числовой окружности:
1) начало отсчета – правый конец горизонтального диаметра;
2) единичный отрезок – длина радиуса окружности;
3) положительное направление – против часовой стрелки.
 |
Откладывать можно дуги какой угодно длины. То есть числовую окружность можно рассматривать как окружность радиуса 1, на которую «намотана» числовая прямая:
 |
Угол в 1 ° — это центральный угол, опирающийся на дугу, длина которой равна части окружности.
Угол поворота — это угол, полученный вращением луча около его начала О от начального положения ОА до конечного положения ОВ.
Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
 |
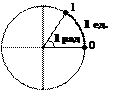
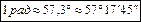
Радианная мера угла численно равна пути, который проходит точка по дуге единичной окружности, на которую опирается этот угол:
Для связи радианов и градусов используют развернутый угол:
 |
|
|
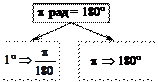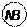1. Говорят: «угол радиан» или чаще «угол ». Обозначение «радиан» или «рад», как правило, опускают.
2. Термин «радианное измерение углов» равносилен термину «числовое измерение углов», т.е. фраза «угол a равен двум радианам» равносильна фразе «угол a равен числу 2» и даже «угол a равен двум». Поэтому вопрос типа «Чему равно?» некорректен. Нужно спрашивать: «Чему равен угол?» (60°) или «Чему равно число?» (» 1,05).
Арксинусом числа а называется такое число х из интервала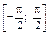 
, синус которого равен а.
 |
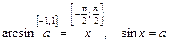
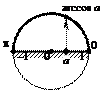Арккосинусом числа а называется такое число х из интервала [0; p], косинус которого равен а.
 |
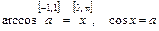
Арктангенсом числа а называется такое число х из интервала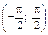 
, тангенс которого равен а.
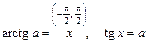
Арккотангенсом числа а называется такое число х из интервала (0; p), котангенс которого равен а.
 |
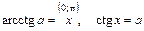
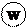1. Для отрицательных значений аргумента:
 |
2. Из определения аркфункции сразу следует, что:
|
VI. Формулы половинного аргумента (знак – по функции в левой части):
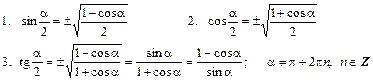
VII. Формулы сумм:
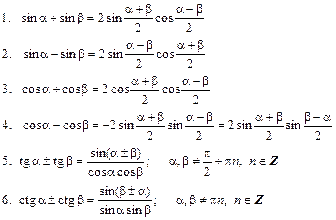
VIII. Формулы произведений:
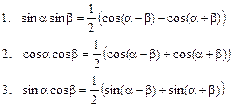
IX. Универсальная тригонометрическая подстановка:
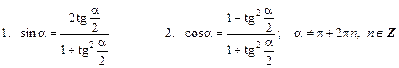
X. Некоторые дополнительные формулы:
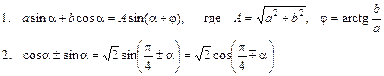
á Полный ñ оборот — это угол поворота, равный 2p рад (или 360°).
 | |||
 |
Некоторые положения конечной точки угла поворота:
 |
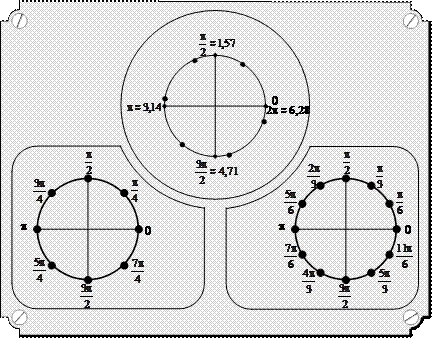Функция косинус — это функция, которая ставит в соответствие каждому числу t абсциссу точки М (t) координатной окружности.
|
|
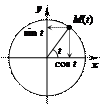Функция синус — это функция, которая ставит в соответствие каждому числу t ординату точки М (t) координатной окружности.
Если М (t) = М (х; у),
то х = cos t, у = sin t
Таким образом,
М (t) = М (cos t; sin t)
 |
Запись М(t) показывает положение точки М на координатной окружности, а запись М(cos t; sin t) – положение той же точки на координатной плоскости.
Функция тангенс — это частное от деления функции синус на функцию косинус.
Функция котангенс — это частное от деления функции косинус на функцию синус.
 |
Поскольку деление на нуль невозможно, функции tg t и ctg t определены не для всех значений аргумента. Тангенс определен лишь для значений аргумента, при которых cos t ¹ 0, котангенс определен при sin t ¹ 0:
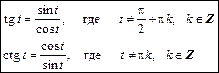
Тригонометрические функции — это общее название функций синус, косинус, тангенс и котангенс.
I. Основное тригонометрическое тождество и следствия из него:
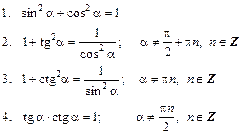
II. Формулы (теоремы) сложения аргументов:
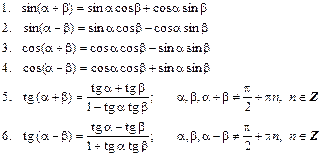
III. Формулы приведения:
1) функция меняется на кофункцию при переходе через вертикальную ось и не меняется при переходе через горизонтальную;
2) перед приведенной функцией ставится знак приводимой функции, считая a углом первой четверти.
IV. Формулы двойного аргумента:
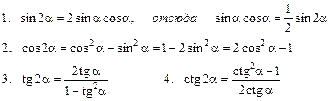
V. Формулы понижения степени:
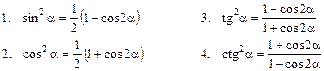
Значения тригонометрических функций
некоторых углов
таблица 1
| p | |||||||
| sin a |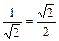 
| 
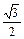
| –1 | ||||
| cos a |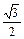
|
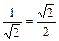
| –1 | ||||
| tg a |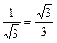 
| 
| — | — | |||
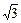
| ctg a | — |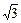
|
| — |
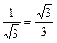
Связь между тригонометрическими функциями
одного аргумента
таблица 2
| Искомая функция | Выражение искомой функции через | |||
| sin a | cos a | tg a | сtg a | |
| sin a = | sin a |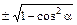 
| 
| 
|
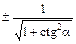
| cos a = |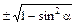 
| cos a |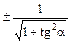 
| 
|
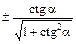
| tg a = |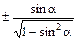 
| 
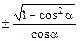
| tg a |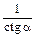 
|
| сtg a = |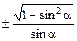 
| 
| 
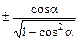
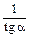
| сtg a |
|
Тригонометрический набор координат:
 |
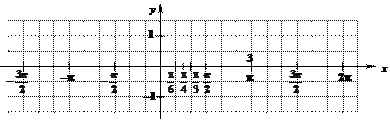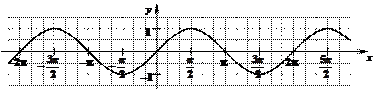у = sin x синусоида
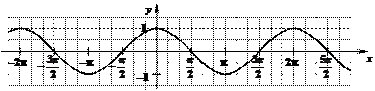у = cos x á ко ñ синусоида
у = tg x у = ctg x
тангенсоида á ко ñ тангенсоида
 |
|
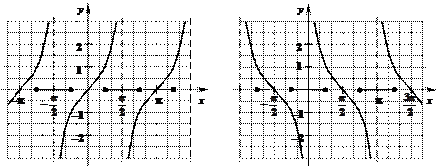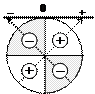
| Линия синусов | Область значений | Знаки по четвертям | Четность – нечетность |
| |||
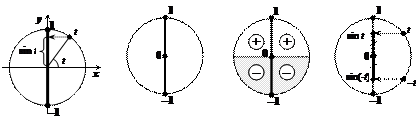
| |sin t | £ 1 | sin(– t) = –sin t |
| Линия косинусов | Область значений | Знаки по четвертям | Четность – нечетность |
| |||
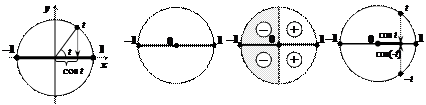
| |cos t | £ 1 | cos(– t) = cos t |
| Область определения | |
| D (sin) = R | D (cos) = R |
| Область значений | |
| E (sin) = [–1; 1] | E (cos) = [–1; 1] |
| Четность – нечетность | |
| нечетная функция | четная функция |
| Периодичность | |
| sin(x ± 2p) = sin x | cos(x ± 2p) = cos x |
|
| Линия тангенсов | Область значений | Знаки по четвертям | Четность – нечетность |
| |||
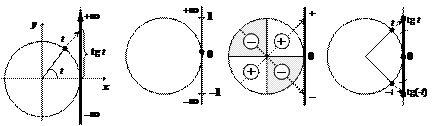
| tg t Î (–¥; +¥) | tg(– t) = –tg t |
| Линия котангенсов | Область значений | Знаки по четвертям | Четность – нечетность |
| 
| 
| 
|
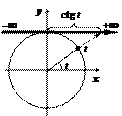
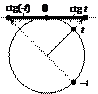
| ctg t Î (–¥; +¥) | ctg(– t) = –ctg t |
| Область определения | |
| 
|
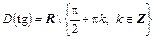
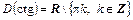
| Область значений | |
| E (tg) = (–¥; +¥) | E (ctg) = (–¥; +¥) |
| Четность – нечетность | |
| нечетная функция | нечетная функция |
| Периодичность | |
| tg(x ± p) = tg x | ctg(x ± p) = ctg x |
