Постановка задачи. Дана тренировочная коллекция. Каждый объект представляется ввиде набора n характеристик = n-мерный вектор. Необходимо построить классифицирующее правило.
Предпосылки Считаем, что элементы каждой категории имеют свое распределение в n-мерном пространстве. Будем принимать решение по правилу Байеса! Но для этого необходимо знать функции распределения каждой категории. Далее возможные 2 варианта:
· функции распределениея нам известны;
· нам известен тип распределения, но не параметры;
1. Функции распределения известны Просто используем правило Байеса.
2. Известен тип, но не параметры.Будем использовать точечные оценки для параметров распределения. Пример. В случае нормального распределения будем использовать: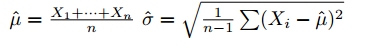 
Байесовский классификатор — широкий класс алгоритмов классификации, основанный на принципе максимума апостериорной вероятности(Апостерио́рнаявероя́тность — условная вероятность случайного события при условии того, что известны апостериорные данные, т.е. полученные после опыта. Априорный анализ. Исследователь выбирает такие нежелательные события, которые являются потенциально возможными для данной системы, и пытается составить набор различных ситуаций, приводящих к их появлению.
Апостериорный анализ. Выполняется после того, как нежелательное событие уже произошло. Цель такого анализа – разработка рекомендаций на будущее.).
Для классифицируемого объекта вычисляются функции правдоподобия каждого из классов, по ним вычисляются апостериорные вероятности классов. Объект относится к тому классу, для которого апостериорная вероятность максимальна.
Байесовский подход к классификации основан на теореме, утверждающей, что если плотности распределения каждого из классов известны, то искомый алгоритм можно выписать в явном аналитическом виде. Более того, этот алгоритм оптимален, то есть обладает минимальной вероятностью ошибок.
На практике плотности распределения классов, как правило, не известны. Их приходится оценивать (восстанавливать) по обучающей выборке. В результате байесовский алгоритм перестаёт быть оптимальным, так как восстановить плотность по выборке можно только с некоторой погрешностью. Чем короче выборка, тем выше шансы подогнать распределение под конкретные данные и столкнуться с эффектом переобучения.
К числу байесовских методов классификации относятся:
§ Наивный байесовский классификатор
§ Линейный дискриминант Фишера
§ Квадратичный дискриминант
§ Метод парзеновского окна
Основная формула
Пусть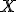 
— множество описаний объектов, 
— множество номеров (или наименований) классов. На множестве пар «объект, класс» 
определена вероятностная мера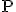 
. Имеется конечная обучающая выборка независимых наблюдений 
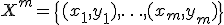, полученных согласно вероятностной мере .
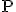Задача классификации заключается в том, чтобы построить алгоритм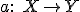 
, способный классифицировать произвольный объект 
.
В байесовской теории классификации эта задача разделяется на две.
§ Построение оптимального классификатора при известных плотностях классов. Эта подзадача имеет простое и окончательное решение.
§ Восстановление плотностей классов по обучающей выборке. В этой подзадаче сосредоточена основная сложность байесовского подхода к классификации.