Таб. 1
| № | Группировоч-ный признак | Результатив-ный признак | № | Группировоч-ный признак | Результатив-ный признак | |
| число вагонов находящихся в ремонте, шт/сут | чистая прибыль предприятия, млн.руб. | число вагонов находящихся в ремонте, шт/сут | чистая прибыль предприятия, млн.руб. | |||
Решение задачи:
1. Группировка производится по группировочному признаку. Определим величину (шаг) интервала группировки по формуле:



 k = 5, число групп в группировке (из условия)
k = 5, число групп в группировке (из условия)
Xmax, Xmin – максимальное и минимальное значение группировочного
признака
l – величина (шаг) интервала группировки.

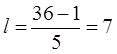
2. Определим нижнюю и верхнюю интервальные границы для каждой группы:
номер границы
группы нижняя верхняя
1 1.0 8.0
2 8.0 15.0
3 15.0 22.0
4 22.0 29.0
5 29.0 36.0
3. Составим рабочую таблицу, куда сведем первичный статистический материал:
| Группы предпри-ятий по кол-ву вагонов нахощящ. на ремонте, шт/сут | Номер предприятия | Число вагонов, находящихся в ремонте, шт/сут | Чистая прибыль предприятия, млн.руб. | |
| 1.0 - 8.0 |
 81 81
| |||
| ИТОГО: | ||||
| 8.0 - 15.0 | ||||
| ИТОГО: | ||||
| 15.0 - 22.0 | ||||
| ИТОГО: | ||||
| 22.0 - 29.0 | ||||
| ИТОГО: | ||||
| 29.0 - 36.0 | ||||
| ИТОГО: | ||||
4. Разработаем аналитическую таблицу взаимосвязи между числом вагонов находящихся на ремонте и чистой прибылью:

Табл. 2
| Группы предпр. по кол-ву вагонов поступающих в ремонт | Число предпри-ятий | Число вагонов находящихся в ремонте, шт/сут | Чистая прибыль, млн.руб | ||
| Всего по группе | в среднем на одно предприятие | Всего по группе | в среднем на одно предприятие | ||
| 1.0 - 8.0 | 4,2 | 126,2 | |||
| 8.0 - 15.0 | 11,4 | 138,3 | |||
| 15.0 - 22.0 | 18,0 | 153,5 | |||
| 22.0 - 29.0 | 26,3 | 158,0 | |||
| 29.0 - 36.0 | 36,0 | 155,0 |
Исследовав показатели работы 50-ти предприятий железнодорожного транспорта, можно сказать, что чистая прибыль предприятия находится в прямой зависимости от числа вагонов находящихся в ремонте.
Задание 2.
Рассчитать коэффициенты вариации по группировочному признаку на основании исходных данных и по аналитической группировке согласно своего варианта из задания 1. Объяснить (если есть) расхождения в значениях полученных коэффициентов.
Решение:
Расчет коэффициента вариации проводится по следующей формуле:


где: G – среднее квадратическое отклонение;
x - средняя величина

1) 
n – объем (или численность) совокупности,
х - варианта или значение признака (для интервального ряда принимается
среднее значение)
Рассчитаем показатели вариации для примера, рассмотренного в задании 1. Расчет проводится по группировочному признаку. Во-первых, рассчитаем все показатели по исх. данным (см. табл. 1):


2) Среднее кв. отклонение рассчитываем по формуле:



вернемся к форм. (1) 
3) Теперь рассчитаем коэффициент вариации по аналитической таблице (см. табл. 2)
Рассчитаем серединные значения интервалов:
4,5 11,5 18.5 25,5 32,5

1 8 15 22 29 36

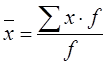 , где
, где
f - частота, т.е. число, которое показывает, сколько встречается каждая
варианта:
 ваг.
ваг.
Расчет среднего квадратического отклонения по аналитической группировке:


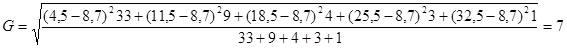

 Вывод: в обоих случаях расчета, коэффициент вариации (V) значительно больше 30 %. Следовательно, рассмотренная совокупность неоднородна и средняя для нее недостаточно типична.
Вывод: в обоих случаях расчета, коэффициент вариации (V) значительно больше 30 %. Следовательно, рассмотренная совокупность неоднородна и средняя для нее недостаточно типична.
Задание 3.
Провести 20 % механическую выборку из генеральной совокупности, представленной в таблице (использовать все 100 предприятий), по показателю, который является результативным признаком в аналитической группировке задания 1 в соответствии с вариантом. С вероятностью 0,997 рассчитать границы изменения средней величины в генеральной совокупности. Рассчитать среднюю данного признака по генеральной совокупности (по табл.) и сравнить с результатом, полученным на основании расчета по выборочной совокупности. Начало отбора начинать с номера предприятия совпадающего с номером варианта (8).
Табл.
| Номер предприятия | Чистая прибыль предпр., млн.руб. | Номер предприятия | Чистая прибыль предпр., млн.руб. | |
2) Для расчета границ изменения средней характеристики генеральной совокупности по материалам выборки воспользуемся формулами:

 (1)
(1)

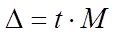 (2)
(2)

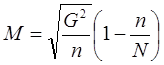 (3)
(3)
Х – средняя генеральной совокупности;
Х – средняя выборочной совокупности;
- 
 предельная ошибка выборки;
предельная ошибка выборки;
t - коэффициент доверия = 0,997 (по условию);
М – средняя ошибки выборки
G2 – дисперсия исследуемого показателя;
n – объем выборочной совокупности;
N – объем генеральной совокупности;
n/N – доля выборочной совокупности в объеме генеральной (или %
отбора, выраженный в коэффициенте)
Решение:
1) В данном варианте задания средняя чистая прибыль на одно предприятие по выборочной совокупности равна
Х=136,8 млн.руб.;
2) дисперсия равна = 407,46;
3) коэф-т доверия =3, т.к. вероятность определения границ средней равна =0,997 (по усл);
4) n/N = 0,2, т.к. процент отбора составляет 20 % (по условию).
5) Рассчитаем среднюю ошибку по ф. (3):

6) Рассчитаем предельную ошибку и определим границы изменения средней по ф. (2)

Т.о. с вероятностью 0,997 можно утверждать, что чистая прибыль на одно предприятие в генеральной совокупности будет находиться в пределах от 124,5 млн.руб. до 149,1 млн.руб., включая в себя среднюю по выборочной совокупности.
7) Теперь рассчитаем среднюю по генеральной совокупности (по 100 предприятиям) и сравним ее с полученной интервальной оценкой по выборке:


 |
где а1 + а2 +... +а100 – сумма числа вагонов, находящихся в ремонте
(штук в сутки) на 1, 2, 3...,100 предприятиях.
Вывод: Сравнивая среднюю генеральную совокупность равную 140,27 с интервальной оценкой по выборке 124,5 < x < 149,1 делаем выбор, что интервал с заданной вероятностью заключает в себе генеральную среднюю.
Задание 4.
По данным своего варианта (8) рассчитайте:
Ø Индивидуальные и общий индекс цен;
Ø Индивидуальные и общий индексы физического объема товарооборота;
Ø Общий индекс товарооборота;
Ø Экономию или перерасход денежных средств населения в результате изменения цен на товары в отчетном периоде по сравнению с базисным
Исх. данные:
| Вид товара | БАЗИСНЫЙ ПЕРИОД ("0") | ОТЧЕТНЫЙ ПЕРИОД ("1") | ||
| Цена за 1 кг, тыс.руб | Продано, тонн | Цена за 1 кг, тыс.руб | Продано, тонн | |
| А | 4,50 | 4,90 | ||
| Б | 2,00 | 2,10 | ||
| В | 1,08 | 1,00 |
Решение:
Индекс – это показатель сравнения двух состояний одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов); включает 2 вида:
ü Отчетные, оцениваемые данные ("1")
ü Базисные, используемые в качестве базы сравнения ("0")
1) Найдем индивидуальные индексы по формулам:
 |




(где: р, q – цена, объем соответственно; р1, р0 - цена отчетного, базисного периодов соответственно; q1, q2 - объем отчетного, базисного периодов соответственно)
· для величины  (цены) по каждому виду товара
(цены) по каждому виду товара
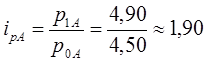


· для величины q (объема) по каждому виду товаров:

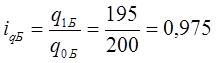

2) Найдем общие индексы по формулам:





представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара.




3) Общий индекс товарооборота равен: 

4) Найдем абсолютное изменение показателя (экономии или перерасхода):


получаем: 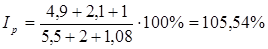
Вывод: наблюдается перерасход денежных средств населения в результате изменения цен на товары в отчетном периоде по сравнению с базисным, в среднем на 5,54%.
Задание 5.
Определить, как изменяться цены на товары, если их стоимость в среднем увеличится на 3,2 %, а физический объем реализации в среднем не изменится.
Решение:
Для базисного периода для цен характерен следующий индекс:

Для отчетного периода известно увеличение стоимости на 3,2 %, т.е.:
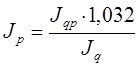
Вывод: из полученного видно, что цены на товары в следствие увеличения их стоимости на 3,2% соответственно возрастут на 3,2%.
 Задание 6.
Задание 6.
Рассчитать коэффициент корреляции по исходным данным своего варианта, используя задание 1.
Решение:
Коэффициент корреляции оценивает тесноту связи между несколькими признаками. В данном случае требуется оценить связь между двумя признаками. Поэтому необходимо рассчитать парный коэффициент корреляции. Воспользуемся следующими формулами:




где:
 - индивидуальные значения факторного и результативного
- индивидуальные значения факторного и результативного
признаков;
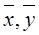 - средние значения признаков;
- средние значения признаков;
 - средняя из произведений индивидуальных значений признаков;
- средняя из произведений индивидуальных значений признаков;
 - средние квадратические отклонения признаков
- средние квадратические отклонения признаков
1) Коэффициент рассчитаем по исходным данным варианта (50 предприятий), которые представлены в табл. 1




2) Расчет средней из произведений проведем в таблице M, заполняя данные о факторном и результативном признаке из таблицы № 1:
| № | Группир. признак | Результат признак | X x Y | № | Группир. признак | Результат признак | XxY | |
| число вагонов, шт/сут | чистая прибыль, млн.руб. | число вагонов, шт/сут | чистая прибыль, млн.руб. | |||||
 60 60
| ||||||||

Расчет коэффициента корреляции проведем по первой из предложенных в начале решения двух формул:

Вывод: т.к. полученный коэффициент корреляции больше значения 0,8, то можно сделать вывод о том, что теснота связи между исследуемыми признаками достаточно тесная.
Задание 7.
По данным своего варианта (см. табл. N) рассчитать индексы сезонности, построить график сезонности и сделать выводы.
Исх. данные:
Табл. N
| Месяц | Годы | Итого за 3 года | В сред-нем за месяц | Индексы сезон-ности, % | ||
| Январь | 90,3 | |||||
| Февраль | 90,6 | |||||
| Март | 110,5 | |||||
| Апрель | 96,1 | |||||
 Май Май
| 95,8 | |||||
| Июнь | 107,4 | |||||
| Июль | 107,8 | |||||
| Август | 107,1 | |||||
| Сентябрь | 93,8 | |||||
| Октябрь | 94,5 | |||||
| Ноябрь | 97,0 | |||||
| Декабрь | 108,0 | |||||
| В среднем | 100,0 |
Сезонными колебаниями называют устойчивые внутригодовые колебания в ряду динамики. Они характеризуются индексами сезонности, совокупность которых на графике образует сезонную волну.
Воспользуемся следующей формулой расчета индексов сезонности:

Vt - фактические (средние) данные по месяцам (среднемесячный
результат, вычисленный за 3 года по одноименным месяцам);
Vo - общая или постоянная средняя (среднемесячный уровень по
36-ти месяцам)









































 Теперь на основании полученных индексов сезонности (ст. 7 табл. N) построим график сезонности:
Теперь на основании полученных индексов сезонности (ст. 7 табл. N) построим график сезонности:
 | |||
 |
Вывод: Сезонность имела три волны подъема количества отправленных вагонов с одной станции:
ü главный – в марте м-це
ü второй (слабее) – в июне-июле м-цах
ü третий (слабее) - в декабре м-це.
Уменьшение наблюдается:
ü в начале года (январь-февраль м-цы)
ü во второй половине весны (апрель-май м-цы)
ü осенью (сентябрь-ноябрь м-цы)
Задание выполнено 10 ноября 1997 года.
_____________________Фролова Е.В.
Литература:
Дружинин Н.К. Математическая статистика в экономике. – М.: Статистика, 1971.
Елисеева И.И. моя профессия – статистик. – М.: Финансы и статистика, 1992.
Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. Чл.-корр. РАН И.И.Елисеевой. – М.: Финансы и статистика, 1996.
Кривенкова Л.Н., Юзбашев М.М. Область существования показателей вариации и ее применение // Вестник статистики. – 1991. - №6. – С.66-70
 Работа над ошибками.
Работа над ошибками.
Задание 4
п.2) Найдем общие индексы цен по формуле Пааше – расчет производится на основе данных о количестве проданных товаров в базисном и отчетном периоде (по каждому j-му товару)




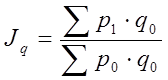

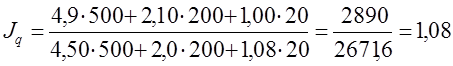
п.3) Найдем общий индекс товарооборота:



Проверка:



 Из проверки видно, что расчет общего индекса товарооборота произведен верно.
Из проверки видно, что расчет общего индекса товарооборота произведен верно.
п.4) Найдем абсолютное изменение показателя (экономия - перерасход):


Получаем:
 Т.к. полученная величина положительно, то мы имеем перерасход средств.
Т.к. полученная величина положительно, то мы имеем перерасход средств.