Метод Гаусса – метод последовательного исключения переменных (впервые описан Гауссом в 1849 г.)
Пусть дана система m линейных уравнений с n неизвестными
, 
или в матричной форме:
.
Здесь А – матрица коэффициентов системы, 
– расширенная матрица системы.
Алгоритм Гаусса. Нахождение множества решений системы линейных уравнений основывается на том, что от заданной системы с помощью элементарных преобразований переходят к системе 
, которая решается проще, чем исходная система, и эквивалентна (равносильна) заданной[1],
Алгоритм Гаусса состоит в том, чтобы получить расширенную матрицу системы 
трапециевидной формы:
= 
(4).
Переход от исходной системы к эквивалентной ей системе с расширенной матрицей (4) называют прямым ходом метода Гаусса.
В зависимости от вида матрицы (4) возможны следующие случаи:
1. Если среди чисел 
, …, 
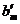есть числа, отличные от нуля, то система несовместна.
2. Если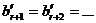 
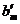= =0, то:
а) при r=n исходная система равносильна системе (которую называют укороченной или треугольной системой)
. (5)
Система (5) (следовательно, и эквивалентная ей исходная система) имеет единственное решение, которое находится по формулам:
(6)
(и т.д. – 
находится из первого уравнения системы).
б) При r<n система исходная система равносильна системе
. (7)
Система (7) имеет бесчисленное множество решений. Назовем неизвестные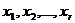 
, (входящие в левую часть системы (7) или в базисный минор) базисными, а остальные неизвестные 
– свободными.
(n–r) свободных переменных можно выбрать произвольно (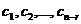
), а базисные переменные можно найти, решая систему (7), например, методом Крамера, которая для каждого набора значений свободных переменных имеет единственное решение:
. (8)
Решение системы в виде вектор-функции от (n–r) свободных неизвестных (формула (8)) называется общим решением системы. [2]
Нахождение значений неизвестных системы (5) или (9) называется обратным ходом метода Гаусса.
Пример 1. Решить методом Гаусса систему
.
Решение:
m=n=4
1. Составим расширенную матрицу системы и приведем её к трапециидальному виду (прямой ход метода Гаусса)
= 
® 
® 
®
® 
® 
®
.
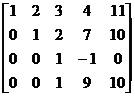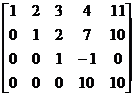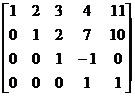2. Определим ранг матрицы.
rang = rang =4.
Ранг матрицы коэффициентов системы равен рангу расширенной матрицы и равен числу неизвестных системы (rang(A) = rang = r=n=4), тогда система имеет единственное решение.
3. Найдем решение системы (обратный ход метода Гаусса):
Запишем укороченную систему
.
Последовательно исключая переменные, найдем
x4 = 1;
x3 = 0+x4 = 1;
x2=10 – 2x3 – 7x4 = 1;
x1 = 11 – 2x2 – 3x3 – 4x4 = 2.
Ответ. 
.
Литература по теме:
а) основная
1. Кремер Н.Ш. Высшая математика для экономического бакалавриата: учебник и практикум. М.: Юрайт, 2014. – 909 с. (ЭБС ЮРАЙТ. – https://www.biblio-online.ru/viewer/EDF405ED-E895-42DE-9744-ED48C83187DC#/).
б) дополнительная
2. Красс М.С. Математика в экономике. Базовый курс. М.: Юрайт, 2015. – 471 с. (ЭБС ЮРАЙТ. – https://www.biblio-online.ru/viewer/8BD2AC05-D7E3-4B22-844C-3DC3D6F52A1B#/).
*Убедиться в правильности уравнения (4) можно, перемножив матрицы А и Х.
[1] Две системы линейных уравнений называются равносильными, если они имеют одинаковые множества решений.
[2] Так как свободные переменные могут принимать любые значения, то общее решение (3.17) описывает бесчисленное множество решений системы.