Векторное произведение
Векторным произведением вектора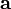 
на вектор 
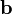в пространстве 
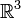называется вектор 
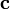, удовлетворяющий следующим требованиям:
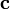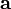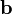- длина вектора равна произведению длин векторов и на синус угла
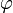; между ними
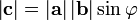
- вектор 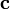ортогонален каждому из векторов 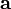и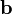
- вектор 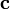направлен так, что тройка векторов
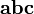является правой. - в случае пространства
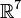требуется ассоциативность тройки векторов 
.
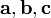Обозначение:
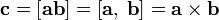
Уравнение прямой на плоскости
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
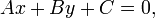
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A, B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.
При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:
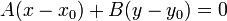
Каноническое уравнение
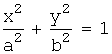- эллипс, Если а>b, то фокусы находятся на оси ОХ на расстоянии 
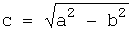от центра эллипса О.
Если а<b, то фокусы находятся на оси ОY и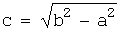 
, 
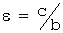. Директрисы
С эллипсом связаны две прямые, называемые директрисами. Их уравнения:
x = a/e; x = -a/e
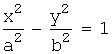- гипербола,
Параметр а называется вещественной полуосью, b – мнимой полуосью. Число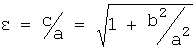 
, (
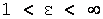)-называется эксцентриситетом гиперболы.
Гипербола, заданная каноническим уравнением: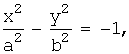 
(или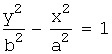 
), этом случае параметр b называется вещественной полуосью, a – мнимой полуосью. Эксцентриситет вычисляется по формуле: 
, ().
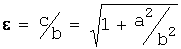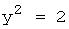px - парабола.
Если р>0, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если р<0 – в отрицательную сторону.
Эллипс
Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F 1 и F 2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
| F 1 M | + | F 2 M | = 2 a, причем | F 1 F 2 | < 2 a.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Каноническое уравнение эллипса. Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
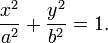
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.
Если а>b, то фокусы находятся на оси ОХ на расстоянии 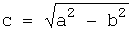от центра эллипса О.
Если а<b, то фокусы находятся на оси ОY и , .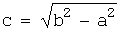
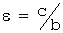Мнимый эллипс
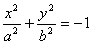- уравнение "мнимого” эллипса.
Тройки векторов
Три вектора называются упорядоченной тройкой(или просто тройкой),если указано, какой из этих векторов является первым, какой вторым и какой третьим. При записи тройки векторов мы всегда будем располагать эти вектора в порядке их исследования. Так,запись bac означает, что первым элементов тройки является вектор b, вторым- вектор а и третьим- вектор с. Всего из трёх векторов можно составить следующие шесть троек: abc bca cab -левые тройки; bac acb acb –левые.
Параметры переменных
Перемножение матриц
Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц. Основной метод перемножения строка на столбец.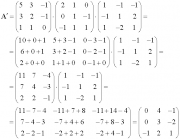 
Метод Гаусса
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Пример
Покажем, как методом Гаусса можно решить следующую систему:
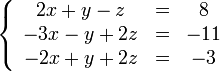
Обнулим коэффициенты при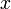 
во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на 
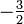и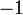 
, соответственно:
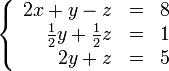
Теперь обнулим коэффициент при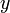 
в третьей строке, вычтя из неё вторую строку, умноженную на 
:
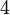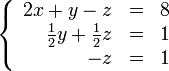
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
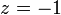из третьего;
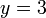из второго, подставив полученное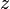 
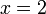из первого, подставив полученные 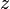и .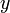
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
точка пересечения прямой в плоскости
Задача 13. Найти точку пересечения прямой и плоскости.
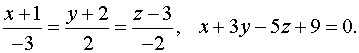
Запишем параметрические уравнения прямой.
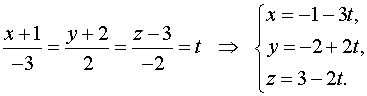
Подставляем в уравнение плоскости:
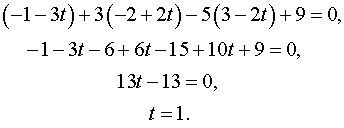
Откуда координаты точки пересечения прямой и плоскости будут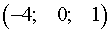 
.