В разделе ВМ. МА – 3 была сформулирована теорема о том, что монотонная ограниченная последовательность имеет предел (п. 3.12).
Применим эту теорему к доказательству существования важного предела, который часто называется вторым замечательным пределом.
Второй замечательный предел (5.16).
Функция 
имеет предел при п ® ¥ и он равен е, то есть 
.
5.16. Второй замечательный предел (адрес файла Блок 4 ___).
Функция  имеет предел при п ® ¥ и он равен е, то есть  .
Вернитесь к тексту
|
Доказательство. ПО формуле бинома Ньютона имеем
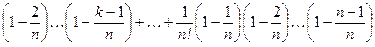
С увеличением п каждое слагаемое (кроме первых двух), стоящее на фиксированном k -ом месте, увеличивается. Действительно,
ставится больше с ростом п. Кроме того, при возрастании п добавляются новые положительные слагаемые. Следовательно, уп – возрастающая функция. Но она ограничена. Действительно, заменив во всех членах правильные дроби, стоящие в скобках, единицами, мы получим:
Мы еще больше увеличим правую часть, если произведем такие замены
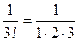на 
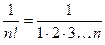на 
…………………………………………………
на 
Следовательно,
.
Но в скобках записана сумма бесконечно убывающей геометрической прогрессии, которая равна 2, то
уп < 3.
Следовательно, данная возрастающая последовательность ограничена сверху, а значит, на основании выше упомянутой теоремы имеет предел, которой заключен между 2 и 3
2 £ уп < 3. Этот предел называется числом е, то есть
.
Число е иррациональное и поэтому не может быть точно выражено какой-нибудь конечной дробью. Приближенно оно равно
е » 2,718281828459045¼
Логарифм числа по основанию е называется натуральным логарифмом и обозначают его ln x.
Покажем, что
х Î (0; +¥).
Для каждого х Î (0; +¥) существует натуральное число п такое, что п < п + 1. Тогда
.
Прибавим единицу ко всем членам неравенства
,
тогда
.
Но
.
Значит
.
Выполнив замену 
, где t ® 0, получим
.
Обращаем Ваше внимание на тот факт, что второй замечательной предел раскрывает неопределенность вида (1¥).
Пример 7. Найти
.
Решение. При х ® ¥ выражение в скобках стремится к единице, так как 2/3 х – бесконечно малая величина и ее предел равен нулю, а показатель стремится к бесконечности, то есть имеем неопределенность вида (1¥). Число е мы получим в том случае, если показатель будет обратным по отношению ко второму слагаемому, то есть 3 х /2.
.
Пример 8. Найти
.
Решение. При х ® ¥ дробь
стремится к единице, а показатель к бесконечности, то есть имеем неопределенность вида (1¥). Преобразуем выражение в скобках
Тогда
.
Тогда второе слагаемое
стремится к нулю при х ® ¥. Далее получаем
.
Пример 9. Найти
.
Решение. При х ® 0 второе слагаемое стремится к нулю, а показатель
стремится к бесконечности. Имеем неопределенность вида (1¥). Тогда
.
Критерии усвоения.
После изучения и анализа содержания темы Вы должны понимать следующее:
- определение предела функции в точке «на языке последовательностей» и «на e - d языке»;
- определение бесконечно большого аргумента;
- определение предела функции при х ® ¥ «на языке последовательностей» и «на e - d языке»;
- определение бесконечно большой и бесконечно малой величин, их связь;
- что такое ограниченная функция в данном интервале и при х ® х 0;
- теорему о функции, имеющей предел;
- теоремы о пределах;
- первый замечательный предел;
- второй замечательный предел.
В результате изучения данной темы Вы должны знать:
- определения предела функции непрерывного аргумента в точке и при х ® ¥;
- как раскрываются неопределенности вида 
, 
;
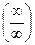- случаи применения первого замечательного предела;
- случаи применения второго замечательного предела.
Ваши знания должны обеспечивать следующие умения:
- находить предел функции при х ® х 0 и х ® ¥;
- раскрывать неопределенности вида 
, 
;
- раскрывать неопределенность вида ; применяя первый замечательный предел;
- раскрывать неопределенность вида 1¥, применяя второй замечательный предел.
5.4. Выход темы в другие разделы курса «Высшая математика» и дисциплины:
- определенный интеграл;
- ряды;
- физика.