Теорема Пифагора
Прямоугольный треугольник — треугольник, в котором один из углов прямой (то есть равен 90°). Сторона, противолежащая прямому углу, называется гипотенузой. Стороны, образующие прямой угол, называются катетами (см. рис.).

Для любого прямоугольного треугольника справедлива теорема Пифагора:

Гипотенузу можно найти по формуле:
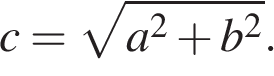
Катет можно найти по формуле:
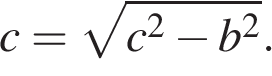
2.2 Как найти  и
и  из прямоугольного треугольника?
из прямоугольного треугольника?
Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c. Обозначим через α угол, лежащий напротив катета a (см. рис.).

Тогда, катет a — противолежащий катет для угла α (лежит напротив угла); катет b — прилежащий катет (непосредственно образует угол).
Синус угла α — отношение противолежащего катета к гипотенузе:

Косинус угла α — отношение прилежащего катета к гипотенузе:
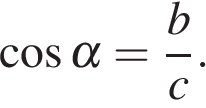
Тангенсом угла α — отношение противолежащего катета к прилежащему:
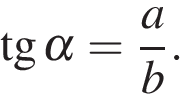
Как найти проекции вектора, если известен его модуль и направление?
1) Опускаем перпендикуляры на ось Ox и ось Oy;

2) Проекции равны:

3) Правило знаков.
Пусть даны вектор  и ось Ox. Из начала и конца вектора
и ось Ox. Из начала и конца вектора  опустим перпендикуляры на ось Ox. Пусть A и B — основания этих перпендикуляров (см. рис.).
опустим перпендикуляры на ось Ox. Пусть A и B — основания этих перпендикуляров (см. рис.).

Проекция 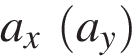 вектора
вектора  на ось Ox (Oy) равна длине отрезка AB, взятой со знаком плюс, если угол φ между вектором
на ось Ox (Oy) равна длине отрезка AB, взятой со знаком плюс, если угол φ между вектором  и осью Ox (Oy) является острым, и взятой соответственно со знаком минус, если φ тупой (или развернутый). Если угол φ прямой, то
и осью Ox (Oy) является острым, и взятой соответственно со знаком минус, если φ тупой (или развернутый). Если угол φ прямой, то 

То есть:

Получаем:

Как найти проекции вектора, если известны координаты начала и конца вектора?

Пусть  и
и  ) — координаты начала и конца вектора <math\vec{a}<math="">соответственно. Тогда проекции</math\vec{a}<>
) — координаты начала и конца вектора <math\vec{a}<math="">соответственно. Тогда проекции</math\vec{a}<>

Как найти модуль вектора, если известны его проекции на оси?
Если известны проекции вектора  и
и 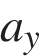 на оси координат, то модуль вектора легко найти по формуле:
на оси координат, то модуль вектора легко найти по формуле:

Как найти модуль вектора, если известны координаты конца и начала вектора?
Пусть  и
и  — координаты начала и конца вектора
— координаты начала и конца вектора  соответственно. Тогда модуль вектора находится по формуле:
соответственно. Тогда модуль вектора находится по формуле:

Теорема косинусов.
Для треугольника со сторонами a, b и c, углом α справедлива теорема:


Как сложить вектора, направленные вдоль одной прямой?
Пусть даны вектора  и
и  имеющие одинаковое направление. Для нахождения вектора
имеющие одинаковое направление. Для нахождения вектора 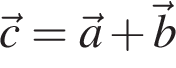 помещаем начало вектора
помещаем начало вектора  в конец вектора
в конец вектора  и соединяем начало вектора
и соединяем начало вектора  с концом вектора
с концом вектора  (см. рис.).
(см. рис.).

Из рисунка видно, что модуль вектора 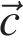 равен:
равен:

Как вычитать вектора, направленные вдоль одной прямой?
Пусть даны вектора  и
и  имеющие одинаковое направление. Для нахождения вектора
имеющие одинаковое направление. Для нахождения вектора 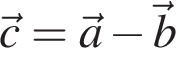 помещаем начало вектора
помещаем начало вектора  в конец вектора
в конец вектора  и соединяем начало вектора
и соединяем начало вектора  с концом вектора
с концом вектора  (см. рис.). Вектор
(см. рис.). Вектор  — это вектор, длина которого равна длине вектора
— это вектор, длина которого равна длине вектора  , но имеет противоположное направление.
, но имеет противоположное направление.

Из рисунка видно, что модуль вектора  равен:
равен:

Как сложить вектора, направленные под прямым углом друг к другу?
Пусть даны вектора  и
и  имеющие одинаковое направление. Для нахождения вектора
имеющие одинаковое направление. Для нахождения вектора 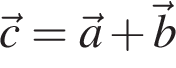 помещаем начало вектора
помещаем начало вектора  в конец вектора
в конец вектора  и соединяем начало вектора
и соединяем начало вектора  с концом вектора
с концом вектора  (см. рис.).
(см. рис.).

Из рисунка видно, что модуль вектора  равен:
равен:
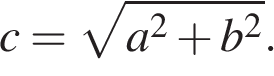
Как вычитать вектора, направленные под прямым углом друг к другу?
Пусть даны вектора  и
и  имеющие одинаковое направление. Для нахождения вектора
имеющие одинаковое направление. Для нахождения вектора 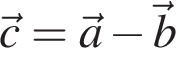 помещаем начало вектора
помещаем начало вектора  в конец вектора
в конец вектора  и соединяем начало вектора
и соединяем начало вектора  с концом вектора
с концом вектора  (см. рис.). Вектор
(см. рис.). Вектор  — это вектор, длина которого равна длине вектора
— это вектор, длина которого равна длине вектора  но имеет противоположное направление.
но имеет противоположное направление.

Из рисунка видно, что модуль вектора 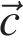 равен:
равен:
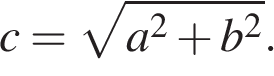
2.12 Как сложить вектора, направленные под углом α друг к другу?
Пусть даны вектора  и
и  , имеющие одинаковое направление. Для нахождения вектора
, имеющие одинаковое направление. Для нахождения вектора 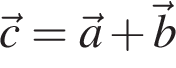 помещаем начало вектора
помещаем начало вектора  в конец вектора
в конец вектора  и соединяем начало вектора
и соединяем начало вектора  с концом вектора
с концом вектора  (см. рис.).
(см. рис.).

По теореме косинусов, получаем:
