Содержание
1. Ситуационная (практическая) задача №1. 3
2. Ситуационная (практическая) задача № 2. 4
Тестовая часть. 6
Список использованных источников. 14
Ситуационная (практическая) задача № 1
Написать три первых члена степенного ряда по заданному общему члену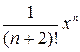 
; найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
Решение задачи
Запишем первые три члена ряда:
;
;
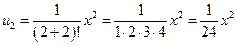Определим радиус сходимости ряда:
, Þ ряд сходится при
xÎ(-¥;+¥), т.е. при всех значениях x.
Ситуационная (практическая) задача № 2
Найти общее решение дифференциального уравнения
и частное решение, удовлетворяющее начальному условию
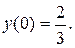
Решение задачи
Пусть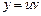 
, тогда 
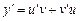. Подставим эти выражения в уравнение:
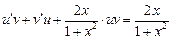
Пусть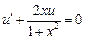 
, тогда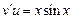 
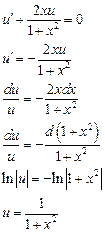
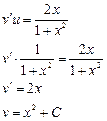
Тогда 
Найдем решение, удовлетворяющее начальным условиям. Т.к. по условию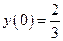 
, то:
Таким образом, частное решение будет: 
Тестовая часть
Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.
1. Применяя таблицу интегралов и метод замены переменных, найти неопределённый интеграл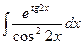 
А.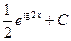 
Б. 
В.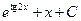 
Г.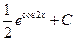 
Решение:
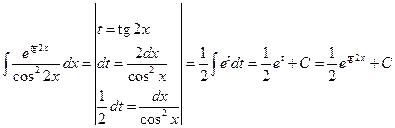
Ответ: А.
2.Применяя метод интегрирования по частям, найти неопределённый интеграл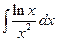 
А. 
Б.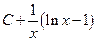 
В.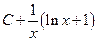 
Г. 
Решение:
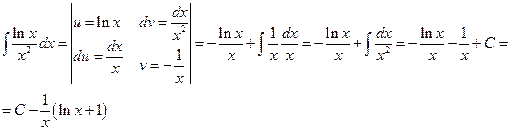
Ответ: А.
3. Применяя метод интегрирования рациональных алгебраических функций, найти неопределённый интеграл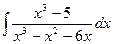 
А.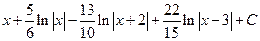 
Б. 
В.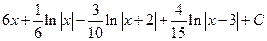 
Г.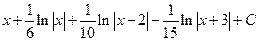 
Решение:
Выделим целую часть
x3-5 x3-x2-6x
x3-x2-6x 1
x2+6x-5
Разложим дробь на простые слагаемые. Для этого сначала разложим знаменатель на множители
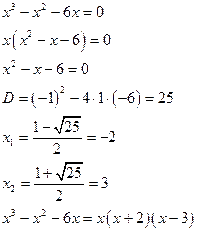
Тогда
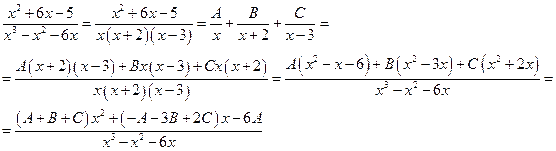
Имеем систему уравнений
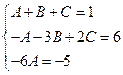
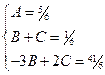
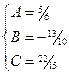
Тогда
Ответ: А.
4. Вычислить площадь фигуры, ограниченной графиками функций 
.
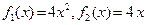А. 3/2
Б. 2/3
В. 4/3
Г. 9/2
Решение:
Построим графики функций
f1(x)=4x2 – парабола.
Вершина параболы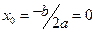 
y0=4×02=0
f2(x)=4x – прямая.
Построим графики функций и определим фигуру
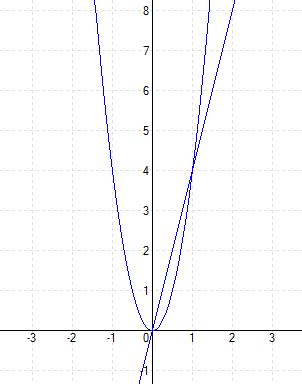
Найдем пределы интегрирования
4x2=4x
4x2-4x=0
4х(х-1)=0
x1=0 x2=1
Для отыскания искомой площади воспользуемся формулой
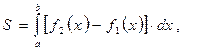
где функции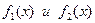 
ограничивают фигуру соответственно снизу и сверху, то есть 
при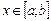 
.
В нашей задаче f2(x)= 4x, f1(x)=4x2,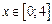 
Вычислим площадь фигуры
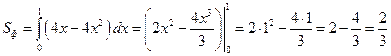
Ответ: Б.
5. Вычислить 
А 
Б.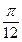 
В. 
Г.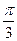 
Решение:
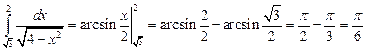
Ответ: А.
6. Выберите расходящийся ряд
А.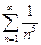 
Б. 
В.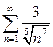 
Г. 
Решение:
Ряд будет расходиться, если показатель степени n в знаменателе для общего члена ряда будет меньше 1.
Ответ: Г.
7. Выберите абсолютно сходящийся ряд
А. 
Б.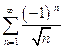 
В.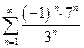 
Г.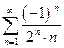 
Решение:
Для рядов А и В не выполняется необходимый признак сходимости ряда, поэтому абсолютной сходимости для них нет. Рассмотрим второй и четвертый ряды. Показатель степени n в знаменателе для общего члена второго ряда равен p=1/2, поэтому для этого ряда также нет абсолютной сходимости. Проверим четвертый ряд на абсолютную сходимость по признаку Даламбера:
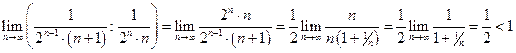
т.е. по признаку Даламбера ряд сходится.
Ответ: Г.
8. В точке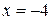 
ряд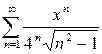 
А. расходится
Б. сходится абсолютно
В. сходится условно
Г. может как сходиться, так и расходиться
Решение:
Подставим x=-4. Получим ряд:
Проверим ряд на абсолютную сходимость. Т.к.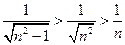 
и гармонический ряд расходится, то первому признаку сравнения также расходится и исходный ряд, Þ абсолютной сходимости нет. Т.к. ряд знакопеременный и 
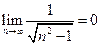, то ряд сходится условно.
Ответ: В.
9. При каком значении параметра С функция 
является решением уравнения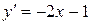 
А.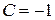 
Б.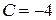 
В.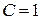 
Г.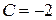 
Решение:
Найдем производную функции: 
. Чтобы она являлась решением уравнения 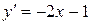, параметр C должен быть равен -1.
Ответ: А.
10. Найти общее решение уравнения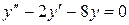 
А.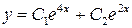 
Б.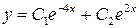 
В.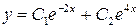 
Г.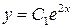 
Решение:
Составляем характеристическое уравнение:
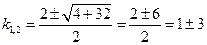
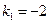
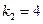
Тогда общее решение запишется в виде:
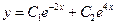
Ответ: В.
Список использованных источников
1. Высшая математика для экономистов. Под редакцией Кремера Н.Ш.- М.: ЮНИТИ, 2009.
2. Кудрявцев Л.Д. Курс математического анализа. Т.1, 2. – М.: Изд-во «Дрофа», 2003.
3. Шипачев В.С. Высшая математика. М.: Высшая школа, - 2007.