ЗАДАЧИ К ОБЩЕМУ ЗАЧЕТУ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ, I СЕМЕСТР.
Предел последовательности
- Пользуясь определением предела последовательности, докажите, что: а)
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. - Докажите, что:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 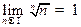 ; д)
; д)  .
.
- Докажите, что последовательности являются бесконечно большими:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
- Докажите, что последовательность
 неограниченная.
неограниченная. - Докажите, что последовательность
 не является бесконечно большой.
не является бесконечно большой. - Докажите сходимость последовательности
 и найдите ее предел, если она определяется рекуррентным соотношением:
и найдите ее предел, если она определяется рекуррентным соотношением:
а)  - произвольное положительное число,
- произвольное положительное число,  . б)
. б)  .
.
- Найдите все предельные точки последовательностей
 , а также
, а также  :
:
а)  ; б)
; б)  ; в)
; в)  .
.
- Исследуйте сходимость последовательности
 в зависимости от параметра α.
в зависимости от параметра α. - Найдите: а)
 ; б)
; б)  ; в)
; в) 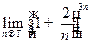 ; г)
; г)  ; д)
; д)  .
.
Предел и непрерывность функции.
- Пусть
 ,
,  ,
,  ,
,  . Докажите, что: а)
. Докажите, что: а)  при
при  ; б)
; б)  при
при  ; в)
; в)  при
при  .
.
11. Найдите: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
12. Найдите: а)  ; б)
; б) 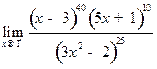 ; в)
; в)  ; г)
; г) 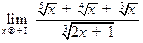 ; д)
; д)  .
.
- Докажите, что не существует: а)
 ; б)
; б)  ; в)
; в)  ; г)
; г) 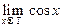 ; д)
; д)  ; е)
; е) 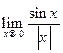 .
. - Докажите, что функция Дирихле
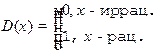 не имеет предела ни в одной точке.
не имеет предела ни в одной точке. - Найдите: а)
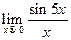 ; б)
; б)  ; в)
; в)  .
. - Докажите, что: а)
 б)
б)  .
. - Укажите все значения
 , для которых верно равенство
, для которых верно равенство  при
при  :
:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е) 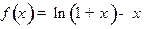 ; ж)
; ж)  .
.
- Пользуясь свойствами символа
 , укажите все значения
, укажите все значения  , для которых верно равенство
, для которых верно равенство  :
:
а)  при
при  ;
;
б)  при
при  ;
;
в)  при
при  ;
;
г)  при
при  ;
;
д)  при
при  .
.
- Укажите все значения
 , при которых верно равенство
, при которых верно равенство  при
при  :
:
а) 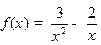 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ; и)
; и)  .
.
20. Напишите формулу Тейлора с центром разложения  и остаточным членом
и остаточным членом 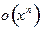 для указанных функций и указанных
для указанных функций и указанных  : а)
: а)  ,
,  ; б)
; б)  ,
,  ; в)
; в) 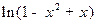 ,
,  ; г)
; г)  ,
,  ; д)
; д)  ,
,  ; е)
; е)  ,
,  .
.
21. Найдите: а) 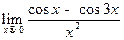 ; б)
; б)  ; в)
; в)  ;
;
22. Найдите: г)  ; д)
; д)  ;
;
е)  ; ж)
; ж)  .
.
23. Найдите: а)  ; б)
; б)  ; в)
; в)  .
.
24. Найдите: а)  ; б)
; б)  ; в)
; в)  .
.
25. Найдите: а)  ; б)
; б)  ; в)
; в)  .
.
26. Найдите: а)  ; б)
; б)  ; в)
; в)  .
.
- Найдите точки разрыва функций и укажите их тип: а)
 ; б)
; б)  ; в)
; в)  ; г)
; г) 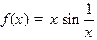 ; д)
; д)  ; е)
; е)  .
.
Дифференцирование
28. Пользуясь определением производной, найдите производную функции  в точке
в точке  :
:
а)  ,
, 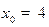 ; б)
; б)  ,
,  ; в)
; в)  ,
,  ,
,  ,
,  .
.
29. Найдите левую и правую производные функций:
а)  в точке
в точке  ; б)
; б)  в точке
в точке  ;
;
в)  в точке
в точке  ; г)
; г)  в точке
в точке  ;
;
д)  в точке
в точке  .
.
30. Найдите производную и дифференциал функции  :
:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ;
;
з)  ; и)
; и)  ; к)
; к) 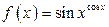 .
.
31. Найдите производную функции  в точке
в точке  . Найдите значение дифференциала функции
. Найдите значение дифференциала функции  в точке
в точке  для указанного значения
для указанного значения  :
:
а)  ; б)
; б)  .
.
32. Найдите первую и вторую производные функции  в точке
в точке  . Найдите значения первого и второго дифференциалов функции
. Найдите значения первого и второго дифференциалов функции  в точке
в точке  для указанного значения
для указанного значения  :
:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
33. Пусть  причем функция
причем функция  имеет левую производную в точке
имеет левую производную в точке 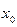 . При каком выборе коэффициентов
. При каком выборе коэффициентов  и
и  функция
функция  будет: а) непрерывной в точке
будет: а) непрерывной в точке  ? б) дифференцируемой в точке
? б) дифференцируемой в точке  ?
?
34. Пусть  При каком выборе коэффициентов
При каком выборе коэффициентов  и
и  функция
функция  будет: а) непрерывной; б) дифференцируемой на промежутке
будет: а) непрерывной; б) дифференцируемой на промежутке  ?
?
35. Заменяя функцию (подберите ее самостоятельно) многочленом Тейлора  , найдите приближенное значение числа
, найдите приближенное значение числа 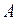 без калькулятора: а)
без калькулятора: а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  .
.
36. Напишите уравнение касательной к графику функции  , заданной параметрически уравнениями
, заданной параметрически уравнениями  ,
,  , при: а)
, при: а) 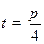 ; б)
; б)  .
.
37. Напишите уравнение касательной к графику функции  , заданной параметрически уравнениями
, заданной параметрически уравнениями  ,
,  , при: а)
, при: а) 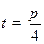 ; б)
; б)  .
.
38. Найдите дифференциал n -го порядка функции  : а)
: а)  ; б)
; б) 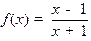 ; в)
; в)  ; г)
; г)  .
.
39. Найдите дифференциал  –го порядка функции
–го порядка функции  для указанного
для указанного  :
:
а)  ,
,  ; б)
; б)  ,
, 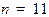 ; в)
; в)  .
.
40. Найдите точку c в формуле конечных приращений Лагранжа  для функции
для функции  на сегменте
на сегменте  .
.
41. Используя правило Лопиталя, найдите: а)  ; б)
; б)  ; в)
; в) 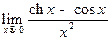 ; г)
; г) 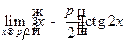 ; д)
; д)  .
.
42. Напишите формулу Тейлора с многочленом Тейлора порядка  и остаточным членом в форме Пеано с центром разложения в точке
и остаточным членом в форме Пеано с центром разложения в точке 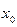 для функций:
для функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
43. Разложите по формуле Маклорена до члена указанного порядка n включительно следующие функции: а)  ; б)
; б) 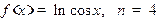 ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
44. Найдите значение многочлена Тейлора  функции
функции  для указанных значений
для указанных значений  ,
,  и
и  :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
45. Напишите выражение остаточного члена  в форме Лагранжа формулы Тейлора для функции
в форме Лагранжа формулы Тейлора для функции  для указанных значений
для указанных значений 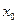 ,
,  и
и  :
:
а)  ;
;
б)  ;
;
в)  .
.
46. Найдите: а) 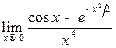 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
Исследование поведения функций и построение графиков
47. Найдите промежутки возрастания и убывания функции  , точки локального экстремума, промежутки сохранения направления выпуклости, точки перегиба. Нарисуйте эскиз графика функции: а)
, точки локального экстремума, промежутки сохранения направления выпуклости, точки перегиба. Нарисуйте эскиз графика функции: а)  ; б)
; б) 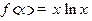 ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.
48. Найдите промежутки возрастания и убывания функции  , точки локального экстремума. Найдите наклонные асимптоты графика функции. Нарисуйте эскиз графика функции: а)
, точки локального экстремума. Найдите наклонные асимптоты графика функции. Нарисуйте эскиз графика функции: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; e)
; e)  ; ж)
; ж)  ; з)
; з)  ; и)
; и)  .
.
Интегрирование.
49. Найдите: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
50. Найдите: а) 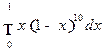 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е) 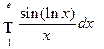 ; ж)
; ж)  ; з)
; з)  ; и)
; и)  .
.
51. Найдите: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж) 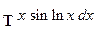 .
.
52. Найдите: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
53. Найдите: а)  ; б)
; б)  .
.
54. Найдите: а)  ; б)
; б)  ; в)
; в) 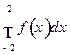 , если
, если 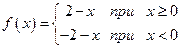 .
.
55. Найдите: а)  ; б)
; б)  ; в)
; в)  .
.
56. Найдите: а)  ; б)
; б)  .
.
57. Найдите: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
58. Найдите: а)  ; б)
; б)  .
.
59. Найдите: а)  , б)
, б)  ;
;
60. Найдите: а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
61. Найдите: а)  ; б)
; б) 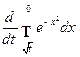 ; в)
; в)  ; г)
; г) 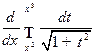 ; д)
; д)  .
.