Общие подходы к формированию критериев оценивания
Требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Не следует требовать от учащихся слишком подробных комментариев (например, описания алгоритмов). Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, следует рассматривать как решение без недочетов.
Если решение ученика удовлетворяет этим требованиям, то ему выставляется полный балл, которым оценивается это задание: № 21 и 24 – 2 балла, № 22 и 25 – 3 балла, № 23 и 26 – 4 балла. Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного.
В критериях оценивания по каждому конкретному заданию второй части экзаменационной работы эти общие позиции конкретизируются и пополняются с учетом содержания задания. Критерии разработаны применительно к одному из возможных решений, а именно, к тому, которое описано в рекомендациях. При наличии в работах учащихся других решений критерии вырабатываются предметной комиссией с учетом описанного общего подхода. Решения учащихся могут содержать недочеты, не отраженные в критериях, но которые, тем не менее, позволяют оценить результат выполнения задания положительно (со снятием одного балла). В подобных случаях решение о том, как квалифицировать такой недочет, принимает предметная комиссия.
Критерии проверки и оценивания выполнения заданий с развернутым ответом
Задание 21
1. Разложите на множители:  .
.
Ответ:  .
.
Решение. 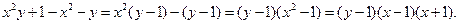
| Баллы | Критерии оценки выполнения задания |
| Правильно и до конца (получено три множителя) выполнено разложение на множители. | |
| Ход решения верный, не содержит ошибок, но разложение на множители не доведено до конца (выражение представлено в виде произведения двух множителей). | |
| Другие случаи, не соответствующие указанным критериям. |
Комментарий. Ошибка в знаках при группировке слагаемых считается существенной, при ее наличии решение не засчитывается.
Примеры выполнения заданий учащимися
Пример 1.
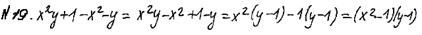
За решение выставляется 1 балл, так как оно не содержит ошибок, но разложение на множители не доведено до конца.
Пример 2.

За решение выставляется 0 баллов; допущена ошибка в знаках при группировке слагаемых (см. комментарий к критериям).
2. Сократите дробь  .
.
Ответ:  .
.
Решение. Корни квадратного трехчлена  : х 1 = 1, х 2 =
: х 1 = 1, х 2 = 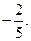 Имеем
Имеем
 .
.
Замечание. Учащийся может разложить трехчлен на множители каким-либо иным способом. Например:
5 x 2 – 3 x – 2 = (3 x 2 – 3 x) + (2 x 2 – 2) = 3 x (x – 1) + 2(x 2 – 1) = (x – 1)(5 x + 2).
| Баллы | Критерии оценки выполнения задания |
| Правильно выполнено разложение на множители числителя и знаменателя дроби, получен верный ответ. | |
| Допущена описка или ошибка вычислительного характера при нахождении корней квадратного трехчлена, но разложение его на множители с учетом этой ошибки выполнено верно, решение при этом может оказаться не доведенным до конца. | |
| Другие случаи, не соответствующие указанным критериям |
Комментарий. Учащиеся не обязаны указывать область определения сокращаемой дроби.
Примеры выполнения заданий учащимися
Пример 1.


За решение выставляется 2 балла. Все шаги выполнены верно, получен правильный ответ.
Пример 2.

Сокращение дроби выполнено верно. Но так как при указании ОДЗ допущена ошибка (хотя нахождение области определения дроби в данном случае не требуется), за решение выставляется 1 балл.
Задание 22
1. Решите неравенство 
Ответ: 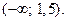 Другая возможная форма ответа:
Другая возможная форма ответа: 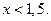
Решение. 1) Определим знак разности  Так как
Так как 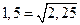 и
и 
то 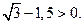
2) Получаем неравенство  Отсюда
Отсюда 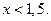
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, оба его шага выполнены, получен верный ответ. | |
| Ход решения верный, правильно выполнен первый шаг, но при решении линейного неравенства допущена вычислительная ошибка или описка. | |
| Другие случаи, не соответствующие указанным критериям. |
Примеры выполнения заданий учащимися
Пример 1.

Допущена ошибка вычислительного характера на последнем шаге решения. Оценка снижается на 1 балл, за решение выставляется 2 балла.
Замечание. Можно не требовать дополнительных пояснений в предъявленной цепочке выкладок, так как, по всей видимости, учащийся знает, что  , и для него очевидно, что
, и для него очевидно, что 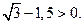
Пример 2

Допущена ошибка принципиального характера в алгоритме решения неравенства. За решение выставляется 0 баллов.
2. Постройте график функции  , где
, где

При каких значениях х функция принимает значения, меньшие 2?
Ответ: график изображен на рисунке 1;  при
при  .
.
| Рис. 1 | 
| |||
| Баллы | Критерии оценки выполнения задания | |||
| Правильно построен график, дан правильный ответ на вопрос. | ||||
| Правильно построен график, но отсутствует ответ на вопрос; ИЛИ при правильно вычисленных координатах точек графика допущена неточность в построении, ответ дан с учетом этой неточности; ИЛИ при записи ответа допущена погрешность, например, вместо круглой скобки поставлена квадратная. | ||||
| Другие случаи, не соответствующие указанным критериям. | ||||
Комментарий.
1. Отсутствие пояснений и письменных вычислений при правильном построении графика и правильном ответе на вопрос не должно служить основанием для снижения балла.
2. Ответ на вопрос задания может быть получен как путем вычислений, так и с опорой на график.
3. Ответ на вопрос может быть записан в любой правильной форме.
Примеры выполнения заданий учащимися
Пример 1.

За решение выставляется 0 баллов. Учащийся должен был выделить каким-либо способом (например, жирно) собственно график заданной функции.
Пример 2.
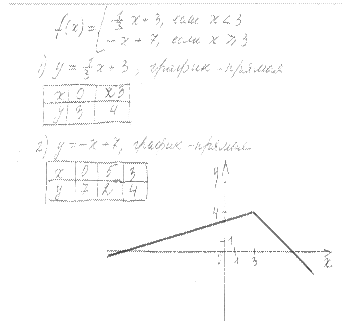
График построен правильно, отсутствует ответ на вопрос. В соответствии с критериями выставляется 2 балла.
3. Найдите область определения выражения  .
.
Ответ: 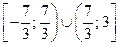 .
.
Решение. Область определения выражения задается условиями 
Решим неравенство  :
:  ; х 1 =
; х 1 =  , х 2 = 3;
, х 2 = 3; 
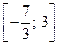 ;
;
Из условия  имеем
имеем  . Отсюда
. Отсюда 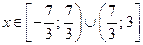 .
.
Замечание. Ответ может быть представлен в форме: 
| Баллы | Критерии оценки выполнения задания |
| Учтены оба условия, задающие область определения данного выражения, все выкладки выполнены верно, получен верный ответ. | |
| Ход решения правильный, решение доведено до конца, но допущена ошибка в символической записи ответа; ИЛИ допущена описка или ошибка вычислительного характера (например, при вычислении корней квадратного трехчлена), и с ее учетом дальнейшие шаги выполнены верно; ИЛИ при определении области определения квадратного корня рассмотрено строгое неравенство. | |
| Другие случаи, не соответствующие указанным критериям. |
Комментарий. Ошибки в алгоритме решения квадратного неравенства, в применении формулы корней квадратного уравнения считаются существенными, и решение при их наличии не засчитывается.
Примеры выполнения заданий учащимися
Пример 1

За решение выставляется 2 балла. Ход рассуждений понятен, он правильный, получен верный ответ. Балл снижен за некорректное пояснение, приведенное в начале решения.
Замечание. Вопросительные знаки поставлены на схеме экспертом; мы в этом рисунке недочетов не видим.
Пример 2.


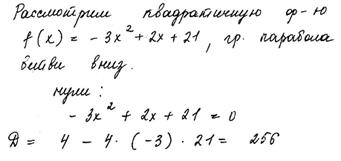



| 
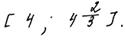
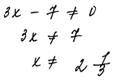


|
За решение выставляется 0 баллов; в нем содержится более одной ошибки, поэтому оно соответствует графе «Другие случаи, не соответствующие указанным критериям». Учащимся, во-первых, допущены две вычислительные ошибки при нахождении корней квадратного трехчлена; во-вторых, решив квадратное неравенство (с учетом найденных корней) и правильно наложив ограничение на знаменатель дроби, учащийся не сумел сделать на основе полученных результатов соответствующий вывод.
4. Найдите сумму всех отрицательных членов арифметической прогрессии
– 8,6; – 8,4; …
Ответ: 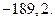
Решение. 1. Найдем разность прогрессии: 
2. Найдем число отрицательных членов прогрессии.
Составим формулу n -го члена:  =
= 
Решим неравенство  получим
получим  Значит,
Значит, 
3.  =
=  .
.
| Баллы | Критерии оценки выполнения задания |
| Ход решения правильный, все его шаги выполнены верно, получен верный ответ. | |
| Ход решения правильный, решение доведено до конца, но допущена одна описка или непринципиальная ошибка вычислительного характера, с ее учетом дальнейшие шаги выполнены верно. | |
| Другие случаи, не соответствующие указанным критериям. |
Комментарий.
1. Учащийся имеет право воспользоваться другой формулой суммы первых n членов арифметической прогрессии.
2. Ошибки в применении формул, в том числе в подстановке числовых значений в формулы, считаются существенными, решение не засчитывается и оценивается 0 баллов.
Примеры выполнения заданий учащимися
Пример 1.


Ход решения верный, но допущена вычислительная ошибка (при нахождении разности арифметической прогрессии), с ее учетом решение доведено до конца. Выставляется 2 балла.
Задание 23
1. Решите систему уравнений 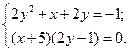
Ответ:  Другие возможные формы записи ответа:
Другие возможные формы записи ответа:  ;
; 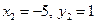 ;
;  ;
;
или 


Решение. На основании условия равенства произведения нулю получим:
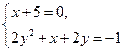 или
или 
Решим первую систему. Из первого уравнения имеем x = –5; подставив это значение
x во второе уравнение, получим уравнение 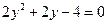 . Его корни: y 1 = –2, y 2 = 1.
. Его корни: y 1 = –2, y 2 = 1.
Получаем два решения системы уравнений: (–5; –2) и (–5; 1).
Решив вторую систему, получим: y = 0,5; x = –2,5. Получаем еще одно решение
системы уравнений: (–2,5; 0,5).
Таким образом, система имеет три решения:  .
.
| Баллы | Критерии оценки выполнения задания |
| Правильно выполнен переход от данной системы к равносильной ей дизъюнкции (совокупности) двух систем, все дальнейшие шаги выполнены верно, получен верный ответ. | |
| Ход решения правильный, решение доведено до конца, найденные значения переменных правильно объединены в пары, но: ИЛИ допущена одна непринципиальная вычислительная ошибка (например, при нахождении корней квадратного уравнения) или описка, с ее учетом все дальнейшие шаги выполнены верно; ИЛИ допущены погрешности логического характера в употреблении символики (если она применяется). | |
| Другие случаи, не соответствующие указанным критериям. |
Комментарий. Ошибки при объединении найденных значений переменных в пары считаются существенными; в этом случае решение не засчитывается. Если имеется более двух вычислительных ошибок или решение не доведено до конца, то оно не засчитывается.
Примеры выполнения заданий учащимися
Пример 1.


|  
|
За решение выставляется 3 балла; допущены ошибки в употреблении символики.
Пример 2.

За решение можно выставить 3 балла: ход решения правильный, и, по сути, верный ответ получен. Но решение содержит логическую ошибку: выполнив проверку (которая в данном случае не является составной частью решения и может служить только цели самоконтроля), учащийся допустил вычислительную ошибку и сделал неправильный вывод о наличии постороннего решения, которого в принципе в данной ситуации быть не может.
Замечание. За нерациональное решение баллы не снимаются. Хотя хотелось бы, чтобы для сильного учащегося наличие уравнения  сразу же служило сигналом к попытке применить условие равенства нулю произведения. Приведенное решение показывает (и это не единичный случай), что не наработаны некоторые стандартные приемы, обязательные для подготовки сильного ученика.
сразу же служило сигналом к попытке применить условие равенства нулю произведения. Приведенное решение показывает (и это не единичный случай), что не наработаны некоторые стандартные приемы, обязательные для подготовки сильного ученика.
2. Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
Ответ: плот пройдет  всего пути.
всего пути.
Решение. Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна 4 х – х = 3 х км/ч, а по течению 4 х + х = 5 х км/ч. Следовательно, скорость катера против течения в 3 раза больше скорости плота, а по течению – в 5 раз больше скорости плота. Если плот до встречи проплыл S км, то катер – в 3 раза больше, т. е. 3 S км. После встречи катер пройдет 3 S км, а плот – в 5 раз меньше, т. е.  км. Всего плот пройдет
км. Всего плот пройдет  . Отношение пройденного плотом пути ко всему пути равно
. Отношение пройденного плотом пути ко всему пути равно 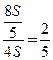 .
.
Другое возможное решение. Пусть скорость течения реки (и плота) х км/ч. Тогда скорость катера против течения равна 4 х – х = 3 х км/ч, а по течению 4 х + х = 5 х км/ч. Скорость сближения катера и плота равна х + 3 х = 4 х км/ч. Встреча произошла через  ч. За это время плот проплыл расстояние, равное
ч. За это время плот проплыл расстояние, равное  , а катер –
, а катер – 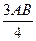 . Обратный путь катер пройдет за
. Обратный путь катер пройдет за 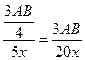 ч. Плот за это время проплывет расстояние, равное
ч. Плот за это время проплывет расстояние, равное  , а всего он проплывет
, а всего он проплывет  .
.
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, все его шаги выполнены, получен верный ответ. | |
| Ход решения верный, все его шаги выполнены, но допущена одна ошибка – в преобразованиях или в вычислениях, с ее учетом дальнейшие шаги выполнены правильно. | |
| Другие случаи, не соответствующие указанным критериям. |
Примеры выполнения заданий учащимися
Пример 1.


Ход решения верный, введены нужные обозначения, приведены пояснения, но допущена вычислительная ошибка, с ее учетом решение доведено до конца. Можно выставить 3 балла.
Пример 2.

При нахождении длины пути, который катер проплыл против течения, учащийся использует собственную скорость катера; решение оценивается 0 баллами.
3. Найдите все значения а, при которых неравенство х2 + (2 а + 4) х + 8 а + 1 ≤ 0 не имеет решений.
Ответ:  ; другая возможная форма ответа:
; другая возможная форма ответа:  (1; 3).
(1; 3).
Решение. График функции у = х 2 + (2 а + 4) х + 8 а + 1 – парабола, ветви которой направлены вверх. Значит, данное неравенство не имеет решений в том и только том случае, если эта парабола целиком расположена в верхней полуплоскости. Отсюда следует, что дискриминант квадратного трехчлена х 2 + (2 а + 4) х + 8 а + 1 должен быть отрицателен.
Имеем  .
.
Решив квадратное неравенство, получаем  .
.
Замечание. Учащийся может воспользоваться формулой дискриминанта 
Другое возможное решение. Найдем ординату вершины параболы у 0 и выясним, при каких значениях а выполняется неравенство у 0 > 0.
| Баллы | Критерии оценки выполнения задания |
| Найден правильный способ решения, все шаги выполнены верно, получен правильный ответ. | |
| Найден правильный способ решения, все шаги выполнены верно, но допущена одна ошибка технического характера (вычислительная или в преобразованиях), при этом решение доведено до конца (ответ может отличаться от правильного). | |
| Другие случаи, не соответствующие указанным критериям. |
Комментарий. Ошибки при составлении дискриминанта квадратного трехчлена или в применении алгоритма решения квадратного неравенства являются существенными, и при их наличии за решение выставляется 0 баллов.
Примеры выполнения заданий учащимися
Пример 1.



Все шаги решения выполнены верно (хотя есть погрешность в терминологии), получен правильный ответ. За решение можно выставить 4 балла.
Пример 2.
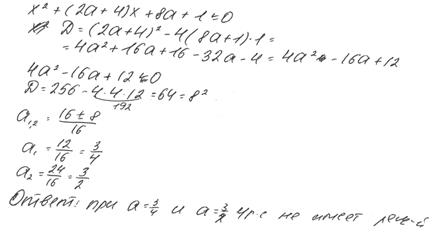
За решение выставляется 0 баллов. Учащийся не владеет приемом решения квадратного неравенства, допускает ошибки в применении формулы корней квадратного уравнения.
4. Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Ответ: 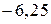 ;
;  ; 6.
; 6.
Решение. Разложим числитель на множители:
 .
.
При  ,
,  исходная функция принимает вид
исходная функция принимает вид  , её график — парабола, из которой выколоты точки
, её график — парабола, из которой выколоты точки  и
и  .
. 
Прямая  имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты
имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты  .
.
Поэтому  ,
,  или
или  .
.
| Баллы | Критерии оценивания выполнения задания |
График построен правильно, верно указаны все значения  , при которых прямая , при которых прямая  имеет с графиком только одну общую точку имеет с графиком только одну общую точку
| |
График построен правильно, указаны не все верные значения 
| |
| Другие случаи, не соответствующие указанным выше критериям |
Примеры выполнения заданий учащимися
Пример 1.

|
За решение выставляется 3 балла. Учащийся верно упростил выражение, указал ОДЗ, верно построил график и выколол обе точки, но не учел, что прямая, параллельная оси абсцисс имеет с параболой одну общую точку, проходя через ее вершину. Один балл снят за потерю соответствующего значения параметра.
Пример 2.

|
За решение выставляется 3 балла. Один балл снят за то, что учащийся не указал еще два решения, соответствующих выколотым точкам параболы.
Пример 3.

|
Задание выполнено верно, за его выполнение выставляется 4 балла.
Задание 24
1. Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите  , если , если  .
Ответ: .
Ответ:  . .
| 
|
Решение.
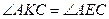 , т.к. опираются на одну дугу окружности; следовательно, , т.к. опираются на одну дугу окружности; следовательно, 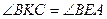 , как смежные с ними. Из четырехугольника , как смежные с ними. Из четырехугольника  : :  . Из . Из 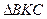 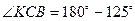  . .
| 
|
| Баллы | Критерии оценивания выполнения заданий |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, все его шаги выполнены правильно, но не даны объяснения или допущена одна вычислительная ошибка | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Примеры выполнения заданий учащимися
Пример 1.

За выполнение задания выставляется 1 балл, т.к. отсутствуют пояснения и ссылки на использованные теоремы.
Пример 2.

За задание выставляется 1 балл, т.к. допущена вычислительная ошибка, которая не носит принципиального характера; задание доведено до конца.
Задание 25
1. В окружности с центром  проведены две хорды проведены две хорды 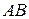 и и  так, что центральные углы так, что центральные углы  и и 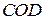 равны. На эти хорды опущены перпендикуляры равны. На эти хорды опущены перпендикуляры  и и  . Докажите, что . Докажите, что  и и  равны. равны.
| 
|
Доказательство. Треугольники  и и 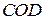 равны по трём сторонам.
Треугольники равны по трём сторонам.
Треугольники  и и 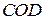 равны по двум сторонам и углу между ними (АО = ВО = СО = DO как радиусы окружности, равны по двум сторонам и углу между ними (АО = ВО = СО = DO как радиусы окружности,  по условию). Следовательно, высоты по условию). Следовательно, высоты  и и  равны как соответственные элементы равных треугольников. равны как соответственные элементы равных треугольников.
| 
|
| Баллы | Критерии оценивания выполнения задания |
| Доказательство верное | |
| Доказательство содержит неточности | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Примеры выполнения заданий учащимися
Пример 1.

|
Учащийся не указывает явно, что OK и OL являются высотами рассматриваемых треугольников, но использует это в неявном виде, переходя к формуле площади треугольника. Это можно не считать неточностью. За выполнение задания выставляется 3 балла.
Замечание. Учащиеся должны указывать соответствующий признак равенства треугольников.
Пример 2.

|
Учащийся не указал соответствующий признак равенства треугольников. За эту неточность снимается 1 балл и выставляется 2 балла.
2. В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK = EN. Докажите, что данный параллелограмм — прямоугольник.
Решение.
Доказательство. 
Треугольники 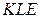 и
и  равны по трём сторонам.
равны по трём сторонам.
Значит, углы 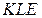 и
и  равны. Так как их сумма равна
равны. Так как их сумма равна 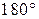 , то углы равны
, то углы равны  . Такой параллелограмм — прямоугольник.
. Такой параллелограмм — прямоугольник.
| Баллы | Критерии оценивания выполнения задания |
| Доказательство верное | |
| Доказательство содержит неточности | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Пример 1.

За задание выставляется 0 балл, т.к. отсутствует доказательство равенства углов  и
и  , что является существенным моментом предложенного доказательства. Комментарий. Учащийся был введен в заблуждение своим рисунком: если бы он изобразил параллелограмм, а не прямоугольник, этого бы не случилось.
, что является существенным моментом предложенного доказательства. Комментарий. Учащийся был введен в заблуждение своим рисунком: если бы он изобразил параллелограмм, а не прямоугольник, этого бы не случилось.
Пример 2.

|

|
Доказательство логично, хорошо структурировано, не содержит пробелов, утверждения аргументированы. За задание выставляется максимальный балл – 3.
Комментарий. 1) Фразу в приведенном доказательстве «видно по рисунку» следует трактовать, как неуклюжее выражение очевидной мысли о том, что заданное в условии задачи условие равенства отрезков EL и EM отмечено на рисунке, в треугольнике ELM стороны EL и EM равны, следовательно, треугольник ELM является равнобедренным.
2) Фразу «его противоположные стороны равны» следует считать опиской, так как далее речь идет об углах параллелограмма.
3) Запись «
 », скорее похожа на шифрограмму, ее, конечно, нельзя признать грамотной, но выраженная таким образом мысль понятна и должна быть засчитана.
», скорее похожа на шифрограмму, ее, конечно, нельзя признать грамотной, но выраженная таким образом мысль понятна и должна быть засчитана.
Задание 26
1. Площадь треугольника  равна 80. Биссектриса
равна 80. Биссектриса  пересекает медиану
пересекает медиану  в точке
в точке 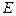 , при этом
, при этом 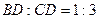 . Найдите площадь четырёхугольника
. Найдите площадь четырёхугольника  .
.
Ответ: 36.
Решение. Пусть  , тогда , тогда  , так как , так как 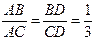 по свойству биссектрисы. Значит, по свойству биссектрисы. Значит,  . .
| 
|
Пусть  — площадь треугольника
— площадь треугольника 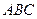 , тогда
, тогда 

Таким образом,  .
.
| Баллы | Критерии оценивания выполнения задания |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка | |
| Другие случаи, не соответствующие указанным выше критериям |
Примеры выполнения заданий учащимися
Пример 1.

На третьем шаге, выражая площадь треугольника  через площадь треугольника
через площадь треугольника  , ученик допустил ошибку, верна следующая запись:
, ученик допустил ошибку, верна следующая запись:  . С учетом этой ошибки решение доведено до конца. За выполнение задания выставляется 3 балла.
. С учетом этой ошибки решение доведено до конца. За выполнение задания выставляется 3 балла.
Пример 2.

Задание выполнено верно, выставляется 4 балла.
2. Стороны  ,
,  ,
,  треугольника
треугольника 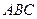 равны
равны 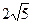 ,
,  и 1 соответственно. Точка
и 1 соответственно. Точка  расположена вне треугольника
расположена вне треугольника 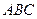 , причем отрезок
, причем отрезок  пересекает отрезок
пересекает отрезок  в точке, отличной от
в точке, отличной от 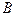 . Известно, что треугольник с вершинами
. Известно, что треугольник с вершинами  ,
, 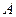 и
и  подобен исходному. Найдите косинус угла
подобен исходному. Найдите косинус угла 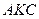 , если
, если  .
.
Ответ: 
Решение: 
Рассмотрим подобные треугольники  и
и  и установим соответствие между их углами.
и установим соответствие между их углами.
 — наибольшая сторона треугольника
— наибольшая сторона треугольника  , а значит,
, а значит,  — наибольший угол треугольника
— наибольший угол треугольника