А.Ф. Карелин
Методическое руководство
По решению задач о кредитном контракте,
основанном на дифференцированной системе платежей
(задача №17 из вариантов ЕГЭ профильного уровня по математике)
Москва
© Карелин А.Ф.
Для школьников, намеревающихся получить высокий балл при сдаче Единого государственного экзамена по математике профильного уровня, важно научиться решать задачу № 17 («Финансовая математика»). Набор типов задач № 17, встречающихся в изданных сборниках тренировочных вариантов по подготовке к ЕГЭ, достаточно разнообразен, и всё же большинство из них приходится на задачи о банковских кредитах, среди которых, в свою очередь, особое место занимают задачи о кредитных контрактах, основанных на так называемой дифференцированной системе платежей.
В отличие от системы аннуитетных платежей, принятой в большинстве привычных для населения потребительских или ипотечных кредитных договоров, когда кредит возвращается равными периодическими платежами, при схеме дифференцированных платежей периодические выплаты осуществляются с таким расчётом, чтобы после каждого платежа остаток долга уменьшался на одну и ту же величину – при этом сами платежи получаются, разумеется, неодинаковыми, составляя некоторую арифметическую прогрессию. Поскольку в стандартных курсах математики для средних общеобразовательных школ не предусмотрено изучение формул, связывающих между собой параметры контракта, основанного на дифференцированной системе платежей, мы сочли необходимым восполнить этот пробел, представив вывод этих формул в общем виде.
Необходимо иметь в виду, что непосредственное применение указанных формул без их вывода при решении задачи № 17 на экзамене, вообще говоря, не гарантирует получения максимальных баллов за данную задачу – именно потому, что формулы не содержатся в готовом виде в школьной программе. Тут многое зависит от позиции проверяющих. Поэтому на всякий случай имеет смысл на экзамене в сокращённом виде повторить представленные здесь выводы формул. Однако, если ученик запомнил сами формулы, но вывести их почему-либо не смог, то, конечно, следует использовать их без вывода – задача с верным ответом и решением, даже оценённым как «неполное», будет зачтена как минимум с частичными баллами.
***
Типичная задача о кредитном контракте с дифференцированной системой платежей выглядит, например, так:
Задача 1. 15-го января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Прежде, чем решать задачу, перечислим все используемые в решении величины с соответствующими обозначениями:
С – сумма кредита (в рублях);
n – срок кредита (в месяцах);
r – процентная ставка по кредиту (в процентах);
платёж за m -ый месяц (в рублях);
– долг перед банком после m -ого платежа (в рублях);
– сумма, выплачиваемая банку за период с k -го по m -ый месяц (в рублях).
Рассмотрим, что будет происходить с нашим кредитом. В приведенном примере 1 февраля будут начислены проценты, и сумма долга увеличится на 3%, составив 2400000*1,03 = 2472000 рублей. А не позднее 14 февраля необходимо внести первый платёж, размер которого надо вычислить, исходя из требования погасить весь долг за два года, причём остаток долга ежемесячного должен уменьшаться на одну и ту же величину. Поэтому лучше всего сначала решить задачу в общем (буквенном) виде, то есть вывести необходимые формулы – а уже потом подставлять в них заданные в конкретной задаче числовые значения.
После первого начисления процентов долг станет равен (1 + 0,01 r) C, а после внесения первого платежа он уменьшится на сумму этого платежа, составив
= (1 + 0,01 r) C – 
, (1)
где 
размер первого платежа, – остаток долга после его внесения.
Поскольку платежи вносятся ежемесячно, очевидно, что последовательность остатков долга будет включать n членов. При этом последним платежом мы полностью гасим кредит, после чего долга не остаётся. Поэтому можно записать, что 
= 0.
Из условия, что остаток долга после каждого платежа уменьшается на одну и ту же величину, следует, что последовательность { } является убывающей арифметической прогрессией, состоящей из n членов. Если формально добавить к прогрессии «нулевой член» 
= C, то легко получить шаг прогрессии:
d = (
– 
)/ n = – C / n
С учётом этого прогрессия остатков долга будет выглядеть так:
= С (1 – 1/ n)
= С (1 – 2/ n)
…
= С (1 – m / n)
…
= С (1 – n / n) = 0 (2)
Теперь можно перейти к рассмотрению последовательности платежей. Поскольку ежемесячно остаток долга возрастает в соответствии с процентной ставкой r, а затем производится очередной платёж, то нетрудно понять, что размер этого платежа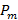 
будет представлять собой разность предыдущего остатка долга 
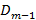, увеличенного на r %, и текущего остатка долга . Выражение для первого платежа получим, выразив 
формулы (1):
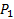= (1 + 0,01 r) C – 
= (1 + 0,01 r) –
И далее:
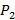= (1 + 0,01 r) –
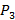= (1 + 0,01 r) – 
…
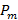= (1 + 0,01 r) –
…
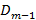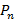= (1 + 0,01 r) 
– (3)
Подставляя выражение для из (2) в формулу (3) для 
, получим:
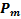= (1 + 0,01 r) C (1 – (m – 1)/ n) – C (1 – m / n) = (C / n)(1 + 0,01 r (n – m + 1)) (4)
Ввиду особой важности этой формулы, мы специально её выделили. Вместе с тем, промежуточные выкладки при её выводе для краткости опустили, полагая, что ученики 11-го класса способны выполнить соответствующие действия самостоятельно.
Формула (4) имеет ключевое значение для решения задач с кредитами, где предусмотрена дифференцированная система платежей. Поэтому её можно назвать основным уравнением задачи о кредитах с дифференцированными платежами.
Пользуясь полученным основным уравнением (4), при заданных параметрах кредита (C, n и r) легко вычислить размер платежа за любой месяц кредитного контракта. Например, если кредит на сумму 1 млн. рублей взят на 60 месяцев под 1% в месяц, то платёж за 11-й месяц (
) составит:
(1000000/60)(1 + 0,01*1(60 – 11 + 1)) = 25000 рублей.
Однако, чаще всего в задачах рассматриваемого типа требуется вычислить не размер разового платежа за тот или иной месяц кредитного контракта, а величину суммарного платежа за определённый период (например, в рассматриваемой задаче 1 речь идёт о сумме выплат за первые 12 месяцев). Обратим внимание, что основное уравнение (4) для 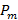линейно по m, причём m входит в него с отрицательным знаком. Отсюда следует, что последовательность { 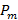}, как и { }, является убывающей арифметической прогрессией, состоящей из n членов. Поэтому выражение для 
получаем из стандартной формулы для суммы арифметической прогрессии:
= 
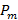+ )(m – k + 1)/2 (5)
Представляется нецелесообразным подставлять выражения для платежей из (4) в (5), переходя таким образом к общей буквенной формуле для , так как она получится достаточно громоздкой и неудобной для использования. Лучше сначала вычислить платежи за первый и последний месяцы заданного периода по формуле (4), а затем найти искомую сумму за весь период, используя (5).
Теперь мы можем легко решить задачу 1. Сначала найдём величины платежей за 1-й и 12-й месяцы контракта:
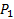= 2400000/24(1 + 0,01*3(24 – 1 + 1)) = 172000 руб.
= 2400000/24(1 + 0,01*3(24 – 12 + 1)) = 139000 руб.
А теперь получим окончательный ответ:
= (172000 + 139000)12/2 = 1866000 рублей.
Мы вместо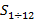 
пишем , поскольку при k = 1 удобнее записывать просто как 
.
***
Но отнюдь не всегда в задачах данного класса бывают заданы все основные параметры кредитного контракта (сумма кредита, срок и процентная ставка). Часто какой-либо из этих параметров требуется найти, при условии, что известны остальные параметры, а также сумма платежей за тот или иной период в течение срока кредитного договора.
Рассмотрим следующую задачу.
Задача 2. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что за последние 12 месяцев нужно выплатить банку 1130 тыс. рублей. Какую сумму планируется взять в кредит?
Здесь заданы n, r, а также 
(сумма платежей за второй год кредита, т.е., с 13-го по 24-й месяцы), а найти просят C. Как решить эту задачу? Сначала получим выражения для 
и 
, воспользовавшись основным уравнением (4):
= (C /24)(1 + 0,02(24 – 13 + 1)) = 1,24 C /24
= (C /24)(1 + 0,02(24 – 24 + 1)) = 1,02 C /24
Затем подставим их в формулу (5):
= (1,24 C /24 + 1,02 C /24)(24 – 13 + 1)/2 = 2,26 C /4 (6)
Из условия известно, что = 1130000 руб. Подставляя это число в левую часть выражения (6), легко находим сумму кредита C = 2000000 рублей. Задача решена.
***
Разберём ещё одну задачу.
Задача 3. В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после полного погашения составит 38 млн. рублей?
На этот раз заданы C и r, известна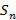 
, а найти требуется n. В данной задаче платёжным периодом является не месяц, а год, но никаких изменений в наши формулы это не вносит. Порядок всё тот же – сначала с помощью основного уравнения (4) находим 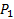и 
:
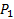= (16000000/ n)(1 + 0,25(n – 1 + 1)) = 16000000(1 + 0,25 n)/ n
= (16000000/ n)(1 + 0,25(n – n + 1)) = 16000000*1,25/ n
Подставляя эти выражения в (5), получаем:
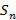= (16000000(1 + 0,25 n + 1,25)/2 n) n = 8000000(2,25 + 0,25 n).
С учётом условия 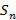= 38000000, приходим к уравнению
18 + 2 n = 38,
откуда находим ответ: n = 10 лет.
***
Встречаются задачи, где неизвестны два из трёх основных параметров кредитного контракта – и тем не менее, они тоже решаемы. Вот характерный пример:
Задача 4. 15-го января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма, взятая в кредит. Найдите r.
Здесь требуется найти размер процентной ставки, причём сумма кредита не задана. Зато известно, что общий объём выплат превышает сумму кредита на 15%, т.е. 
= 1,15 C. Порядок решения данной задачи будет несколько иным. Сначала запишем выражение для 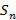, используя (5):
= 
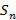= 9 
+ 
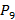)/2 (7)
В силу того, что { 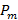} арифметическая прогрессия, + 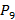)/2 будет равняться срединному члену { 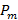}, т.е., 
. С учётом этого из (7) получим 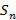= 9 , откуда, используя условие = 1,15 C, приходим к соотношению:
= 1,15 C /9 (8)
Используя основное уравнение (4), запишем выражение для :
= (C /9)(1 + 0,01 r (9 – 5 + 1)) = (C /9)(1 + 0,05 r) (9)
Приравнивая правые части уравнений (8) и (9), получаем 1 + 0,05 r = 1,15, откуда находим r = 3%.
***
Разобранными в данной работе примерами, конечно, не исчерпываются все возможные вариации задач о кредитах с дифференцированной системой платежей. Однако, не вызывает сомнения, что вдумчивый старшеклассник сможет самостоятельно с ними разобраться, используя технические приёмы, рассмотренные нами в настоящем методическом руководстве.
У читателя может возникнуть вопрос: неужели каждому выпускнику школы на экзамене придётся полностью воспроизвести представленные здесь рассуждения? Разумеется, нет. Это отняло бы слишком много времени и бумаги: ведь только решение задачи 1 заняло не менее двух страниц нашей методички. Но здесь мы постарались дать подробное текстовое описание решений, чтобы сделать их максимально понятными. На экзамене, конечно, имеет смысл аккуратно записать все формальные выкладки, которые не столь длинны. А текстовые пояснения следует давать лишь в отдельных местах, где это необходимо, и в как можно более сокращённом виде.