Учебный модуль 7. Последовательности и ряды. Тема 16. Функциональные ряды.
ЛЕКЦИЯ 16. Степенные ряды.
Функциональнымрядом называется ряд, членами которого являются функции от аргумента x
u 1(x) + u 2(x) + u 3(x) +... + un (x) +... =  (16.1)
(16.1)
Если в членах ряда (16.1) зафиксировать значение аргумента x = x 0, то получим числовой ряд
u 1(x 0) + u 2(x 0) + u 3(x 0) + un (x 0) +.... (16.2)
Если при x = x 0 числовой ряд (16.2) сходится, то x 0 называется точкой сходимости ряда (16.1).
Областью сходимости функционального ряда называется множество всех точек сходимости этого ряда. Если значение x 0 принадлежит области сходимости ряда (16.1), то можно говорить о сумме этого ряда в точке x = x 0:
u 1(x 0) + u 2(x 0) + u 3(x 0) + un (x 0)... = S (x 0).
Значение суммы функционального ряда зависит от значения переменной x, т.е. сумма функционального ряда S (x) является функцией переменной x.
Степенным рядом по степеням x называется функциональный ряд вида
 (16.3)
(16.3)
где а 0, а 1,... аn,... не зависят от x и называются коэффициентами ряда.
Степенной ряд (16.3) всегда сходится, по крайней мере, в точке x = 0. При любых конкретных x = x 0 ряд (16.3) становится числовым рядом
 (16.4)
(16.4)
Степенной ряд (16.4) сходится в точке x 0 абсолютно, если сходится ряд, образованный из модулей членов числового ряда

Найдем область сходимости ряда (16.3), используя признак Даламбера для положительных числовых рядов. По этому признаку ряд (16.3) сходится, если

Следовательно, ряд (16.3) заведомо сходится если 
и расходится при  . Величина
. Величина
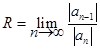 (16.5)
(16.5)
называется радиусом сходимости степенного ряда (16.3). Ряд заведомо сходится в интервале ½ x ½ < R или - R < x < R, который называется интервалом сходимости. Признак Даламбера ничего не говорит о сходимости ряда в точках х =  В этих точках сходимость ряда надо исследовать отдельно.
В этих точках сходимость ряда надо исследовать отдельно.
Исследовать степенной ряд на сходимость означает найти его интервал сходимости и установить сходимость или расходимость ряда в граничных точках интервала, т.е. при x = R и x = -R. Присоединив граничные точки, в которых ряд сходится, к интервалу сходимости получим область сходимости степенного ряда.
Пример 1. Найти область сходимости ряда

Решение. 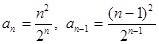 . Используя формулу (16.5), получим
. Используя формулу (16.5), получим

Интервал сходимости данного ряда характеризуется неравенством ½ x ½ < 2. Исследуем сходимость ряда в граничных точках x = ± 2. Подставим x = ± 2 в исходный ряд, получим
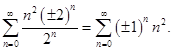
Оба эти ряда расходятся, так как не выполняется необходимое условие сходимости численных рядов  , а не к нулю. Следовательно, область сходимости данного степенного ряда совпадает с интервалом сходимости.
, а не к нулю. Следовательно, область сходимости данного степенного ряда совпадает с интервалом сходимости.
Пример 2. Найти область сходимости ряда

Решение. Так как 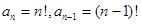 , то
, то

то ряд сходится при всех конечных значениях x, т.е. -¥ < x <¥.
Пример. Найти область сходимости ряда
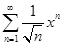
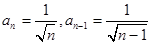
 ,
,
так как 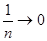 при
при  .
.
Интервал сходимости  или
или 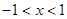 . Исследуем отдельно точки
. Исследуем отдельно точки  . При
. При 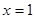 исходный степенной ряд имеет вид
исходный степенной ряд имеет вид
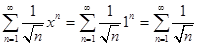 ,
, 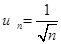
Этот ряд относится к обобщенным гармоническим и, как было показано в предыдущем разделе, он расходится.
При 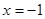
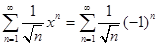 . Это знакочередующийся ряд. Его сходимость проверяется по теореме Лейбница.
. Это знакочередующийся ряд. Его сходимость проверяется по теореме Лейбница.
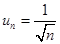 >
> 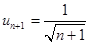 и
и  , если
, если  .
.
Ряд сходится. Область сходимости 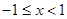 или
или 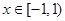 .
.
Основные свойства степенных рядов.
1) Во всех точках, лежащих внутри интервала сходимости, сумма степенного ряда является непрерывной функцией переменной x:
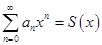
2) Степенной ряд можно почленно интегрировать внутри интервала сходимости:
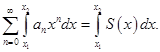
3) Внутри интервала сходимости степенной ряд можно почленно дифференцировать:

При почленном интегрировании и дифференцировании степенных рядов их интервалы сходимости не меняются.
Пример. Найти сумму ряда
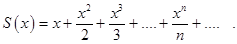 (16.6)
(16.6)
Решение. Найдем сначала интервал сходимости этого ряда 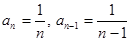 ,
,

Следовательно, интервал сходимости ряда (-1, +1). Продифференцировав (16.6), имеем
S¢ (x) = 1 + x + x 2 +... + xn +....
Правая часть этого выражения - геометрический ряд q = x, который сходится при ½ x ½< 1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим
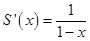
Отсюда сумму исходного ряда найдем интегрированием
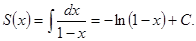
Найдем C. Из (16.6) следует, что S (0) = 0. Следовательно,
0 = - ln (1-0) + C, C = 0.
Таким образом, S (x) = - ln (1- x) = 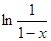
 .
.
Ряды по степеням (х – а). Наряду со степенными рядами относительно переменной х часто рассматривают степенные ряды по переменной (x-a), т.е. ряды вида
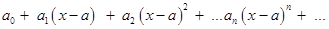 (16.7)
(16.7)
Этот ряд подстановкой y = (x - a) превращается в ряд типа (16.3). Поэтому, если степенной ряд (16.3) имеет интервал сходимости - R < x < R, то соответствующий ряд вида (16.7) имеет интервал сходимости (a - R) < x < (a + R), центр которого расположен в точке x = a.
Пример. Найти интервал сходимости следующего ряда
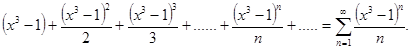
Решение. Найдем радиус сходимости ряда. 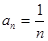 ,
, 

Отсюда -1 < (х 3 -1) < 1 или 0 < x 3 < 2.
Следовательно, интервал сходимости ряда 0 < x < 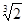 .
.
Ряд Тейлора. Пусть функция f (x) в точке х = а имеет производные любого порядка. Если имеется сходящийся степенной ряд
 =
= 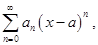 (16.8)
(16.8)
сумма которого равна функции f (x), т.е.
 , (16.9)
, (16.9)
то найдем коэффициенты такого ряда. Очевидно, что f (a) = а 0. Продифференцировав (16.9) в точке х = а, имеем а 1= f ¢(a). Продифференцировав (16.9) в точке х=а дважды, получим 2 а 2 = f ¢¢(a) или  . Продолжая дифференцирование, можно убедится, что коэффициенты ряда (16.9) находятся по формуле
. Продолжая дифференцирование, можно убедится, что коэффициенты ряда (16.9) находятся по формуле  , где
, где  производная порядка вычисленная в точке а.
производная порядка вычисленная в точке а.
Степенной ряд вида
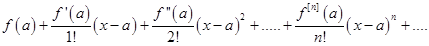
называется рядом Тейлора для функции f (x).
В частном случае при a = 0 ряд Тейлора имеет вид
f (x) = 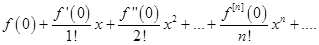
и его называют рядом МакЛорена.
При помощи рядов Тейлора и МакЛорена можно вычислить значение любой функции в точке с необходимой точностью.
Пример. Разложить в ряд Тейлора функцию f (x) = ex.
Поскольку ex =(ex)¢=(ex)¢¢ =...(ex)[ n ], то при x = 0 для f (x)= ex имеем
f (0) = 1; f ¢(0) = 1; f ¢¢(0) = 1;...; f [ n ](0) = 1;....
Следовательно, ряд Тейлора функции y = ex в окрестности точки x =0 имеет вид
ex = 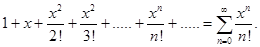 (16.10)
(16.10)
Ряд (16.10) сходится на всей числовой оси к функции y = ex (см. пример 2). Вычислим по формуле (16.10)  . Подставим в (16.10)
. Подставим в (16.10) 

По четырем первым слагаемым мы получили ответ с точностью до тысячных.
Пример. Разложить в ряд МакЛорена функцию f (x) = sin x.
Решение. Для функции sin x имеем:
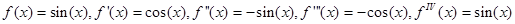 …
…
В точке ноль а = 0

Следовательно, ряд МакЛорена для sin x:
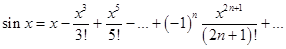
или

Аналогично получается разложение для функции cos x:
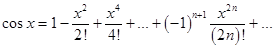
или
cos x =  .
.
Подобным образом можно получить разложения в ряд Тейлора и многих других функций.