Сопряжение прямых линий
При пересечении прямые линии образуют острый, прямой или тупой угол.
Задача: сопряжение двух пересекающихся прямых m и n дугой окружности заданного радиуса R
Решение:
1. найти (начертить) биссектрису угла
Биссектриса (угла) - это луч с началом в вершине угла, делящий угол на две равные части.
«Биссектриса» – слово латинского происхождения, состоящее из двух частей: «bi» – «пара, двойное» и «sectio» – «разрезать, делить». Название отражает суть: деление чего-то пополам, то есть на две равные части
Для нахождения биссектрисы можно:
- использовать транспортир.
- выполнить графическое построение с помощью циркуля
Дано: ÐА. символ угол Ð
С помощью циркуля строим окружность произвольного радиуса с центром в вершине 
А.
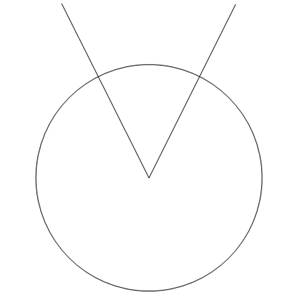
Точки пересечения данной окружности со сторонами А обозначим В и С.
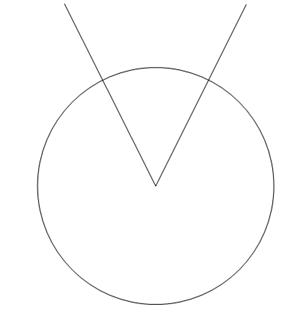
Теперь проведем две окружности одинакового радиуса ВС с центрами в точках В и С.
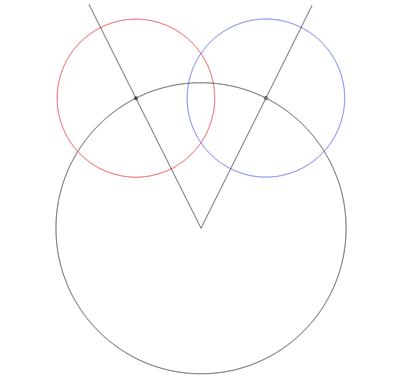
получим одну или две точки пересечения данных окружностей внутри А.
проводим с помощью линейки луч с началом в точке А.
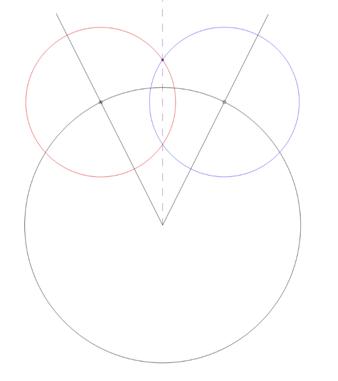
Результат
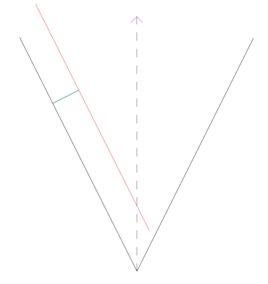
2. При сопряжении двух пересекающихся прямых m и n дугой окружности заданного радиуса Rцентр О сопрягающей дуги находится на биссектрисе угла и отстоит от сторон угла на расстоянии, равном радиусу сопрягающей дуги,
т.е. в пересечении двух вспомогательных прямых m′ и n′(рис. 3, а).
2.1. Проведем вспомогательную линию m′ параллельно линии m на расстоянии R
2.2. Проведем вспомогательную линию n′ параллельно линии n на расстоянии R
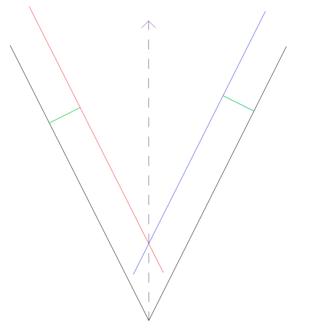
2.3. центр О сопрягающей дуги находитсяв пересечении двух вспомогательных прямых m′ и n′
2.4. Для получения точек сопряжения и T1иТ2из центра О на прямые m и n опускаются перпендикуляры.
|
|
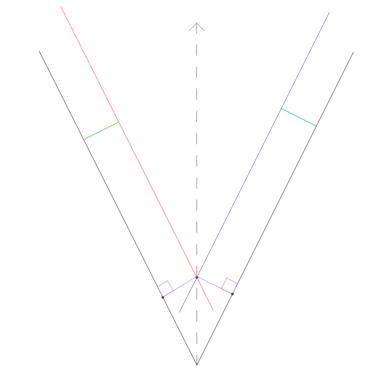
2.5. Радиусом Rиз центра О проводится сопрягающая дуга Т1Т2.
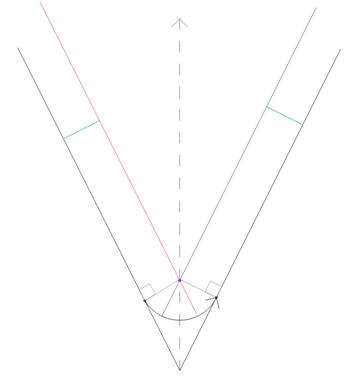
Результат.
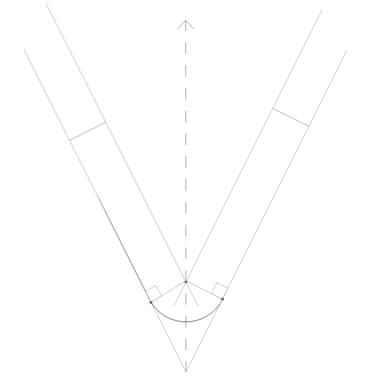
На рисунке 3, б показано построение сопряжения архитектурного облома «полочка». При заданной точке сопряжения T1 для нахождения центра О сопрягающей дуги из T1 опускается перпендикуляр к прямой n и на нем откладывается отрезок OT1 =R.
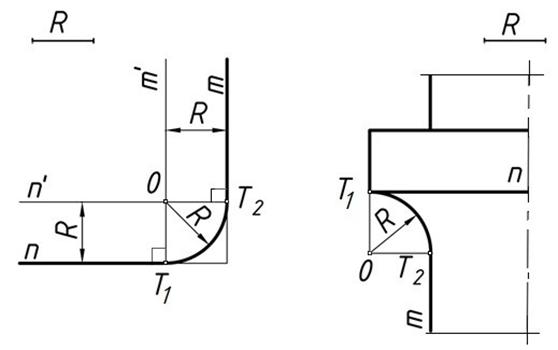
а б
Рис. 3
Точка сопряжения Т2 находится на перпендикуляре, опущенном из центра О на прямую m.
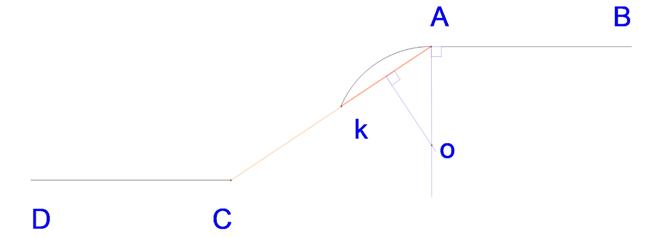
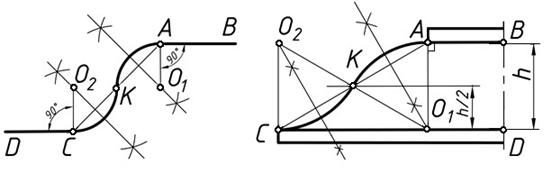
Построение сопряжения двух параллельных прямых АВ и DС дугами окружностей
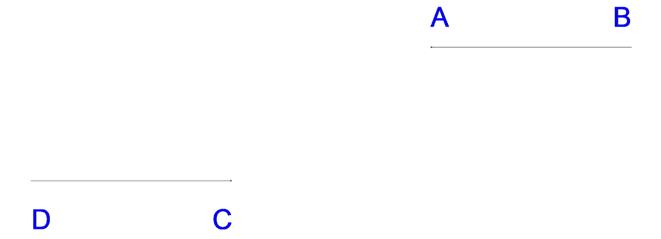
точки А и С соединяются прямой и на ней выбирается точка касания К сопрягающих дуг
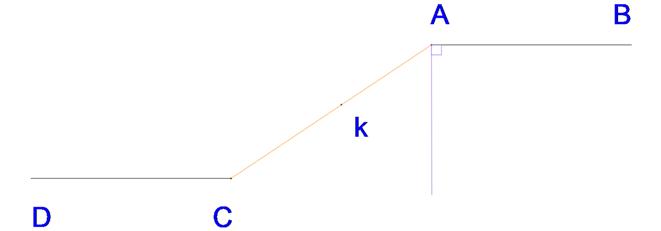
Прямая АВ будет касательной к сопрягающей дуге окружности, а точкаА – точкой касания.
Следовательно, центр O1 сопрягающей дуги должен лежать на перпендикуляре AO1, восстановленном из точки А к прямой АВ.
Отрезок АК – хорда сопрягающей дуги, следовательно, центр этой дуги должен находиться на перпендикуляре, проведенном через середину хорды АК.
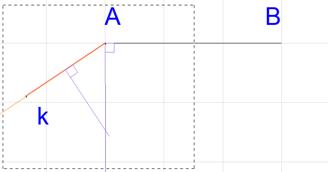
Центр О1 сопрягаемой дуги определятся точкой пересечения этих двух перпендикуляров.
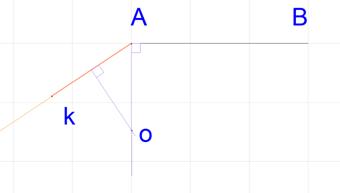
Аналогично определится и центр О2 второй сопрягающей дуги СК. Точка К может иметь различные положения на прямой АС.
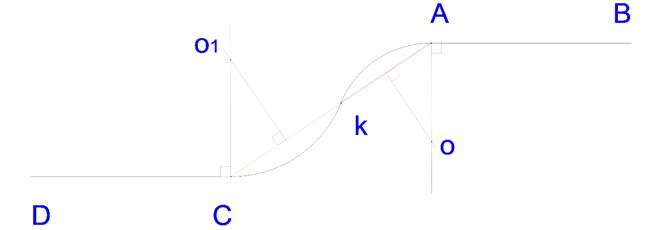
На рисунке 4, б (элемент вазы) точка К располагается в середине отрезка АC, нахождение центров О и О1, точек касания Aи C ясно из чертежа.
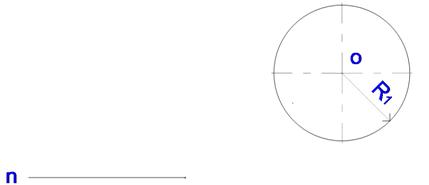
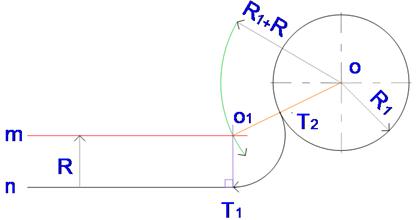
Сопряжение прямой линии с окружностью
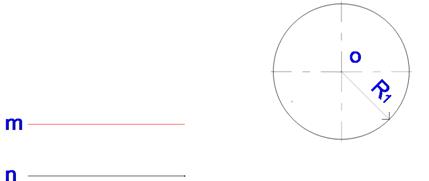
Дано: прямая n, окружность радиуса R1 (центр О),
нужно соединить прямую и окружность дугой радиуса R
|
|
Построение сопряжения прямой n и окружностирадиуса R1
При касании двух окружностей точка их касания находится на пересечении окружностей с линией, соединяющей их центры.
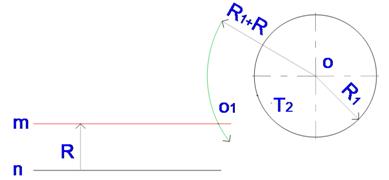
На расстоянии, равном радиусу R, от прямой n проводят прямую m параллельно n.
Из центра заданной окружности радиуса R1строят вспомогательную дугу окружности радиусом R1 + R2.
Пересечение этой дуги и прямой m определит центр O1сопрягающей дуги.
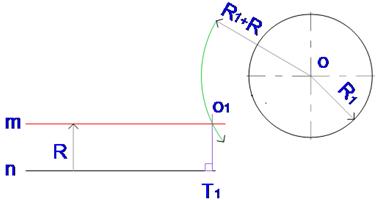
Точка касания T1будет лежать на пересечении перпендикуляра, опущенного из центра O1 на прямую n.
Вторая точка касания располагается на пересечении заданной окружности и линии, соединяющей центры О и О1
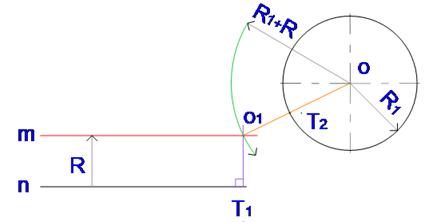
Проведите дугу сопряжения прямой и окружности. Результат.
а б
Рис. 5
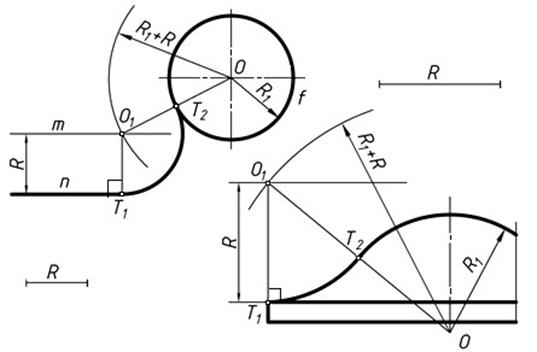
На рисунке 5, б показано применение данного сопряжения на элементе вазы.
На рисунке 6 приведено построение данных сопряжений на двух характерных элементах вазы «торус».
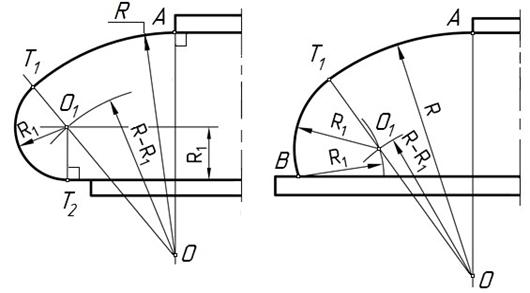На рисунке 6, а дуга окружности радиусом R1сопрягает дугу R сгоризонтальной прямой. Положение точек касания Т1 иТ2 понятно из построения.
На рисунке 6, б построено сопряжение горизонтальной прямой и дуги R с заданным положением точек касания А и В. Радиус сопряжения равен R1.