Филиал РГГУ в г. Домодедово
Кафедра математических и естественнонаучных дисциплин
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельного приобретения знаний и овладения умениями
По дисциплине
МЕТОДЫОПТИМАЛЬНЫХ РЕШЕНИЙ
(направление ЭКОНОМИКА)
(Бесконтактная форма обучения)
Практическое занятие 2
Тема: Принятие решений по выбору оптимальных путей в топологических структурах
Время: 4 часа
Разработал профессор СМИРНОВ В.Е.
Домодедово 2019
Практическое занятие
Тема: Принятие решений по оптимизации потоков в сетях на основе методов теории графов
Время: 4 часа (2 + 2 СР)
1. Теоретическая часть Задача о кратчайшем пути
Задание 1. Изучить метод Дейкстры (метод получения кратчайших путей)
Пусть задана некоторая совокупность географически разнесенных пунктов, связанных между собой автомобильными или железными дорогами, газовыми или нефтяными магистралями, коммуникационными линиями и т.п. При планировании доставки грузов, топлива, сообщений и пр. возникает задача, доставки их по наиболее коротким, а следовательно и более дешевым, путям из одного пункта сети в другой.
Такая совокупность пунктов вместе с соединяющими их магистралями формально может быть представлена в форме плоского графа, в котором дуги соответствуют магистралям, а вершины – пунктам отправки и доставки. Граф может быть как ориентированным так и неориентированным. При этом каждой дуге графа может поставлено в соответствие неотрицательное число lij – «длина» дуги. Под «длиной» дуги понимается любая физическая величина - расстояние, время, стоимость и т.д.
Часто требуется на графе G получить кратчайший путь – путь наименьшей длины из вершины X0 в вершину Xn, а также уметь вычислять все кратчайшие пути из одной вершины во все остальные.
В качестве исходных данных для реализации алгоритма задается размеченный граф, на котором указаны «длины» всех дуг. Результатом расчетов должны быть кратчайшие пути и их длины.
Для решения таких задач разработано несколько методов (алгоритмов). Рассмотрим один из них – алгоритм Дейкстры.
Задача с использованием алгоритма Дейкстры реализуется в два этапа. На первом этапе определяются кратчайшие длины путей из вершины истока до всех остальных вершин в графе. На втором этапе по промежуточным результатам первого этапа строится дерево кратчайших путей из вершины истока до всех остальных вершин в графе.
Алгоритм реализуется по шагам, в два этапа.
Этап 1.Вычисление кратчайших путей
Шаг 1. Присвоить вершине истоку длину пути равную нулю (L(Xи) = 0). Определить длины путей до всех смежных с вершиной истоком вершин. Запомнить длины всех непосредственных путей.
Шаг 2. Рассмотреть одну из непосредственно связанных с истоком вершин. Петлевые пути отбросить. Рассчитать длины путей до всех остальных непосредственно связанных вершин. Кратчайшие пути запомнить, более длинные пути отбросить.
Шаг3, 4, …, n-1. Повторять шаг 2 для всех вершин графа.
Этап 2. По полученным на первом этапе данным построить дерево путей.
Рассмотрим применение алгоритма Дейкстры на конкретном примере.
Пример 1. Требуется определить кратчайшие пути из вершины X0 (истока) во все остальные вершины графа, изображенного на рис.1. Числа над дугами отражают длину этих дуг.
| х1 |
| х2 |
| х3 |
| х4 |
| х0 |
| х3 |
Рисунок 1 – Исходный неориентированный граф
Для получения всех кратчайших путей из вершины Х0 (исток) до всех остальных вершин графа воспользуемся визуальным представлением алгоритма. Алгоритм выполняется по шагам. Общее число шагов равно n-1 (n - число вершин в графе).
Этап 1.
Шаг 1. Присвоим вершине Х0 значение длины пути равное нулю (L0 = 0). У вершины Х0 имеется три инцидентных дуги (Х0 –Х1), (Х0-Х2), (Х0-Х3) – (рис..2). Длины дуг соответственно равны 2, 6, 7.
| Х0 L0 = 0 |
| Х1 L1(x0) = 0 +2 = 2 |
| Х2 L2(x0) = 0 +6 = 6 |
| Х3 L3(x0) = 0 +7 = 7 |
Рисунок- 2- Шаг 1
Шаг 2. Рассмотрим вершину Х1. Значение длины пути в Х1 из вершины Х0 равно 2 (L1(х0) = 2). У вершины Х1 имеется три инцидентных дуги (Х1–Х0), (Х1-Х2), (Х1-Х4) – (рис.3). Дуга (Х1 –Х0) образует петлю, поэтому ее исключим из рассмотрения. Длины других дуг соответственно равны 3, 6.
| Х1 L1(Х0)= 2 |
| Х0 L1(x1) |
| Х2 L2(x1) = 2 + 3 = 5 |
| Х4 L4(x1) = 2 +6 = 8 |
| L2(x0) (шаг 1) - отбрасываем. |
| Новый - оставляем. |
Рисунок- 3- Шаг 2
Шаг 3. Рассмотрим вершину Х2. Значение длины пути в Х2 из вершины Х0 равно 5 (L2(х5) = 5 – шаг 2). У вершины Х2 имеется три инцидентных дуги (Х2–Х0), (Х2-Х1), (Х2-Х4) – (рис.4). Дуга (Х1 –Х0) образует петлю, поэтому ее исключим из рассмотрения. Длины других дуг соответственно равны 3, 5.
| Х2 L2(Х0)= 5 |
| Х0 L2(x0) |
| Х1 L1(x2) = 5 +3 = 8 |
| Х4 L4(x2) = 5 +5= 10 |
| Петля - отбрасываем |
| L2(x2) < L2(x0) - оставляем |
| Петля - отбрасываем |
| L4(x2) > L4(x1) -отбрасываем. |
| L1(x2) > L1(x0) - отбрасываем |
Рисунок- 4- Шаг 3
Шаг 4. Рассмотрим вершину Х3. Значение длины пути в Х3 из вершины Х0 равно 7 (L3(х0 = 1 – шаг 1). У вершины Х2 имеется две инцидентных дуги (Х3–Х0), (Х3-Х4) – (рис.5). Дуга (Х1 –Х0) образует петлю, поэтому ее исключим из рассмотрения. Длина дуги (Х3-Х4) равна 4.
| L4(x3) > L4(x1) -отбрасываем. |
| Х3 L3(Х0) =7 |
| Х0 L3(x0) |
| Х4 L4(x3) = 7 +4 = 11 |
| Петля - отбрасываем |
Рисунок -5 Шаг 4
Этап 2. Построение дерева кратчайших путей
Путь 1. (Х0 – Х1) - дуга непосредственной связи (Х0 – Х1), L1 = 2 (шаг 1).
Путь 2. (Х0 – Х1 – Х2), L2 = 5 (шаг 2).
Путь 3. (Х0 – Х3) - дуга непосредственной связи (Х0 – Х3), L1 = 7 (шаг 1).
Путь 4. (Х0 – Х1 – Х4), L4 = 8 (шаг 2).
Таким образом, дерево кратчайших путей принимает вид, показанный на рис. 6.
| х0 |
| х1 |
| х2 |
| х3 |
| х4 |
| Х0 | Х1 | Х2 | Х3 | Х4 |
Рисунок 6 - Дерево кратчайших путей
Важным достоинством алгоритма Дейкстры является то, что он с незначительной модификацией позволяет формально вычислять не только кратчайшие пути в графе, но и наибольший из всех полных путей, т.е. критический путь, что позволяет использовать его в сетевых графиках. Основным же достоинством данного метода является то, что он за один проход позволяет получить все кратчайшие пути из принятой вершины истока во все остальные вершины графа.
К недостаткам метода можно отнести то, что он позволяет вычислять все кратчайшие пути только из одной определенной вершины (принятого истока). Этого недостатка лишен метод Флойда, который позволяет вычислять все кратчайшие пути между любыми вершинами графа.
Практическая часть
Задание 2. (выполняется самостоятельно по вариантам).
Варианты 1-8. Требуется определить кратчайшие пути из вершины Xi (истока) во все остальные вершины на графе, изображенном на рис.7. Числа над дугами отражают длину этих дуг.
Таблица вариантов
| Вариант | ||||||||
| Исток (i) | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
Варианты 9-17. Требуется определить кратчайшие пути из вершины Xi (истока) во все остальные вершины на графе, изображенном на рис.8. Числа над дугами отражают длину этих дуг.
Таблица вариантов
| Вариант | |||||||||
| Исток (i) | X0 | X1 | X2 | X3 | X4 | X5 | X5 | X7 | X8 |
| х0 |
| х1 |
| х2 |
| х5 |
| х1 |
| х4 |
| х7 |
| х6 |
| х8 |
| х3 |
Рисунок 7- Граф для вариантов 1-8
| х0 |
| х1 |
| х2 |
| х5 |
| х1 |
| х4 |
| х7 |
| х6 |
| х8 |
| х3 |
Рисунок 8- Граф для вариантов 9-17
Варианты 18-26. Требуется определить кратчайшие пути из вершины Xi (истока) во все остальные вершины на графе, изображенном на рис.9. Числа над дугами отражают длину этих дуг.
Таблица вариантов
| Вариант | |||||||||
| Исток (i) | X0 | X1 | X2 | X3 | X4 | X5 | X5 | X7 | X8 |
| х0 |
| х1 |
| х2 |
| х5 |
| х1 |
| х4 |
| х7 |
| х6 |
| х8 |
| х3 |
Рисунок 9 Граф для вариантов 18-26
Теоретическая часть. Потоки в сетях
Задание 3. Изучить методы вычисления потоков в сетях
Пусть задана некоторая совокупность географически разнесенных пунктов, связанных между собой автомобильными или железными дорогами, газовыми или нефтяными магистралями, коммуникационными линиями и т.п. При планировании доставки грузов, топлива, сообщений и пр. возникает задача организации максимального потока (например, максимального количества грузов в единицу времени) из одного пункта в другой с учетом того обстоятельства, что пропускная способность каждой магистрали есть величина ограниченная.
Такая совокупность пунктов вместе с соединяющими их магистралями формально может быть представлена в форме плоского графа, в котором дуги соответствуют магистралям, а вершины – пунктам отправки и доставки. Граф может быть, как ориентированным так и неориентированным. При этом каждой дуге графа может поставлено в соответствие неотрицательное число с ij – «пропускная способность» дуги (максимальное количество вещества, которое может пропустить данная дуга в единицу времени).
Если какая – либо пара вершин I,J не соединена между собой непосредственной связью (дугой), то полагают, что cij = 0. Кроме того, полагают, что если в сеть входит дуга (Xi,Xj), то в нее входит и симметричная ей дуга (Xj,Xi), но пропускные способность этих дуг могут быть различными, т.е. cij ≠ сji.
Потоком zij по дуге (Xi,Xj) называется количество вещества, проходящее через эту дугу в единицу времени. Потоком по сети (просто потоком) называют совокупность {zij} по всем дугам сети.
Будем считать, что потоки удовлетворяют следующим требованиям:

 , (3.1)
, (3.1)
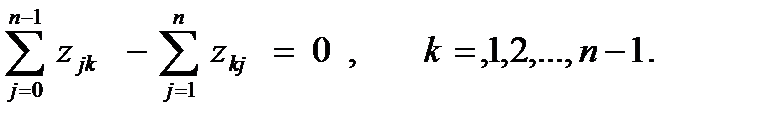 (3.2)
(3.2)
Ограничения (3.1) означают, что потоки по любой дуге неотрицательны и не превышают их пропускных способностей.
В уравнениях (3.2) уменьшаемая сумма z0k + z1k + … + zn-1k представляет количество вещества, притекающего в вершину Xk по всем, входящим в эту вершину дугам (если из Хi в Хk дуга не входит, то zik = 0). Вычитаемая же сумма zk1 + zk2 + … + zkn представляет собой количество вещества, вытекающего из вершины Х по всем выходящим из этой вершины дугам (аналогично, если из Хk в Хj дуга не входит, то zkj = 0).
Таким образом, ограничения (3.2) означают, что количество вещества, втекающего в любую (произвольную) вершину сети (кроме истока Х0 и стока Хn), равно количеству вещества, вытекающего из этой вершины. Поток, удовлетворяющий ограничениям (3.1) и (3.2) называется допустимым.
Из ограничений (3.2) следует, что общее количество вещества  , вытекающего из вершины истока Х0, совпадает с общим количеством вещества
, вытекающего из вершины истока Х0, совпадает с общим количеством вещества  , втекающим в вершину стока Xn, т.е.
, втекающим в вершину стока Xn, т.е.
 =
=  = w. (3.3)
= w. (3.3)
Линейная функция w - (3.3) - называется величиной потока в сети.
Таким образом, задача о максимальном потоке в сети представляет собой задачу линейного программирования: среди всех решений системы линейных ограничений (3.1),(3.2) следует получить такое решение, которое максимизирует целевую функцию (3.3). Такое решение z*ij называется максимальным потоком в сети.
Как и любая задача линейного программирования, задача о максимальном потоке может быть решена симплекс-методом, но особенности постановки этой задачи позволили разработать для ее решения более простые специальные методы. Одним из таких методов (алгоритмов) является алгоритм Форда -Фалкерсона.