Свойства неопределённого интеграла
1.Линейность операции интегрирования
2.Инвариантность формул интегрирования
Это очень важное свойство, поскольку позволяет расширить возможности таблицы. Любая формула интегрирования остаётся справедливой, если независимую переменную x заменить любой дифференцируемой функцией x(t):
На применении этих свойств основано так называемое непосредственное интегрирование. Например:
При этом на первом шаге было использовано свойство линейности интеграла. После чего второе слагаемое–это табличный интеграл (формула №9). А для первого слагаемого применено свойство инвариантности, где в качестве функции x(t) используется 
. Это позволяет «увидеть» здесь табличную формулу 2.
Такой приём ещё называют подведением функции под знак дифференциала. Название отражает известное свойство дифференциала
.
Для нашего примера его можно записать как
.
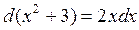Для того, чтобы научиться интегрировать, необходимо освоить основные методы, уметь их технически выполнять и знать, в каком случае «работает» соответствующий метод.
Интегрирование по частям
Этот метод состоит в применении формулы
.
При этом функции u=u(x), v=v(x) имеют непрерывные производные. Выбор «частей» для подынтегрального выражения, стоящего в левой части равенства, обусловлен всего лишь очевидным требованием: интеграл, который получится в правой части, должен быть более простым. Применять этот метод можно в различных случаях. Чаще всего тогда, когда подынтегральная функция является произведением рациональной и функции какого-то другого класса. Например:
=
В квадратных скобках указывают необходимые вычисления. В левом столбце записано разбиение подынтегрального выражения на части, чем и обусловлено название метода. А в правом просто найдены величины, нужные для применения формулы.
Замена переменной в неопределённом интеграле
Этот метод предполагает введение новой переменной с целью сделать интеграл известным или даже табличным. Новая переменная выбирается исходя из конкретного вида подынтегральной функции. В общем случае это означает выбор функции 
Эта функция предполагается дифференцируемой и осуществляющей взаимно однозначное соответствие между переменными x и t в рассматриваемых областях их изменения. Такое требование обеспечивается, если 
строго монотонна и дифференцируема. Выбрав подходящую для подстановки функцию, исходный интеграл записывают в виде
Здесь g(t)= 
, а интеграл 
предполагается известным. Для записи окончательного ответа выполняется обратный переход от переменной t к переменной x.
Например:
Интегрирование рациональных функций
В общем случае рациональная функция представляет собой частное двух многочленов, а значит дробь. Общий вид таких дробей записывают
.
Здесь 
и 
-многочлены соответственно n и m степеней по переменной x. В зависимости от соотношения показателей старшей степени этих многочленов дроби различают на правильные и неправильные. Если n<m, то дробь называется правильной. В остальных случаях 
дробь неправильная. Приступая к работе с интегралом вида
нужно сначала выяснить, какая именно дробь здесь рассматривается. Если дробь неправильная, её следует представить в виде суммы многочлена и правильной рациональной дроби. Этот процесс называется выделением из дроби целой части и в общем случае осуществляется делением с остатком числителя на знаменатель «углом». Например:
Если в исходном интеграле дробь была правильной,то этот шаг пропускаем. Таким образом, поскольку целая часть представляет собой многочлен и его интегрирование проблем не вызывает, в любом случае вопрос сводится к интегрированию правильной рациональной дроби.
Из алгебры известно, что всякая правильная рациональная дробь может быть представлена как сумма конечного числа элементарных (простейших) дробей четырёх типов:
Здесь A,B,a,p,q – вещественные числа, k - натуральное. Квадратные трёхчлены в знаменателях дробей третьего и четвёртого типов действительных корней не имеют.
Практическое применение этого утверждения начинается с разложения знаменателя правильной дроби на множители. Разложение выполняется до линейных и квадратичных множителей (с отрицательным дискриминантом). Например, в нашем случае получается 
. Каждый из сомножителей в полученном произведении порождает впоследствии простейшую дробь соответствующего типа. Нужно просто сравнить его со стандартом и выбрать соответствующий тип. В данном примере, очевидно, каждый из сомножителей имеет вид 
Поэтому в разложении правильной дроби следует записать три слагаемых первого типа. Знаменателем каждой из простейших дробей будет один из сомножителей. Числитель всегда записывается в соответствии с выбранным типом стандарта. Для первого типа он представляет собой число, пока неизвестное, а потому обозначенное буквой А. Называются эти числа неопределёнными коэффициентами. Итак, в данном случае разложение дроби на простейшие имеет вид:
Для нахождения стоящих в правой части неопределённых коэффициентов A, B, и C составляется система уравнений. Очевидно, в нашем примере этих уравнений должно быть три (по числу неизвестных). Для составления системы уравнений есть два варианта. Если все дроби в разложении получились первого типа, то лучше применять метод частных значений. Он основан на том факте, что равенство
должно выполняться при любом значении x. Для нас это означает, что можно подставить в данное равенство те значения x, при которых будет удобно считать. Очевидно, это те значения х, при которых некоторые слагаемые в правой части обращаются в нуль. В результате такой подстановки 
получается система из трёх уравнений с тремя неизвестными:
Такая система разрешима всегда. Её решение даёт возможность записать наш интеграл в виде суммы табличных интегралов с известными коэффициентами:
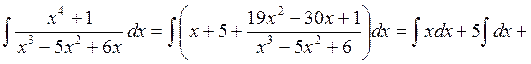
Умение интегрировать рациональные функции является основным. Потому что многие выражения удаётся, как это называется, рационализировать с помощью подходящих подстановок. В результате получается интеграл от рациональной дроби, а его можно взять всегда.