Волновая функция Ψ — это центральное понятие в к. механике, описывает к. состояние изолированной системы из одной или нескольких частиц. Т.е. одна волновая функция описывает состояние всей системы, а не отдельные функции на каждую частицу.
Волновая функция — это комплекснозначимая функция степеней свободы системы, непрерывная или дискретная.
Множество волновых функций системы образуют функциональное Гильбертово пространство (пространство называется Гильбертовым, если оно полное, и на нём определено внутреннее произведение [произведение двух векторов, дающее скаляр]). А внутреннее произведение — это мера наложения между физическими состояниями (соответствие между вероятностями перехода между физическими состояниями и внутренним произведением задаётся правилом Борна).
Развитие волновой функции по времени задаётся уравнением Шрёдингера (аналог 2го закона Ньютона, F = m a, в классической механике):
где i – мнимая единица, ħ — постоянная Планка, делённая на 2π, ∂/∂t - частная производная по времени, Ψ - волновая функция системы, Ĥ - Гамильтониан (оператор, характеризующий полную энергию волновой функции).
Математически, уравнение Шрёдингера — разновидность волнового уравнения. Отсюда корпускулярно-волновой дуализм — т. е. система, описываемая таким образом, ведёт себя как волна. (однако, волна эта — не как физическая волна, например жидкости, а волна в абстрактном математическом пространстве).
Значения волновой функции (комплексные числа) сами-по-себе ничего не говорят о величинах и направлениях наблюдаемых. Нужно применить к волновой функции квантовый оператор, чьи собственные значения соответствуют множеству возможных результатов
измерения, и вычислить статистическое распределение измеряемой величины.
Собственные вектора и значения:
Если Ax=λx, то x — собственный вектор, а λ — соответствующее ему собственное значение матрицы A (или соответствующего линейного преобразования A). Геометрически, это означает что при преобразовании A вектор x не меняет своего направления, только растягивается на величину λ.
Измерение:
Проблема квантового измерения в том, что квантовое состояние, в котором измеряется наблюдаемая величина — неопределённо. Оно мыслится как суперпозиция собственных состояний наблюдаемой — состояний, в которых наблюдаемая уникально определена. (например, спин электрона — вверх, или вниз).
Т.е. нам недоступны все λi – мы можем только измерить состояние — и с вероятностью | λi| 2 получим некоторое базовое состояние |i>.
Когда осуществляется измерение состояния квантовой системы – система (по Копенгагенской интерпретации) перепрыгивает в одно из собственных состояний системы (это называется коллапс волновой функции), возвращая собственное значение, соответствующее этому состоянию. Суперпозиция состояний даёт им неодинаковые веса — чем больше вес данного состояния, тем выше вероятность, что именно оно будет измерено.
По Многомировой интерпретации, состояние системы не коллапсирует при измерении — а мы попадаем в ту или иную возможную Вселенную, где реализуется этот вариант состояния.
По Теории де Бройля — Бома состояние системы строго определённо в каждый момент времени. Эволюция конфигурации во времени задаётся с помощью «задающего уравнения» (даже при отсутствии наблюдателя) - при измерении одной частицы оно моментально задаёт положения всем остальным. Это, очевидно, нелокальная теория.
По Теории декогеренции, при взаимодействии со средой, квантовая система неизбежно теряет информацию необратимым образом (информация «утекает» в среду) — вследствие того что компоненты квантовой системы расцепляются, и сцепляются с элементами среды. Это не вызывает «действительный» коллапс волновой функции — мы только наблюдаем это как коллапс, вследствие утечки информации в среду. В то время как «глобальная» волновая функция (нашей квантовой системы + среды) сохраняется.
По Закону Борна, результат измерения наблюдаемой, соответствующей оператору A, в системе с волновой функцией ψ, будет одним из собственных значений A. И вероятность, что будет измерено данное λi - равна | <λi|ψ>| 2.
Запутанность — это нелокальное свойство, позволяющее множеству кубитов испытывать большую степень соотношения, чем это возможно в классических системах. Иными словами, запутанность не зависит от расстояния между частицами, в отличие от классических феноменов — таких как ядерные, гравитационные или электромагнитные поля.
Например, два запутанных кубита в состоянии Бэлла (равная суперпозиция):
1/√2(|00>+|11>)
имеют равную вероятность, что измерение даст |00> или |11>.
Теперь разделим эти два кубита, и один дадим Алисе, а другой Бобу. Алиса измеряет свой кубит, и получает с равной вероятностью |0> или |1>. Теперь, если Боб измерит состояние своего кубита — измерение тоже будет выглядеть случайным — но когда Алиса и Боб сообщат друг другу о результатах, они окажутся одинаковыми. Это так, потому что состояние всей системы может быть только |00> или|11>.
Запутанность также позволяет действовать одновременно нескольким состояниям - в отличие от классических битов, которые могут иметь только одно значение в каждый момент времени. Запутанность — необходимый ингредиент любого квантового вычисления, которое не может быть эффективно осуществлено классическим компьютером.
Состояние Бэлла — центральный элемент знаменитого ЭПР-парадокса: как одна частица моментально «знает» о том, что сделали со второй? Это возможно только если частицы как-то заранее договорились, какой результат измерения дать (теории скрытой переменной, Эйнштейн, ОТО), или если одна моментально, т. е. быстрее скорости света, передала информацию другой (нелокальные теории, Бор, КМ). В 1964 Бэлл показал, что предсказания квантовой теории кардинально отличаются от результатов любой теории скрытой переменной. В 1981 Аспект поставил эксперимент, который подтвердил, что скорее права КМ.
Устройство
Кубит.
Кубит — это физическая квантовая система, которая может пребывать в двух различимых состояниях (например, верхний и нижний спин электрона). Измерение состояния кубита даёт 0 или 1, как и обычного бита (измерение в квантовой механике — это целое сложное поле дебатов, зависящее от различных интерпретаций квантовой механики). Разница с битом в том, что кубит может пребывать и в суперпозиции этих двух состояний.
Отличия от бита:
- кубит содержит непрерывные комплексные значения. Но, вследствие принципа неопределённости Гейзенберга, его полное значение точно измерить невозможно.
- кубит нельзя целиком перевести в классический бит, т.е. считать или скопировать – к. состояние можно только перенести на другую физическую систему с разрушением источника, с помощью к. телепортации.
- передача информации в кубитах осуществляется через преобразования над пространством состояний, сохраняющие след.
Работа кк состоит в том, что мы устанавливаем кубиты в начальное состояние, которое отражает задачу; затем воздействуем на них конечной последовательностью квантовых логических вентилей (эта последовательность называется квантовый алгоритм); и в конце мы производим измерение - коллапсируя состояние системы в 1 из 2n базовых состояний. Результат, таким образом, даёт не более n битов информации.
Квантовые алгоритмы обычно недетерминистичны — т. е. дают ответ с некоторой вероятностью.
2) Состояния кубита:
1. чистые состояния — линейная суперпозиция базовых состояний |0> и |1>:
|ψ>=α|0>+β|1>.
где α и β — это амплитуды вероятности, комплексные числа в общем случае. При измерении состояния |ψ> - результат будет |0> с вероятностью |α2|, и |1> с вероятностью |β2|:
|α2|+|β2|=1.
Сфера Блоха: 
Это комплексная проективная прямая в Гильбертовом пространстве состояний — единичная сфера.
Классический бит может быть только на Северном или Южном полюсе сферы, в одном из базовых состояний |0> или |1>. Кубит же может быть в любой точке на поверхности сферы — это чистые состояния; или внутри неё — это смешанные состояния.
α=cos(θ/2)
β=eiφsin(θ/2)
Например, чистое состояние 1/√2|0>+i/√2|1> будет лежать на экваторе сферы, на положительной оси y.
Поверхность сферы — двумерное пространство чистых квантовых состояний. (Хоть α и β — комплексные числа — это пространство не четырёхмерно, поскольку есть 2 ограничения: |α2|+|β2|=1; и то что общая фаза состояния не имеет физического смысла — так что мы можем выбрать α вещественным)
(сфера Блоха годится только для двухуровневой системы, для больших размерностей визуализация перестаёт быть столь наглядной)
2. смешанные состояния — это статистический ансамбль чистых состояний, т. е. распределение вероятностей между всеми возможными состояниями системы. Они неизбежно возникают в составных к. системах H1 (x) H2 с запутанным состоянием в них, когда часть H2 недоступна наблюдателю. Состояние части H1 описывается как частичный след состояния H2.
Смешанное состояние описывается не кетом, а матрицей плотности (чистое состояние также можно описать матрицей плотности). 
. Это способ описать поведение множества частиц с помощью статистического формализма для одной частицы — через распределение вероятностей состояний, в которые эти частицы могут попасть.
На сфере Блоха смешанные состояния — это точки внутри сферы (это следует из переопределения оператора плотности через вектор Блоха - многабукаф). В нашем случае, они будут описываться матрицей 2x2, которая самосопряжённая (
), положительно-определённая, и имеет след=1.
В смешанном состоянии, в отличие от суперпозиции состояний, различные квантовые состояния не интерферируют между собой, так как при определении среднего складываются не волновые функции, а средние значения.
(пример: эксперимент с двумя щелями. Каждый фотон пребывает в суперпозиции состояний «правая щель»-«левая щель», в результате образуется интерференционная картина. Пучок фотонов пребывает в смешанном состоянии, т. е. каждый фотон попадает в левую ИЛИ правую щель с той или ной вероятностью)
Смешанные состояния возникают, когда наблюдатель не знает, на какое именно чистое состояние осуществляется воздействие. Также, если некоторые элементы к. системы находятся в запутанном состоянии, каждый из них должен рассматриваться как находящийся в смешанном состоянии, даже если система целиком находится в чистом состоянии.
Операции над кубитами
Измерение в стандартном базисе — получаем информацию о состоянии кубита. Результат будет|0> с вероятностью |α2|, и |1> с вероятностью |β2|. Измерение меняет значения α и β. Например, если было измерено |0>, то α меняется на 1, а β - на 0. Измерение кубита, запутанного с другой квантовой системой, переводит чистое состояние в смешанное:
Например, если мы измерим первый кубит в двухкубитной системе a|00>+b|01>+c|10>+d|11>, то получим:
С вероятностью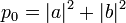 
первый кубит перейдёт в состояние 
, а второй — в состояние 
,
С вероятностью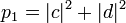 
первый кубит перейдёт в состояние 
, а второй — в состояние 
.
Т.е. измерение даст базовое состояние у первого кубита, и суперпозицию у второго. Это означает, что система оказалась в смешанном состоянии.
Измерение не является унитарным преобразованием, т. к. оно необратимо.
Работа к. комьютера заключается в инициализации начального состояния, применении последовательности к. вентилей, и затем измерении результата.
В случае классического вероятностного компьютера, мы выбираем из распределения вероятности на 2-битном регистре, и получаем одно точное значение, например 00.
В к. компьютере мы измеряем состояние двух кубитов, коллапсируя систему к классическому распределению, а затем уже вероятностно выбираем из этого распределения.
Поэтому большинство алгоритмов дают результат с некоторой вероятностью. Многократно инициализируя, прогоняя и измеряя результат, мы увеличиваем вероятность правильного ответа.
Вентили
Квантовый логический вентиль — это унитарное преобразование над пространством состояний, соответствующее вращению кубита в сфере Блоха. Вентили — унитарны (т.е. сохраняют скалярное произведение), т. к. эволюция к. системы должна сохранять норму, чтобы вероятности суммировались к 1.
Т.е. одна операция над кубитом затрагивает сразу все его возможные состояния — это и обеспечивает параллелизм вычислений.
В классическом вычислении, обратимый вентиль — это биективное отображение
f:{0,1}n->{0,1}n
Т.е. переводит n битов в n битов. Например, NOT. А AND или OR необратимы.
В к. вычислении, мы имеем Гильбертово пространство линейных суперпозиций классических последовательностей битов. Это векторное пространство над комплексными числами, размерности 2 n.
И к. вентиль отображает его на само себя. Т.е. количество входов всегда равно количеству выходов.
Наиболее широко применяемые вентили: