Определение скоростей точек и звеньев механизма

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра ОПД

 

 

 

Контрольная работа

ПО ПРИКЛАДНОЙ МЕХАНИКЕ

СамГУПС 190701. 6511.21 ПЗ

 

Исполнитель: студент Волков В.С.

Научный руководитель

ст.преподаватель___________

^{(подпись)}

 

 

Орск 2011

ЗАДАНИЕ

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

1) определить степень подвижности;

2) построить 12 положений механизма (через 30⁰ углового перемещения ведущего звена) и траектории движения обозначенных точек механизма;

3) построить план скоростей заданных точек механизма при указанном в задании угле поворота ведущего звена φ₁ относительно указанной на схеме оси.

4) построить план ускорений заданных точек механизма при указанном в задании угле поворота ведущего звена φ₁ относительно указанной на схеме оси.

Исходные данные: L _OA=80 мм, L _CD=300 мм, L _OC=100 мм, L _DE=400 мм, L _AB=250 мм, b =270 мм, =65 рад/с, =60 градус.

 

 

 

Рис.1.1Схема шестизвенного механизма

 

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

1. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА

 

Определим степень подвижности всего механизма по формуле Чебышева для плоских шарнирно-рычажных механизмов:

W = 3×n – 2P₅ – P₄ = 3×5 - 2×7 – 0 = 1,

где n – количество подвижных звеньев,

P₄ – количество кинематических пар 4-ого класса,

P₅ – количество кинематических пар 5-ого класса.

Определим кинематические пары:

0-1 низшая 5 кл. вращательная

1-2 низшая 5 кл. вращательная

2-3 низшая 5 кл. вращательная

3-0 низшая 5 кл. поступательная

1-4 низшая 5 кл. вращательная

4-5 низшая 5 кл. вращательная

5-0 низшая 5 кл. вращательная

Данная цепь является механизмом, так как степень подвижности W = 1, что соответствует числу заданных законов движения.

Разложим механизм на структурные группы Ассура. С конца механизма отсоединим группу Ассура состоящую из звеньев 4-5. Определим класс и порядок группы Ассура (2-ой класс, 2-ой порядок).

Полученную группу покажем на листе 1.

Запишем формулу строения механизма: I→II/2→II/2

Класс механизма II.

ВЫВОД: механизм кривошипно-коромысловый II-ого класса состоит из механизма 1-ого класса и одной присоединенной группы- 1 вида, 2-ого класса, 2-ого порядка

 

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

2. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИИ ДВИЖЕНИЯ ТОЧЕК, ЗВЕНЬЕВ МЕХАНИЗМА

 

Поскольку кривошип О А совершает вращательное движение, то траекторией движения точки А является окружность. Из точки О строим окружность радиусом равным длине кривошипа ОА.

Выбираем масштаб построения:

μ_v = V_a/ра=5,2/52=0,1

где V_a – скорость кривошипа, м/с;

pa – длина отрезка, изображающего кривошип на плане механизма, мм.

ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК И ЗВЕНЬЕВ МЕХАНИЗМА

 

Кинематический анализ выполняется в последовательности, предусмотренной формулой строения механизма, поэтому начинаем кинематический анализ с основного двухзвенного механизма, состоящего из кривошипа 1 и стойки 0.

Определяем скорость точки А. Поскольку точка А вращается вокруг неподвижной точки О с постоянной угловой скоростью w ₁, то

V_a=ω₁*l_OA

Вектор и направлен в сторону вращения кривошипа О А.

V_a=65*0.08=5.2 м/с

Для определения скорости точки В рассмотрим ее движение совместно со звеном 2 (шатун) и звеном 3 (коромысло).

Шатун совершает плоское движение, которое состоит из поступательного (переносного) движения вместе с точкой, параметры движения которой известны (точки А), и вращательного (относительного) движения вокруг этой точки. Следовательно:

где – линейная скорость точки В во вращательном движении относительно точки А (направлена ^А B).

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

Рассматривая движение точки В со звеном 3, запишем

где – переносная скорость точки B, принадлежащей стойке О ();

– линейная скорость точки В во вращательном движении относительно точки С ().

Полученные уравнения решим графически, путем построения плана скоростей (см. Лист 1).

Через точку p, выбранную в качестве полюса плана скоростей, проводим линию, перпендикулярную ОА, и откладываем вектор скорости точки А.

Через точку а, перпендикулярно А В, проводим прямую, представляющую собой линию действия вектора . Через полюс р, перпендикулярно ВC, проводим прямую, представляющую собой линию действия вектора . Пересечение этих прямых определяет положение точки в на плане скоростей. По правилу сложения векторов определяем направления найденных скоростей (оба вектора направлены к точке в). Измерив длины полученных векторов, получим:

Определим скорость точки D:

Откладываем на плане скоростей вектор () ( OC)

Скорость точки D:

.

Определяем мгновенные значения угловой скорости шатуна и коромысла:

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

Для определения направления угловой скорости w₂ мысленно переносим вектор линейной скорости точки B в относительном вращательном движении относительно

точки A (вектор ) с плана скоростей в точку B плана механизма. Угловая скорость шатуна ВA направлена по часовой стрелке.

Аналогично для определения направления угловой скорости w₃ мысленно переносим вектор линейной абсолютной скорости точки B (вектор ) с плана скоростей в точку B плана механизма. Угловая скорость коромысла BС направлена против часовой стрелки.

Показываем направление w₂, w₃, w₄ на плане механизма (см. лист 1).

 

4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК И ЗВЕНЬЕВ

 

Определяем ускорение точки А. Так как кривошип вращается с постоянной угловой скоростью w ₁, то

.

Вектор направлен по радиусу (по кривошипу) к центру вращения, то есть к точке О.

Для определения абсолютного ускорения точки B запишем уравнения:

,

где – полное относительное ускорение точки В в ее вращательном движении относительно точки А;

, – нормальное и тангенциальное ускорение точки В в ее относительном вращательном движении относительно точки А. Вектор направлен вдоль звена ВА от В к точке А. Вектор 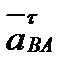направлен по линии, перпендикулярной ВА:

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

b₀– ускорение точки B, принадлежащей стойке, b₀ =0;

Таким образом, имеем систему двух векторных уравнений с двумя неизвестными (, ), которую решим графически путем построения плана ускорений (см.Лист 1).

Через произвольную точку p, принятую за полюс плана ускорений, проводим линию, параллельную О А, и на ней откладываем произвольной длины вектор , изображающий ускорение точки А. Определяем масштаб плана ускорений:

.

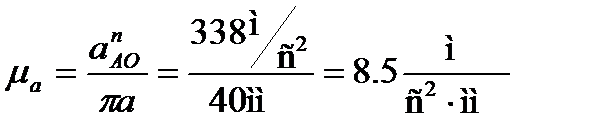Рассматриваем первое векторное уравнение для ускорения . Через точку а проводим прямую, параллельную звену ВА, и на нем, в выбранном масштабе, откладываем отрезок аb^’, изображающий на плане ускорений вектор нормального ускорения точки B при ее вращении относительно точки A ().

Модуль тангенциального ускорения точки B относительно точки A:

.

Соединив на плане ускорений точки b и a, найдем вектор, изображающий вектор полного относительного ускорения точки B относительно точки A. Он направлен от точки a к точке b.

Модуль полного относительного ускорения точки B относительно точки А:

.

Ускорение точки D шатуна находим:

где – полное относительное ускорение точки D в ее вращательном движении относительно точки E;

, – нормальное и тангенциальное ускорение точки D в ее относительном вращательном движении относительно точки E. Вектор направлен вдоль звена DE от D к точке E. Вектор направлен по линии, перпендикулярной DE:

Лист

Лист

Изм

№ документа

Подпись

Дата

СамГУПС 190701. 6511.21

Искомое значение ускорения точки D:

.

Определяем мгновенные значения угловых ускорений звеньев:

кривошип e ₁=0, так как w ₁= const;

шатун ;

коромысло .

Для определения направления углового ускорения e ₂ шатуна мысленно переносим вектор относительного тангенциального ускорения точки B относительно точки A (вектор 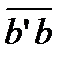) с плана ускорений в точку B плана механизма. Угловое ускорение e ₂ направлено против часовой стрелки. Аналогично находим направление углового ускорения e ₅ коромысла. Вектор относительного тангенциального ускорения точки D относительно точки E (вектор ) мысленно переносим с плана ускорений в точку D плана механизма. Угловое ускорение e ₅ направлено против часовой стрелки.

Аналогично находим направление углового ускорения e ₄ шатуна. Вектор относительного тангенциального ускорения точки D относительно точки C (вектор ) мысленно переносим с плана ускорений в точку D плана механизма. Угловое ускорение e ₄ направлено против часовой стрелки.