Так как показатель колебательности системы не задан, но известны прямые показатели качества: перерегулирование 
и время регулирования 
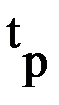,то по номограммам (приложение) находится 
, определяя его последовательно: по первой номограмме (рис. П 1.1) по заданному перерегулированию 
определяют 
(по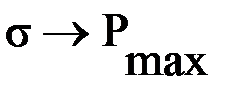 
); по найденному 
находят L и γ; а по ним 
(по третьей номограмме М (L; γ)) (рис. П 1.3) [20].
Одноконтурная структурная схема дискретного регулятора приведена на рис. 3.6 [15]. Передаточная функция объекта имеет вид (формула 3.7):
.
В системе используется фиксатор нулевого порядка (рис. 3.3). По монограммам (рис. А 1, 2) 
, 
дБ, 
, ограничение на частотный показатель колебательности 
.
Выбирается период дискретизации 
, тогда 
.
Приведенная непрерывная часть системы представляет собой последовательное включение фиксатора нулевого порядка и объекта с заданной передаточной функцией (3.10):
,
, (3.9)
Z-передаточная функция в этом случае (
) рассчитывается по формуле (3.11):
, (3.10)
Для вычисления Z-изображения выражение 
раскладывается на простые дроби:
Решая систему уравнений, находим коэффициенты:
,
.
Подставляя найденные коэффициенты, получаем выражение (3.10):
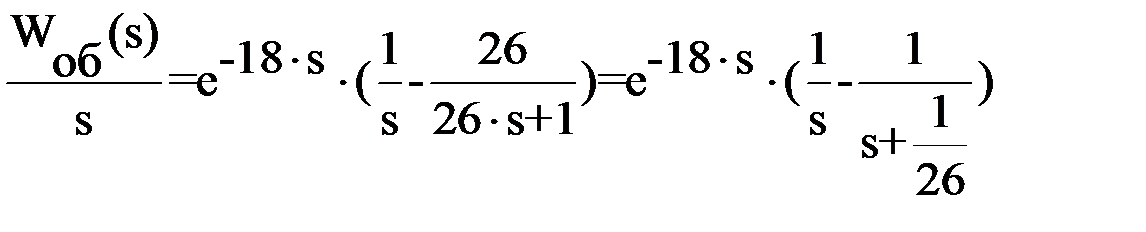, (3.11)
Так как 
, 
, где 
[18,19].
Множителю, соответствующему запаздыванию в непрерывной системе,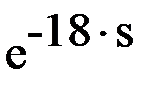 
, в Z-преобразовании соответствует множитель 
.
Тогда:
,
.
Тогда:
, (3.12)
Z-передаточная функция приведенной непрерывной части с учетом фиксатора нулевого порядка:
. (3.13)
Передаточная функция дискретного ПИ-регулятора:
,
, (3.14)
Передаточная функция разомкнутой системы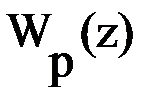 
:
(3.15)
Заменяя 
, получаем комплексную частотную характеристику (КЧХ) или амплитудно-фазовую частотную характеристику разомкнутой системы (АФЧХ):
,(3.16)
Т.к. 
, то частоту при построении КЧХ можно изменять в пределах 
или 
.
Выбирается наибольшая постоянная времени объекта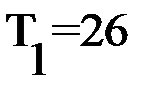 
и определяется интервал варьирования постоянной интегрирования 
.
Строится окружность, соответствующая 
, 
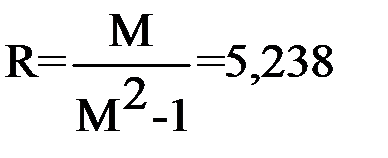; координаты центра О 
.
Задается значение 
с, строится КЧХ, например для 
. КЧХ пересекает окружность, уменьшаем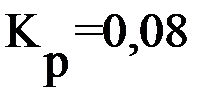 
- КЧХ не касается окружности и т.д.. Результаты сводятся в табл. 3.4, по ним строится график зависимости 
от 
(рис. 3.4). М-файл для расчета представлен в приложении 2.
Таблица 3.4
Значения настроек ПИ-регулятора
|
| 
|
|
| 0,310 | 0,0238 | |
| 0,381 | 0,0254 | |
| 0,462 | 0,0272 | |
| 0,550 | 0,0289 | |
| 0,645 | 0,0307 | |
| 0,745 | 0,0324 | |
| 0,823 | 0,0329 | |
| 0,900 | 0,0333 | |
| 0,953 | 0,0329 | |
| 0.945 | 0,0305 | |
| 0,997 | 0,0302 | |
| 1,030 | 0,0294 | |
| 1,070 | 0,0289 | |
| 1,090 | 0,0279 |
Рис. 3.4. График зависимости Кр /Tи от Tи
Согласно полученным значениям и графику (рис. 3.4), наиболее оптимальными настройками будут 
, 
.
Для того чтобы убедиться в оптимальности полученных настроек, нужно рассчитать прямые и косвенные показатели качества, поэтому строится передаточная функция (3.18) замкнутой системы:
(3.17)
Преобразовав передаточную функцию (3.18), получим:
Косвенные показатели качества определяются по АЧХ замкнутой системы (рис. 3.5).
Рис. 3.5. Амплитудно–частотная характеристика замкнутой системы при настройках ПИ-регулятора при 
, 
Фактическое значение частотного показателя колебательности 
< 
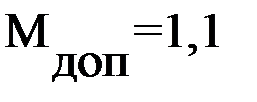, то есть расчет можно считать удовлетворительным.
Прямые показатели качества ПИ-регулятора определяются по переходной характеристике замкнутой системы (рис. 3.6).
Рис. 3.6. График переходной характеристики замкнутой системы при настройках ПИ-регулятора 
, 
Прямые показатели качества:
- перерегулирование 
< 
;
- время регулирования 
с < 
.
Так как полученные показатели качества управления меньше допустимых, настройки ПИ-регулятора можно считать оптимальными.
Выводы по разделу
- осуществлен теплотехнический расчет трубопровода, расположенного на УПСВ – 7 Уренгойского месторождения;
- выбран тип регулятора температуры;
- произведен расчет оптимальных настроек регулятора температуры.