М. Преображенский
Финансовая астрология, Фибоначчи и кое-что ещё...
Идея данного мини-исследования появилась пару лет назад, в период изучения мною концепций известного финансового аналитика Вильяма ДелбертаГанна. Считается, что их автор, легендарный трейдер и астролог, разработал свои уникальные техники на основе тайного древнего знания, и что многое специально было им запутано или зашифровано с целью затруднить понимание «праздно интересующейся публики». На самом деле все его работы тесным образом связаны с астрологией, которую большинство «серьезных» экономистов и аналитиков рынка предпочитает осуждать, а не изучать. Однако любой, имеющий отношение к рынкам и одновременно вооруженный астрологическим знанием, не может не восхититься возможностями, которые предоставляют в деле прогнозирования цен многочисленные техники Ганна.
Настоящая работа не предполагает детального знакомства со всеми положениями его теории; ее цель – исследовать, существует ли взаимосвязь между «волнами Эллиота», числами Фибоначчи и работами Ганна с точки зрения астрологии. Однажды увидев эту связь, уже невозможно утверждать, что астрология – лженаука, не имеющая практического применения.
Проверка идеи заняла в свое время не более 15-минут и уместилась на половине одного листа. Однако «законы жанра» при обнародовании любого исследования диктуют необходимость некоторого описания, пусть и поверхностного, предпосылок гипотезы. Те, кто знаком с ними, могут сразу перейти к последней части и выводам, которые для самого автора оказались несколько неожиданными.
Теория Эллиота
Графики цен любого рынка состоят из чередующихся отрезков движения цен вверх или вниз. Если рассмотреть любой такой отрезок внимательнее, то становится заметным, что он образует в развитии фигуру из пяти волн. Три из них совершают движение в направлении основной тенденции и разделяются двумя откатами - волнами противоположного направления (Рис. 1). Каждая такая пятиволновка находится внутри структуры более высокого порядка. Пятиволновая модель является основной фигурой, и все остальные модели состоят из нее.
Согласно теории Р.Н. Эллиотта, полный цикл развития движения цен происходит в соответствии со строго повторяющимся ритмом или моделью: пять волн вверх и три волны вниз (см. Рис.2). Полный цикл, состоящий из восьми волн можно представить двумя противонаправленными фазами: движущей, или импульсной, называемой «пятеркой», и корректирующей, называемой «тройкой»

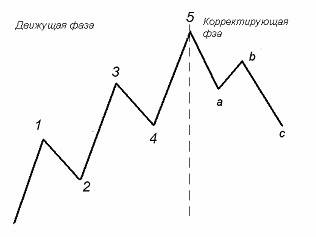
Рис 1. Модель пятиволнового цикла Рис.2. Модель полного 8-волнового цикла
Каждая 8-волновая структура находится, как в матрешке, внутри такой же структуры более высокого волнового порядка. Идеализированное поведение рыночных цен изображено на Рис. 3. Одна и та же модель проявляется в графиках любых временных интервалов – от пятиминуток до годовых. На Рис.4 показано два линейных графика: пятнадцатиминутный USD/JPY от 25.08.2004г. (слева); и помесячный GBP/USD с января 2001 г. по ноябрь2004 г. (справа). Оба они образуют очень похожие формы, несмотря на колоссальное различие во временном масштабе.

Рисунок 3. Идеализированная структура рынка.


Рис. 4. Повторение структуры рынка в разных временных масштабах.
Закон волн было бы легко применять, если бы он мог полностью описывать поведение рынка, однако в реальности существует множество разновидностей подволн, форма и последовательность которых искажает идеальную картину. Эллиотом и его последователями такие разновидности описаны и классифицированы в многочисленных работах, которые здесь, естественно, рассматриваться не будут. Нас интересует другое.
Вернемся к идеальной структуре и подсчитаем количество подволн в каждом цикле, начиная с самого большого уровня и уровнями ниже.
Самый высокий уровень 1 + 1 = 2
Уровнем ниже 5 + 3 = 8
Следующий уровень вниз 21 + 13 = 34
Следующий уровень вниз 89 + 55 = 144
Первое, что бросается в глаза – количество волн при дроблении структуры рынка от более высокого уровня к более глубокому выражается числами, образующими последовательность Фибоначчи.
Вселенная Фибоначчи
Последовательность чисел Фибоначчи была открыта (на самом деле, повторно) Леонардо Фибоначчи де Пиза, математиком тринадцатого века. Когда Эллиотт описывал свою теорию, он, в частности, ссылался на последовательность Фибоначчи, как математическую основу Закона волн. То есть, фондовый рынок по динамике цен и развертыванию во времени имеет склонность демонстрировать соотношения, сопоставимые с последовательностью Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…, где сумма любых чисел, расположенных рядом, дает следующее число. После первых нескольких чисел отношение любого числа к следующему старшему равно примерно 0.618 к 1, а к соседнему младшему - приблизительно 1.618 к 1. Чем дальше вдоль последовательности, тем ближе отношение приближается к фи, которое является иррациональным числом 0.618034… Соотношение между числами, расположенными через одно в последовательности, приблизительно равно 0.382, что является инверсией от 2.618 (1:2.618).
Указанная выше последовательность чисел не является единственно возможной. Для образования подобного ряда можно взять любые два положительных числа. Любая последовательность Фибоначчи обладает, кроме прочих, одним важным свойством: соотношение Фи становится очевидным на ВОСЬМОЙ (!) ступени построения ряда.
Фи является единственным числом, которое после сложения с 1 дает свою же инверсию: 0.618+1=1:0.618.
1.618 (или 0.618) известно как Золотая пропорция или Золотое сечение. Его гармония приятна для глаз и является важным явлением в музыке, искусстве, архитектуре и биологии. Природа использует Золотое сечение повсеместно: от таких мелких форм, как атомные структуры, микрокапиллярымозга и молекулы ДНК до таких огромных, как планетарные орбиты и галактики. Оно проявляется в таких разнообразных явлениях, как расположение квазикристаллов, планетарных расстояний и периодов обращения планет, мозг и нервная система, музыкальная аранжировка и строение растений и животных. Человеческое тело является воплощением Золотых сечений во всем - от внешних размеров до устройства лица.
Произведения в искусстве значительно улучшены с использованием Золотого прямоугольника, стороны которого находятся в пропорции 1.618 к 1. Культ его ценности и использования был особенно сильным в древнем Египте и Греции и во времена Ренессанса, т.е. во всех важных периодах цивилизации. Леонардо да Винчи придавал огромное значение Золотой пропорции. Он также находил ее приятной в своих соотношениях и говорил: "Если предмет не имеет правильного облика, он не работает". Многие из его картин обладают правильным обликом, потому что он использовал Золотое сечение для того, чтобы усилить их привлекательность.


Рис 5. Построение Золотой спирали.
Золотое сечение и Золотой прямоугольник представляют статические формы как естественной, так и сотворенной человеком красоты и деятельности. Проявление естественного динамизма, организованного движения, роста и развития может быть символизировано Золотой спиралью. Любой Золотой прямоугольник, как показано на Рис. 5, можно разделить на квадрат и меньший Золотой прямоугольник. Этот процесс теоретически можно продолжать до бесконечности. Получающиеся прямоугольники скручиваются внутрь, а пунктирные линии, которые сами находятся в золотом соотношении одна к другой, рассекают прямоугольники по диагонали и точно обозначают теоретический центр скручивающихся квадратов. Приблизительно из центральной точки мы можем начертить спираль, соединяя точки пересечения каждого скручивающегося квадрата в порядке возрастания размера. В любой точке развития Золотой спирали, отношение длины дуги к ее диаметру равно 1.618. Диаметр и радиус в свою очередь соотносятся с диаметром и радиусом, отстоящих на угол в 90 градусов, с коэффициентом 1.618, как показано на Рис. 6.

Рис.6. Соотношение радиусов дуг, составляющих «золотую спираль»
Идеализированная концепция Эллиота показывает, что фондовый рынок обладает точно такой же математической основой, как и природные явления. На Рис.7 показано, что структура волнового развития рынка также может быть основой для построения Золотой спирали.

Рис. 7. Структура рынка как основа построения для «золотой спирали»
В.Д. ГАНН и Великий Квадрат
Помимо теории Эллиота и чисел Фибоначчи существует еще работы В.Д Ганна, описывающие динамику рынка и взаимосвязь цен со временем.
Возьмем одну из самых популярных и наиболее распространенных ганновских техник – «Квадрат-калькулятор цен» (см. рис. 8 и 9), или «квадрат Ганна». На самом деле Ганн не является изобретателем самого Квадрата, который получил такое название благодаря его применению Ганном для описания движений цен на финансовых рынках. Сам Квадрат является инструментом гораздо более древнего знания, корни которого уходят во времена египетских жрецов, а может быть, и еще глубже.
Квадрат Ганна представляет собой расположение ряда простых чисел по принципу спирали, в центре которой находится единица. Ряд чисел можно раскручивать до бесконечности, мы же ограничимся числом 361, что почти точно соответствует количеству градусов в круге. Если расположить числа по кругу, то его можно разделить на 8 равных секторов по 45º. В прямоугольном виде мы будем иметь 4 оси – две диагонали и две в виде креста, разделяющего Квадрат на 4 части. По одной из диагоналей располагаются квадраты простых чисел: 4, 9, 16, 25, 36, 49, 64, …, 361, …
Ганн обнаружил удивительную закономерность, позволяющую довольно точно находить точки поворота рынка: числа, которые лежат на осях Квадрата, соответствуют рыночным уровням сопротивления и поддержки в значениях цен, а по времени – точкам поворота рынка. Кроме того, значения цен, равные квадратам простых чисел, возникают в моменты времени, также соответствующим квадратам простых чисел. Это справедливо для любой взятой за основу единице времени – час, 4 часа, день, месяц, год…
Итак, выделено три факта, имеющих важное значение для описания рыночных процессов: волны Эллиота, последовательность Фибоначчи и квадраты простых чисел.
На взаимосвязь первых двух указывалось выше. А как насчет третьей – есть ли что-либо, объединяющее ее с остальными?
Чтобы разобраться, возьмем за единицу времени, например, день и построим две календарные диаграммы (См. Диаграммы 1 и 2). На одной отметим квадраты простых чисел и числа Фибоначчи для рабочих, на другой – для календарных дней и отметим совпадения. Допуск на такие совпадения возьмем не более 1-го дня. Одновременно на каждой диаграмме отметим аспекты (угловые расстояния между Солнцем и Луной) солнечно-лунного цикла, повторяющегося примерно через 29-30 календарных дней.
Переложение диаграмм на Квадрат Ганна (Рис.8 и Рис.9) позволяет нагляднее выделить совпадения в обоих способах.
Диаграмма 1. Совпадение квадратов чисел для рабочих дней и номеров календарных дней, соответствующих числам Фибоначчи

Диаграмма 2. Совпадение квадратов чисел для календарных дней и номеров рабочих дней, соответствующих числам Фибоначчи

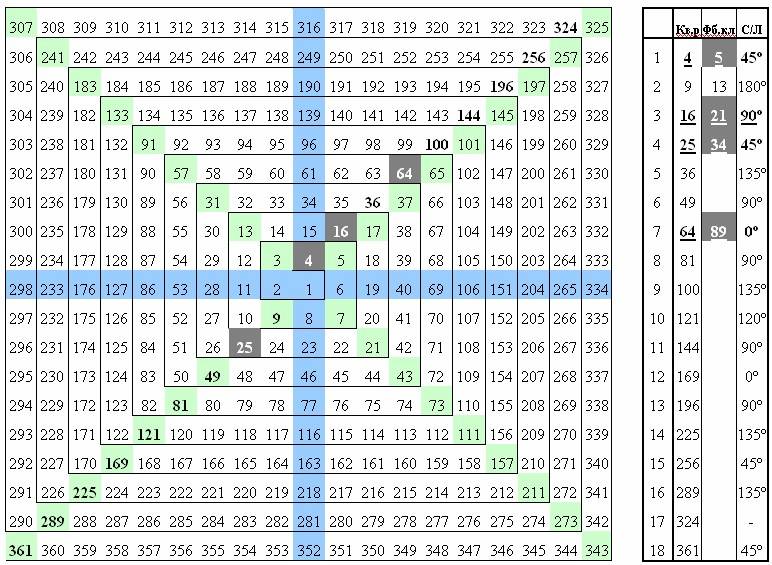
Рис. 8. Квадрат Ганна из рабочих дней. Совпадение квадратов чисел и номеров календарных дней, соответствующих числам Фибоначчи.
В таблице справа:
Кв.р. – номера рабочих дней от начала цикла, совпадающие с квадратами простых чисел;
Фб.кл. – номера календарных дней от начала цикла, совпадающие с числами Фибоначчи;
С/Л – аспект в солнечно-лунном цикле, наиболее близкий по времени к моменту совпадения;

Рис. 9. Квадрат Ганна из календарных дней. Совпадение квадратов чисел и номеров рабочих дней, соответствующих числам Фибоначчи.
В таблице справа:
Кв.к. – номера календарных дней от начала цикла, совпадающие с квадратами простых чисел;
Фб.р. – номера рабочих дней от начала цикла, совпадающие с числами Фибоначчи;
С/Л – аспект в солнечно-лунном цикле, наиболее близкий по времени к моменту совпадения
При анализе Диаграмм 1, 2 и рисунков 8 и 9 находим, что есть 8(!) важных совпадений:
- четыре рабочих дня, соответствующих квадратам простых чисел – 4, 9, 16, 25, 64 – совпадают с четырьмя календарными днями, имеющими номера, соответствующие числам Фибоначчи – 5,13, 21, 34, 89;
- четыре рабочих дня, соответствующие числам Фибоначчи - 5, 8, 13, 233 - совпадают с тремя календарными днями – квадратами простых чисел - 4, 9, 16, 324
Результаты обобщены в таблице 1:

Кроме этого:
- рабочие дни с порядковыми номерами, равными квадратам простых чисел, практически все совпадают с днями, когда аспекты Между Солнцем и Луной кратны 45º - ОДНОЙ ВОСЬМОЙ КРУГА - 0º, 45º, 90º, 135º 180º;
- в рабочие дни с порядковыми номерами чисел Фибоначчи, совпадающие с календарными днями, имеющими порядковые номера квадратов чисел, наблюдаются аспекты, кратные 60º - 0º, 60º, 120º, 180º;
Можно было бы построить календарные диаграммы, где отсчет рабочих дней начинается не с условного понедельника, а, скажем, со среды. При этом совпадения смещаются, но и в этих случаях наблюдаются сходные закономерности.
Один день в качестве единицы времени был выбран для большей наглядности. Можно взять любой другой шаг– три дня, час, месяц и т.д., - и везде будут наблюдаться корреляции с астрологическими паттернами.
Из всего изложенного можно сделать очевидный вывод: