Описание положения и движения МТ в системе отсчета.

Классическая механика. Лекция 1. Кинематика

 

1. Кинематика – это раздел механики, в котором изучаются способы математического описания движения тел. При этом причины движения не рассматриваются.

2. Система отсчета. Движение тела изучается в системе отсчета. Система отсчета состоит из трех обязательных компонентов:

2.1. Тело отсчета, относительно которого можно наблюдать и изучать движение тела

и инструментов для измерения движения тела:

2.2. Система координат, связанная с телом отсчета

Часы

3. Единицs измерения. Для измерения положения точки изучаемого тела в системе отсчета используются единицы длины и времени:

3.1. Эталон длины, называемый метр. Исторически за 1м принята длине парижского меридиана, деленная на 40 000 000. Современное определение метра базируется на мировой константе – скорости света. Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды.

3.2. Для измерения времени между событиями, используется эталон времени – секунда. 1 секунда ранее определялась, как 1/86400 часть суток. Современное определение: Секунда — время, равное 9 192 631 770 периодам одного из видов излучения атома цезия-133.

4. Виды тел и движений, которые они совершают:

4.1. Самые сложные движения могут совершать деформируемые тела. Тело называется деформируемым, если расстояние между какими – либо его двумя точками могут изменяться во времени. Такие тела могут и совершать движения, как единое тело и его части могут двигаться друг относительно друга. Вообще говоря, все тела могут деформироваться, в той или иной степени.

4.2. Поэтому рассмотрим более простую модель тела– абсолютно твердое тело. Оно не может деформироваться. Простейшие формы движения такого тела – это поступательное и вращательное.

4.2.1. Поступательным называется движение, при котором все точки тела двигаются по одинаковым траекториям.

4.2.2. Вращательным называется движение тела, при котором у тела имеется ось вращения, т.е. прямая, все точки которой неподвижны. Все остальные точки тела движутся по окружностям, лежащим в плоскости перпендикулярной оси вращения и имеющим центр на этой оси. Сама ось неподвижна. Впрочем, возможно движение, когда ось вращения изменяет свое положение, но этот сложный вариант в школе не рассматривается.

4.2.3. Существует особый вид неравномерного движения – колебательное. Тело колеблется, если оно совершает движения, которые повторяются через некоторые промежутки времени. Если эти промежутки одинаковые, то такие колебания называются периодическими. Колебательное движение может состоять и из поступательных и из вращательных движений.

4.3. Материальная точка (сокращенно МТ), простейшая модель тела – это тело, размерами которого в данной модели или в задаче можно пренебречь. Также тело можно рассматривать, как МТ в случае поступательного движения абсолютно твердого тела, т.к. при этом движении все точки тела двигаются по одинаковым траекториям.

Описание положения и движения МТ в системе отсчета.

5.1. Положение МТ в системе отсчета определяется посредством системы координат, связанной с телом отсчета. Существуют различные системы координат. В данном курсе физики будет использоваться две: декартова и полярная. Вид и размещение системы координат выбираются произвольно, исходя из удобства в конкретной задаче.

В декартовой системе координат положение точки в пространстве определяется тремя числами – проекциями этой точки на оси координат. Если движение МТ происходит в плоскости, то достаточно двух координат, а если по прямой, то достаточно и одной.

Полярная система координат будет рассмотрена позже при изучении движения МТ по окружности.

5.2. Движение МТ.

5.2.1. Траектория движения -- это линия, вдоль которой движется МТ.

5.2.2. Путь L – это длина траектории от начала движения до его конца. Причем если точка движется сначала вперед, а потом по той же траектории назад, то пути вперед и назад складываются. Таким образом, путь всегда L >0, т.е. это вещественное положительное число.

5.2.3. Среднепутевая скорость. Ее обычно называют просто средней скоростью. Это отношение пути L, пройденного МТ ко времени Δt, которое на это было потрачено. V_ср = L / Δt.

Размерность скорости [V] = м/с. Единица измерения скорости 1 м/с.

Полезно запомнить, что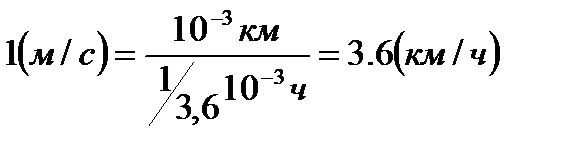

5.2.4. Перемещение МТ - это направленный отрезок, соединяющий начальную и конечную точку движения МТ.Величина, которая характеризуется не только числовым значением, но и направлением, называется вектор. Здесь векторная величина будет обозначаться буквой, выделеннаяжирным шрифтом. Обычно вектор обозначается стрелкой над буквой.

Перемещение – это вектор S, соединяющий начальную (1) и конечную (2) точку движения. Модуль перемещения | S | - это длина вектора. Она измеряется в метрах. Проекция вектора на ось координат S_x – это число, равное разнице между проекцией конца вектора 2_х и проекцией начала 1_х:

S_x = 2_x – 1_x и S_y = 2_y – 1_y.

Проекции S_x и S_{y –}скаляры. Модуль вектора, может быть вычислен по его проекциям по теореме Пифагора: 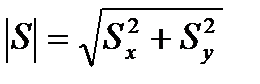, угол наклона S к оси Х может быть вычислен через тангенс угла: tg α = S_y /S_x

5.2.5. Мгновенная скорость. Пусть МТ за время Δt перемесилась из точки 1 в точку 2 по некоторой траектории, совершив перемещение Δ S. Перемещение, совершенное МТ в единицу времени V _ср = Δ S /Δt называется средней скоростью. Скорость – это вектор, направленный так же, как перемещение. Единица измерения скорости 1 м/с. Если мы устремим время измерения к нулю Δt →0, то точка 2 устремиться к точке 1, а вектор V станет касательной к траектории в точке 1, а его модуль | V _ср­|→ V. Полученный таким образом вектор V называется мгновенной скоростью МТ

Мгновенная скорость – это вектор, показывающий направление перемещения, и его величину в единицу времени. Вектор скорости – функция времени: V = V (t). Скорость может изменяться, как по величине, так и по направлению.

Действия над векторами

6.1. Равенство векторов. Два вектора считаются равными, если равны их длины (модули), они параллельны друг другу и стрелки направлены в одну сторону. Таким образом, если вектор переместить параллельно самому себе, то новый вектор будет равен старому.

6.2. Сложение векторов. Пусть МТ совершит последовательно два перемещения: S ₁ и S ₂. Результатом этих перемещений будет направленный отрезок S ₃, который получится, если начало второго отрезка приложить к концу первого. Это способ сложения перемещений является иллюстрацией общего правила сложения векторов, так называемого правила треугольника: S₃ = S₁ + S₂

6.3. Умножение вектора на число. Если вектор А умножить на число k, то получится вектор В = k A. Направление В совпадает с направлением А. Стрелка направлена в ту же сторону, что и у вектора А, если k > 0 и в противоположную, если k < 0. Модуль вектора | B | = k | A |. В частности, (– А) или (-1) А – это такой же вектор, но направленный в противоположную сторону

7. Построение графиков зависимости параметров движения от времени. График траектории в осях X,Y не дает полного представления о движении, поскольку на нем не видно время. Чтобы увидеть полную картину движения, нужно строить зависимости от времени таких параметров, как координата, перемещение, путь, скорость и ускорение.

Все такие графики будем строить методом последовательных приближений. Пусть исходная функция x = f(t) и ее график проходит через точку x=0 и t=0.

Если нам нужно построить график функции проходящий через точку x = x₀ и t=0, то это будет функция x= f(t) + x₀, и ее график надо сдвинуть на x₀ вдоль оси X.

Если нам нужно построить график функции, проходящий через точку x=x₀ и t= t₀, то это будет функция x= f(t – t₀) + x₀­, и ее график надо сдвинуть на величину t₀ вдоль оси t.

8. Уравнение движения. Зависимость координаты точки от времени x(t) называется уравнением движения. Пусть график уравнения движения – это кривая в осях (X,t). Построим касательную к этой кривой в точке А_0. Для этого проведем секущую через точку А₀ и другую, близкую к ней точку А, а затем устремим точку А к точке А₀. Секущая будет поворачиваться, пока в пределе не станет касательной. Как видно из рисунка tg угла наклона касательной к оси t равен: tg ϕ = Δх / Δt. а это в свою очередь мгновенная скорость в точке А₀.: tg ϕ = V, таким образом угол наклона касательной к графику перемещения тела, определяет его скорость.

9. Определение перемещения тела по графику скорости.

Пусть тело движется с переменной скоростью, график которой изображен на рисунке. Разобьем интервал времени движения тела на маленькие кусочки Δt_i и построим на каждом таком интервале прямоугольник, высота которого примерно равна значению скорости на этом интервале V(t). Будем считать, что на маленьком интервале Δt_i скорость постоянна. Тогда перемещение, совершенное на этом интервале, равно ΔS_i= V(t) Δt_i. С другой стороны, V(t) Δt_i = ΔF_i – площади этого прямоугольника. Тогда сумма площадей этих прямоугольников равна перемещению за весь интервал времени. И если Δt_i →0, а число интервалов → ∞, то сумма этих площадей будет стремиться к площади под кривой графика скорости. Таким образом перемещение тела за время Δt равно площади под графиком его скорости за это время.

10. Прямолинейное движение – это простейшая модель движения МТ, когда ее траектория – прямая линия. Поскольку систему координат можно располагать любым удобным для описания движения способом, то направим ось Х вдоль траектории движения. Тогда движение описывается, как изменение единственной координаты Х. Перемещение вдоль осей Y и Z отсутствует, т.е. S_y = S_z = 0, а S_x = Δх = х –х₀, где х и х₀ – конечное и начальное положения МТ. Отметим, что вектор перемещения в одномерном случае можно рассматривать и как вектор, и как скаляр, т.к. существуют только два возможных направления S – вдоль оси Х и против оси Х. Это соответствует знаку скаляра S > 0 или S < 0.

10.1. Прямолинейное равномерное движение. Если за любые равные промежутки времени МТ совершает одинаковые перемещения, то такое движение называется равномерным. Т.е. при прямолинейном равномерном движении V_x = Δх/Δt = const и скорость не изменяется ни по величине, ни по направлению.

При прямолинейном движении скорость, также, как и перемещение можно считать и скаляром, и вектором. Если вектор V₁ направлен против оси Х, то V_1x< 0, если вдоль оси Х, то V_2x> 0

Для прямолинейного равномерного движения (сокращенно ПРД) уравнение движения можно получить из определения скорости: V_x = Δx/ Δt = (x – x₀) /(t – t₀). Поскольку в данном случае S_y = S_z = 0, то и V_y = V_z =0, можно обозначить V_x, как V. Тогда уравнение движения будет иметь вид: x = x₀ + V (t - t₀).Если t₀ =0, тоx = x₀ + V t. Уравнение для перемещения: S = x – x₀ = Vt

10.2. Построение графиков ПРД.

Построим сначала график зависимости скорости от времени. Поскольку при ПРД V-const, то графиком будет прямая линия, параллельная оси X.

Построим теперь график перемещения при ПРД. Исходная функция будет x = Vt. Ее график – это прямая, проходящая через точку (0,0). Тангенс угла наклона tg α графика уравнения движения равен Δх/Δt = V скорости в данный момент времени. Если V > 0, то прямая идет снизу вверх, а если V < 0, то сверху вниз. Если начальное положение тела в точке t₀, x₀, то ее уравнение, как было показано в п.6 имеет вид: x = x₀ + V(t – t₀). В самом деле, при t = t₀, → х = х₀

11. Принцип независимости перемещений. Если точки участвует одновременно в нескольких перемещениях, то результирующее перемещение представляет собой векторную сумму этих перемещений: S (t) = S ₁(t) + S ₂(t) + S ₃(t) …. Иначе говоря, перемещения не зависят друг от друга. Это так называемый принцип суперпозиции (наложения), который справедлив для многих явлений физики, например, для описания результата взаимодействий тела с несколькими другими телами.

Функции S_x (t) и S_y (t) не зависят друг от друга. Т.е. может быть, что вдоль оси Y МТ вообще не двигается, т.е. S_y (t) = 0, или вдоль ось X тело движется равномерно, а вдоль Y – ускоренно.

Этот же принцип справедлив и для скорости тела, участвующего одновременно в нескольких движениях. Если равенство S (t) = S ₁(t) + S ₂(t) разделить на Δt, то получим: V (t) = V ₁(t) + V ₂(t).

Используя принцип независимости перемещений найдем формулу для расчета скорости тела при переходе из одной системы отсчета в другую. Предположим, что МТ в некоторой системе отсчета X′Y′ имеет скорость V ′. Назовем эту систему отсчета «собственной». Пусть собственная система отсчета сама движется в некоторой другой «лабораторной» системе отсчета, которую будем условно считать неподвижной, со скоростью V ₀. Пусть тело совершит за время Δt перемещение S ′ в собственной системе отсчета, а собственная система отсчета за то же время совершит перемещение S₀ в лабораторной системе отсчета. Поскольку эти перемещения независимы, можно утверждать, что тело совершит в лабораторной системе отсчета перемещение S = S ′ + S ₀. Разделив это равенство на Δt получим V = V ′ + V _0.. Это правило сложения скоростей, которое формулируется так:

«Скорость тела в неподвижной системе отсчета равна векторной сумме его скорости в движущейся системе отсчета плюс скорость движущейся системы отсчета относительно неподвижной ».

12. Равноускоренное прямолинейное движение МТ.

12.1. Ускорение. Пусть вектор скорости V за время Δt изменится на величину Δ V. Δ V – это тоже вектор. Причем вектор Δ V может быть направлен, как вдоль вектора V так и под любым углом к нему. Вектор a_ср = Δ V /Δt называется средним ускорением тела. Если Δt→0, то среднее ускорение стремиться к мгновенному ускорению a_ср → a. Чтобы понять смысл вектора ускорения разложим его на две составляющие: одна a _τ – вдоль касательной к траектории, а значит и вдоль вектора V; другая – перпендикулярно касательной a _n. Вектор a _τ, называется тангенциальным ускорением. Он показывает, как изменяется модуль вектора V в единицу времени. Вектор a _n называется нормальным или центростремительным ускорением. Он показывает, как изменяется направление вектора V в единицу времени. Размерность ускорения [м/c²], единица измерения ускорения 1 м/с² или, как говорят один метр в секунду за секунду.

12.2. Уравнения прямолинейного равноускоренного движения. Траектория движения – прямая линия, значит, положение МТ задается одной координатой Х. Равнопеременное – значит ускорение постоянно a(t) = const. Т.к. движение прямолинейное, то ускорение направлено вдоль траектории – оси Х и его можно считать скаляром. Поскольку a = ΔV/Δt, то V-V₀ = a Δt и, считая, что t₀=0, получим уравнение для скорости V(t) = V₀ +at. Поскольку а – скаляр то он может быть, как a>0, так и a<0. Соответственно, движение при этом будет или равноускоренным или равнозамедленным.

Зависимость координаты МТ от времени найдем с помощью графика функции V(t). Как было сказано выше площадь под этим графиком равна перемещению ΔF =Δх. Фигура под графиком – трапеция. Ее площадь F= Δx = Δt (V₂ + V₁)/ 2, где Δt = t₂ –t_1. Будем считать, что t₁ =0, а t₂ заменим на t. Тогда: V₂ =V₁ +at, и уравнение равнопеременного движения примет вид: x(t) = x₀ + V₀t + at²/2. Уравнение для перемещения S = x – x₀ = V₀t + at²/2

12.2.1. Построим график уравнения движения x(t) = x₀ + V₀t + at²/2. Понятно, что это парабола. Если a>0, то ветви параболы направлены вверх, а если a<0, то вниз. Координаты вершины параболы (t_m, x_m), найдем следующим образом. В вершине параболы касательная к ее графику горизонтальна, значит скорость в этой точке =0. Т.е. V = V₀ + at_m =0. Отсюда t_m = - V₀ /a. Подставим это t_m в уравнение движения. Получим x_m = - V₀²/2a +x₀. Поскольку x_m – это смещение графика параболы вверх, а t_m – смещение графика параболы вправо, то уравнение параболы будет иметь вид: x = a/2(t - t_m)² + x_m. Найдем в осях координат точку t_m, x_m и построим параболу x = at² / 2 с вершиной в этой точке (см. рис ниже).

12.2.2. 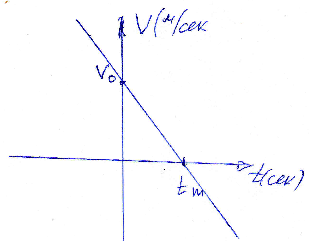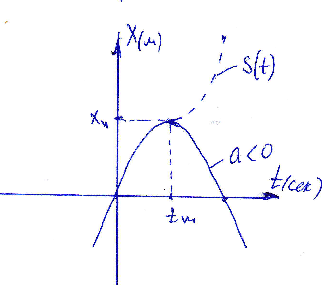Рассмотрим случай равнозамедленного движения a<0 на примере движения тела, брошенного вертикально вверх. Под действием силы тяжести любое тела на поверхности Земли движется с ускорением, направленным вниз и равным g =9,81 м/с² (примерно 10 м/с²⁾. Направим ось координат X вверх. Тогда проекция ускорения тела на ось Х равна a= - g. Пусть тело имеет в точке х=0 начальную скорость V₀, направленную вверх. Скорость V изменяется от V₀ при t=0 до нуля в точке максимального подъема (t_m, x_m), а затем изменяет знак и начинает по модулю расти. Из симметрии параболы понятно, что в точке 2t_m тело падает на землю: x=0. Уравнение для скорости при равноускоренном движении имеет вид имеет вид): V = V₀ + at. Но поскольку а = - g, то V = V₀ – gt. Уравнение движения в общем виде x(t) = x₀ + V₀t + at²/2 для данного случая приобретает вид: x = V₀ t – gt²/2. Время подъема – это время достижения точки, где V = 0. Т.е. t_m = V₀/g. Максимальная высота подъема x_m = V₀²/2g. Для построения графика движения находим точку t_m, x_m и строим параболу x= - gt²/2 с вершиной в этой точке.

Следует обратить внимание на разницу между перемещением и путем. Модуль перемещения равен пути при прямолинейном однонаправленным движении. Как только направление движения меняется приращение перемещения меняет знак, а приращение пути остается положительным.

12.2.3. Формула, связывающая начальную и конечную скорость равнопеременного движения с путем и ускорением. Для этого исключим время из системы уравнений: V_k= V_н +at и x = x₀ + V_нt + at²/2, где V_н - начальная, а V_k – конечная скорость движения Для этого выразим t из первого уравнения t= (V – V₀) /a и подставим его во второе уравнение. Получим очень полезную для решения задач формулу V_к² – V_н² = 2a (x – x₀) = 2aS, где S – перемещение.

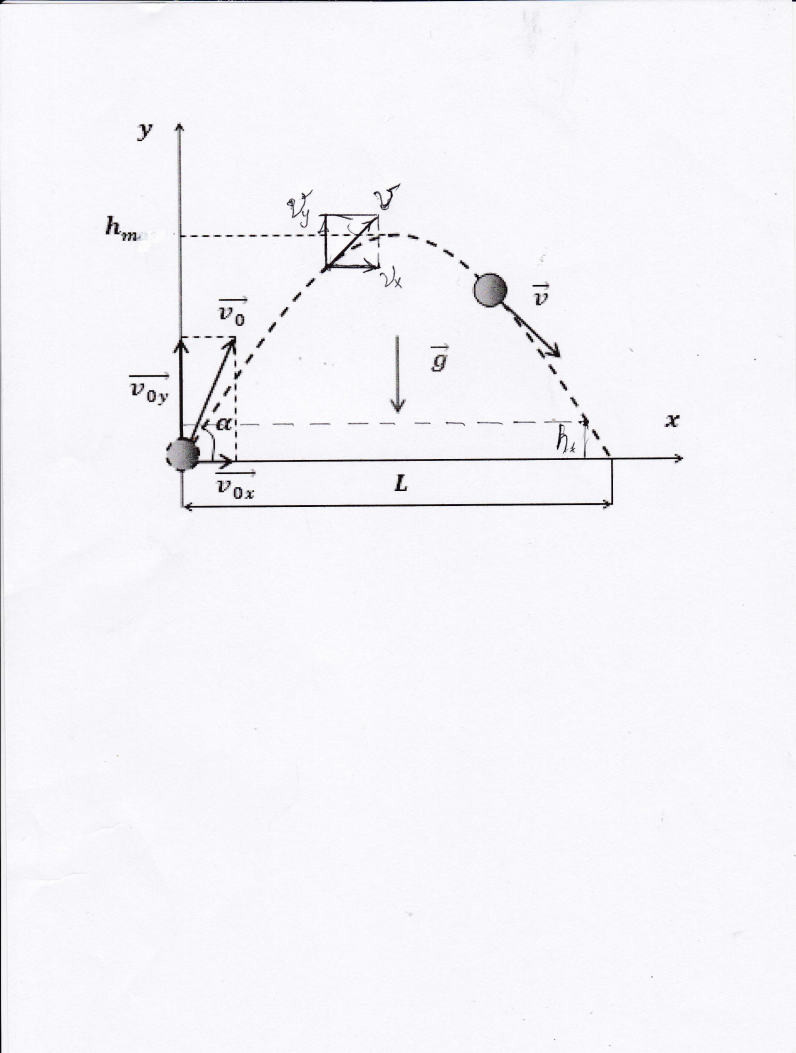
13. Движение тела, брошенного под углом к горизонту. Согласно принципа независимости движений, движение тела под углом к горизонту можно рассматривать, как два независимых движения:

1. Прямолинейное равномерное движение вдоль оси Х. Поскольку вектор ускорения g направлен вдоль оси Y, то движение вдоль оси Х происходит с постоянной скоростью

2. Прямолинейное равноускоренное движение вдоль оси Y с ускорением g.

Начальные скорости обоих движений можно вычислить, как

V_0x = V₀ cos α и V_0y = V₀ sin α

Уравнение прямолинейного равномерного движения в общем виде:

V = V₀ = const и x = x₀ + Vt применительно к данной задаче имеют вид:

V = V_0x

x = V_0x t

Уравнение прямолинейного равноускоренного движения в общем виде:

V = V₀+ at и x = x₀ + V₀ t + at²/2 применительно к данной задаче имеют вид:

V_y = V_0y – gt

y = V_0yt – gt²/2

Теперь имея уравнения движения, можно легко найти любые требуемые величины в данной задаче.

1. Время подъема t­_m до верхней точки h_m можно найти из условия, что вертикальная скорость V_y в этой точке равна нулю: V_y = V_0y – gt_m =0. Отсюда t_m = V_0y /g

Время всего полета t_п, если тело летит до уровня земли можно найти из условия: y(t_п) =0, т.е. y = V_0yt_п – gt_п²/2 =0. Отсюда t_п1 = 0 и t_п2 = 2 V_0y/g. Т.е. t_п = 2 t_m

2. Время всего полета t_п, если тело летит до высоты y=h₁. Условие - y(t_п) =h₁­, т.е.

y = V_0yt_п – gt_п²/2 =h₁.

Решаем это квадратное уравнение t_п = 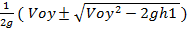. Дискриминант должен быть больше нуля, т.е. V_0y² – 2gh₁ > 0, или 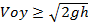₁ В обратном случае решений нет, потому, что тело просто не долетит до высоты h₁. Два корня уравнения соответствуют двум точкам с высотой h₁ на траектории движении тела.

3. Максимальную высоту подъема тела h_m получим, подставив время t_m = V_0y /g подъема в уравнение для координаты h_m = y(t_m) т.е. h_m = V_0yt_m – gt_m²/2 = V_0y²/2g

4. Дальность полета получим умножив время полета t_п на его постоянную скорость вдоль оси Х: L = t_п V_0x. Для случая полета до высоты y = 0 дальность будет: L = 2 V_0y V_0x /g = V₀²/g _* 2 sin α cos α = V₀² /g _* sin 2α. Максимальная дальность будет при sin 2α =1, т.е. при угле броска α =45⁰. L_max = V₀²/g

5. Найдем скорость тела в какой-либо промежуточной точке траектории. Пусть спрашивается скорость через время t₁ после броска. Найдем скорость через ее компоненты вдоль X и Y¸ V_x = V_x0, а V_y = V_y0 – g t₁. Тогда модуль скорости по теореме Пифагора .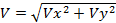

Угол наклона скорости к оси Х найдем через его тангенс: tg α₁ = V_y /V_x = V_x0/ (V_y0 – g t₁)

6. Чтобы построить график траектории движения y(x) запишем уравнение движения вдоль оси X: x = V_0x t и уравнение движения вдоль оси Y: y = V_0yt – gt²/2. Выразим время t из первого уравнения и подставим во второе. Получим: y = V_0y/V_{0x *} x – g/2V_0x² _* x², т.е. траектория движения является параболой.

14. Равномерное движение МТ по окружности. Движение МТ по окружности удобно описывать в полярных координатах (R, ϕ).

Полярная система координат на плоскости представляет собой одну ось координат (полярная ось) и радиус –вектор, начинающейся в точке начала отсчета (полюсе) и заканчивающийся в точке М, положение которой он определяет. Положение этой определяемой точки в полярной системе координат определяется длиной радиус-вектора r (радиальная координата) и углом его поворота относительно полярной оси ϕ (азимут): M(r,ϕ)

Радианная мера угла. Для измерения угла ϕ в физике используется не градусы, а радианы. Радианная мера – это отношение дуги, на которую опирается угол к радиусу: ϕ = _͝͝ AB/R. Полный угол в радианах ϕ_пол= 2π R/R = 2π. Поскольку в градусах полный угол = 360⁰, то 1 рад = 360/2π = 57,3⁰.

Угловая скорость – это скорость изменения радианного угла (азимута) в единицу времени ω = Δϕ/Δt. Размерность угловой скорости: [ω]= 1/сек.

Если материальная точка движется по окружности, то ее путь – это длина дуги окружности ΔL = _͝͝ AB ΔL =Δϕ R. Разделим это равенство на Δt и получим: ΔL/ Δt = R Δϕ\Δt. Но, ΔL/ Δt – это линейная скорость, значит: V = ω R.

Период Т– это время одного оборота при равномерном движении тела по окружности. Когда тело делает полный круг, Δϕ = 2π, а Δt = Т. Угловая скорость ω = Δϕ/Δt = 2π /Т, отсюда: T = 2π/ω.

Частота – это число оборотов в секунду ν = 1/T. Размерность частоты [ν] = 1/c называется Герц (Гц).

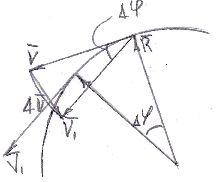При движении по окружности вектор скорости V изменяет свое направление, следовательно – это движение с ускорением. Поскольку модуль вектора не меняется, то это нормальное ускорение, которое перпендикулярно вектору скорости и направлено оно к центру окружности. Оно называется центростремительным. Ускорение по определению а _цс = Δ V /Δt. На рисунке видно, как тело, перемещаясь на угол Δϕ изменяет свою скорость с V на V₁, за счет прибавления ΔV. Из треугольника скоростей видно, что дуга VV₁ = V Δϕ (из определения радианной меры угла). Но дуга VV₁ при малых Δϕ стремится к хорде ΔV. Таким образом, ΔV= V Δϕ. Разделим это уравнение на Δt.

Получим ΔV/ Δt = V Δϕ/Δt = V ω = V²/R. Следовательно, центростремительное ускорение a_цс = V²/R = ω²R.

15. Формулы и константы.

15.1. Равномерное прямолинейное движение Уравнения движения: V=const;

x = x₀ +Vt;

S = Δx = x - x₀ = Vt

15.2. Равноускоренное прямолинейное движение Уравнения движения: а = const;

V(t) = V₀ +at;

x = x₀ + V₀t + at²/2

S = V₀t + at²/2

Координаты вершины параболы: t = - V₀/a; x_m = - V₀²/2a

Соотношение между скоростями: V_к² – V_н² = 2a S

15.3. Движение по вертикали в однородном поле сил тяжести Уравнения движения: V=V₀ – gt;

x = x₀ + V₀t – gt²/2

t_m= V₀/g – время подъема тела на максимальную высоту, x_m=V₀²/2g – максимальная высота.

15.4. Движение тела, брошенного под углом к горизонту Время подъема до верхней точки траектории t_m = V_0y/g, Высота подъема h_max = V_0y²/2g, Время всего полета до точки падения t_к = 2t_m = 2V_0y/g. Дальность полета L = 2V_0yV_0x/g = V₀²/g _* 2sin α cos α = V₀²/g _* sin 2 α Максимальная дальность при α =45⁰ L = V₀²/2g

 

15.5. Равномерное движение по окружности

Угловая скорость ω = Δφ/Δt = 2πν

Связь линейной и угловой скорости V=ωR

Период вращения T = 2π/ω

Частота вращения ν = 1/T = ω / 2π

Центростремительное ускорение а_цс =V²/R = ω²R