Выбор материалов зубчатых колес
Материалы выбираем по табл. 1.1 [1]
Шестерня
Материал
Термическая обработка
Твердость поверхности зуба
Колесо
Материал
Термическая обработка
Твердость поверхности зуба
Определение допускаемых напряжений
Допускаемые контактные напряжения
HPj = 
где j =1 для шестерни, j =2 для колеса;
s H lim j - предел контактной выносливости (табл. 2.1 [1]),
s H lim1 =
s H lim2=
SHj - коэффициент безопасности (табл. 2.1 [1]),
SH 1= SH 2=
KHLj - коэффициент долговечности;
KHLj = 
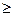1,
здесь NH 0 j – базовое число циклов при действии контактных напряжений (табл. 1.1 [1]),
NH0 1= NH0 2 =
Коэффициент эквивалентности при действии контактных напряжений определим по табл. 3.1 [1] в зависимости от режима нагружения: 
h =
Суммарное время работы передачи в часах
th = 365 L 24 K г К сПВ =
Суммарное число циклов нагружения
N S j = 60 nj c th,
где с – число зацеплений колеса за один оборот, с = 1;
nj – частота вращения j-го колеса, n 1= мин-1, n 2= мин-1;
N S1= N S2=
Эквивалентное число циклов контактных напряжений, NHE j = h N Σj;
NHE 1= NHE 2=
Коэффициенты долговечности
KHL 1= KHL 2=
Допускаемые контактные напряжения для шестерни и колеса
s HP 1=
s HP 2=
Для прямозубых передач s HP =s HP 2, для передач с круговым зубом
s HP = 0.45 (s HP 1 + s HP 2) 
1.15 s HP 2.
Допускаемые контактные напряжения передачи:
s HP =
Допускаемые напряжения изгиба
FPj =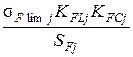 
,
где s F lim j - предел выносливости зубьев при изгибе (табл. 4.1 [1]),
s F lim 1 = s F lim 2 =
SFj - коэффициент безопасности при изгибе (табл. 4.1 [1]),
SF 1=, SF 2=;
KFCj - коэффициент, учитывающий влияние двухстороннего приложения нагрузки, (табл. 4.1 [1]) KFC 1=, KFC 2=
KFLj - коэффициент долговечности при изгибе:
KFL j= 
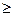1.
здесь qj - показатели степени кривой усталости (табл. 3.1 [1]):
q 1 =, q 2 =;
NF 0 – базовое число циклов при изгибе; NF 0 = 4•106.
NFEj – эквивалентное число циклов напряжений при изгибе; NFE j = Fj N Σ j.
Коэффициент эквивалентности при действии напряжений изгиба определяется по табл. 3.1 [1] в зависимости от режима нагружения и способа термообработки
F 1 =, F2 =,
NFE 1 =, NFE 2 =
KFL 1 =, KFL 2 =
Допускаемые напряжения изгиба: FP 1=
FP2 =
Проектный расчет передачи
Внешний делительный диаметр колеса определяем из условия контактной прочности:
de 2 = 1650 
,
где 
- коэффициент снижения несущей способности зуба конического колеса по сравнению с зубом цилиндрического колеса при действии контактных напряжений;
KН - коэффициент контактной нагрузки, на этапе проектного расчета примем KН = 1.2.
Для прямозубых передач принимают = 0.85, для передач с круговым зубом вычисляют по формулам табл. 14.1 [1].
Расчетное значение de 2
de 2 =
Округлим de 2 до стандартного значения (табл. 12.1 [1]): de 2 =
Внешний модуль предварительно определим по формуле
me = 
=
где 
- коэффициент снижения несущей способности зуба конического колеса по сравнению с зубом цилиндрического колеса при действии напряжений изгиба (табл.14.1 [1]), =
Округлим me до стандартного значения (табл.11.1 [1]): me =
Число зубьев колеса Z 2 = 
=
Число зубьев шестерни Z 1 =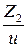 
=
Фактическое передаточное число u ф = 
=
Отклонение фактического передаточного числа от номинального
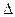u = 100 
=
Внешний делительный диаметр шестерни
de 1= me Z 1 =
de 2= me Z 2 =
Углы делительных конусов колеса и шестерни:
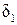= arctg 
=
= 
– 
=
Внешнее конусное расстояние Re = 
=
Ширина зубчатого венца b = 0.285 Re.
Ширину венца округлим до ближайшего числа из ряда нормальных линейных размеров (c.12 [1]): b =
Уточним значение коэффициента ширины зубчатого венца 
= 
.=
Коэффициенты смещения шестерни и колеса
x 1 = 2 
=
x 2 = – x 1 =
где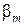 
=35° - угол наклона средней линии зуба.
Средняя окружная скорость в зацеплении
V = 
=
где dm 1 = de 1(1 – 0.5 ) - средний делительный диаметр шестерни,
С учетом окружной скорости назначим степень точности передачи n cт =