1. Постановка задачи. Математическая модель
Рассматриваем задачу об одновременном изгибе и сжатии стержня. Даже в малых перемещениях, она нелинейна (см. лекцию 3) и не имеет аналитического решения. Численное же решение не представляет проблем. Однако с целью пояснения сути проблемы и общих свойств задачи рассмотрим сначала частный случай, позволяющий получить аналитическое решение и его анализировать: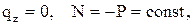 
Р известно, w не вычисляем. Тогда из (5.5) имеем
, 
, 
, 
.
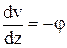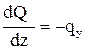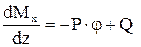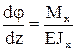Задача сводится к линейному дифференциальному уравнению 4-го порядка
(*)
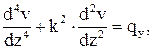где
. (**)
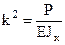Решение – сумма общего решения однородного уравнения и частного решения уравнения с правой частью:
.
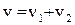Решение однородного уравнения методом Эйлера известно. В итоге
. (***)
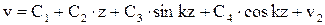Где С1 … С4 – произвольные постоянны, определяемые из граничных условий (условий закрепления), которые для типичных случаев приведены в таблице.
Таблица
| Номер схемы | Схема опирания и нагружения | Граничные условия | Ркр | |
| 
| |||
|  ,
| ,
| 
| |
| ,
 
| ,
| 
| |
| ,
|
| 
| |
| ,
| ,
| 
| |
| ,
|
|
| |
| ,
|
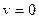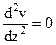
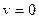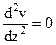
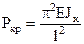
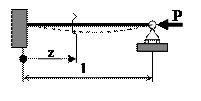
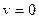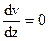
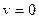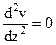
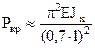
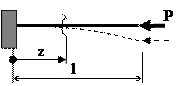
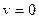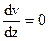
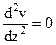
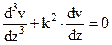
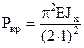
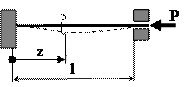
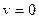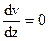
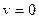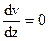
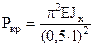
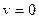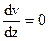
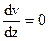
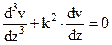
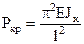
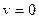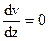
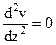
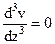
| Нет решения, определитель тождественно равен 1 |
2. Решение задачи о значении критической сжимающей силы.
С учетом граничных условий формируется система линейных алгебраических уравнений для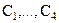 
. Положим, решаем систему методом Крамера. Если определитель системы при некотором Р=Ркр (т.е.k) обращается в нуль, то прогибы стремятся к бесконечности. Найдя минимальный корень 
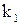соответствующего трансцендентного уравнения, определяем критическую силу
.
В схеме 2 не удается найти аналитическое решение трансцендентного уравнения и оно решено численно (приближенно).
В схеме 6 решение отсутствует. В этом случае необходимо применить динамический метод для окончательного решения вопроса о критической силе.
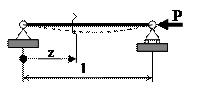
Проиллюстрируем изложенный алгоритм на примере схемы 1.
Система линейных алгебраических уравнений для 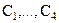имеет вид
.
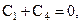
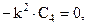
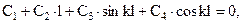
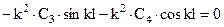Равенство нулю определителя системы
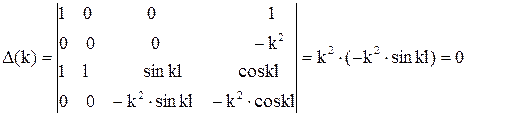
приводит к трансцендентному уравнению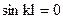 
, решение которого
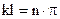. т.е. 
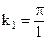и .
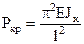Аналогично получены критические силы для остальных схем.
Интересен вопрос о зависимости решения от соотношения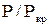 
.
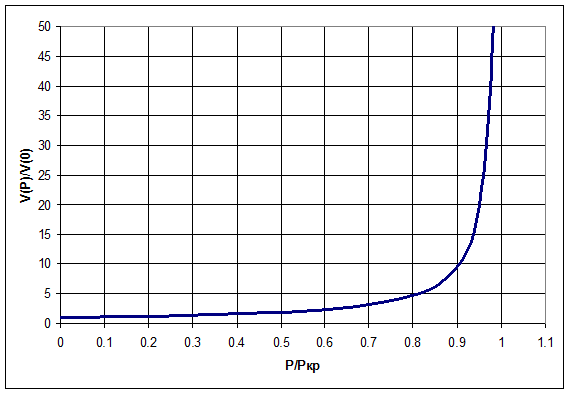Результат численного решения представлен на графике. При Р/Ркр 
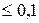решение мало отличается от простого изгиба. При Р/Ркр 
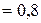решение в ≈5 раз больше и т.д.
3. Расчет на прочность
Расчет на прочность при продольно-поперечном изгибе ведут следующим образом.
· Кроме обычного расчета проверяют запас по критической силе.
· Поскольку критическая сила определяется при малых перемещениях и в упругой области, то проверяется условие
,
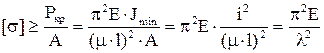откуда предельное значение гибкост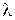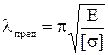и 
и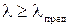 
.
· Если условие выполняется, то критическая сила вычисляется по формуле
, (****)
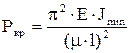где коэффициент приведения длины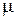 
зависит от способа закрепления стержня и места приложения силы и приводится в таблицах.
· Если условие не выполняется, то по таблицам (построенным Ясинским), в зависимости от 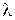определяется коэффициент 
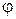снижения допускаемых напряжений и проверяется условие
.
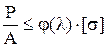При численном решении задачи возможен учет пластических деформаций и больших перемещений и расчет можно вести по допускаемым напряжениям.
4. Приближенное определение критической сжимающей силы
В тех случаях, когда аналитическое решение невозможно или очень громоздко (погонная сжимающая нагрузка, сила не на конце стержня, комбинация нагрузок) традиционно применяется приближенное решение на основе теоремы Лагранжа-Дирихле. Вид функции прогибов выбирается приближенно, но удовлетворяющий граничным условиям. Составляется выражение для суммы потенциальной энергии деформации стержня и работы сжимающих сил и приравнивается нулю. Из этого уравнения вычисляется критическая сила или их комбинация и, по формуле (****), коэффициент 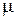. Результат вычисления критической нагрузки всегда больше фактического, так как согнуть стержень «неестественно» труднее, чем естественно. Т.е. запас нужно увеличивать в сравнении с точным решением. Метод нами рассматриваться не будет ввиду его громоздкости. Тема вынесена на самостоятельное изучение.
Гораздо более эффективно численное решение на ЭВМ и метод неидеальностей. Интегрируем численно систему (5.5) или (5.4) (пунктирная кривая) при небольшой изгибающей нагрузке последовательно увеличивая сжимающую нагрузку, и строим график как на рисунке выше. При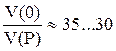 
надежно получаем критическую нагрузку с некоторым запасом (
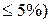. Именно этим способом мы будем определять критическую нагрузку и значение 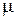при выполнении расчетно-графических работ.