Примеры выполнения практических заданий
Пример 1. При проведении измерительного эксперимента получены следующие значения величины: 11,65; 11,41; 11,57; 11,60; 11,50; 11,55; 11,58; 11,58; 11,61; 11,63. Требуется проанализировать полученные результаты наблюдений в целях выявления грубых погрешностей, используя критерий Диксона.
Решение:
1. Располагаем результаты наблюдений в вариационный возрастающий ряд:
11,41<11,50<11,55<11,57<11,58;11,58<11,60<11,61<11,63<11,65.
2. Записываем используемую для расчета формулу критерия Диксона:
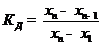 .
.
3. Подставляем в формулу данные нашего эксперимента и рассчитываем Кд:
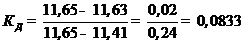 .
.
4. Зададимся значением q=0,10 (десятипроцентным уровнем значимости).
5. Используя табличные данные, выявим критическую область для рассчитанного критерия Кд.
Согласно таблице 2 приложения 3 при n=10 и q=0,15, zдикс =0,35.
6. Делаем вывод, что Кд < zдикс.
Ответ. Полученный ряд результатов наблюдений не имеет в своем составе грубых погрешностей даже при q=0,1. Дальнейшей обработке будет подвергаться весь массив данных.
Пример 2. В процессе контроля были получены следующие результаты измерительных наблюдений за одним из показателей качества: 9,47; 9,49; 9,40; 9,61; 9,39; 9,41; 9,43; 9,49; 9,46; 9,42. Используя критерий Романовского выявить наличие промахов.
Решение:
1. Располагаем результаты в вариационный возрастающий ряд: 9,39<9,40<9,41<9,42<9,43<9,46<9,47<9,49<9,49<9,61.
2. Выявляем результат, вызывающий сомнение:
Результат 9,61 вызывает сомнение, так как резко отличается от всех остальных (хi=9,61).
3. Запишем основную расчетную формулу:
 .
.
При расчете  результат хi=9,61 все принимаем во внимание.
результат хi=9,61 все принимаем во внимание.
4. Вычисляем среднее арифметическое без учета сомнительного варианта
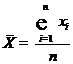 ;
;
n=10-1=9
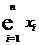 =9,39+9,40+9,41+9,42+9,43+9,46+9,47+9,49+9,49=84,96
=9,39+9,40+9,41+9,42+9,43+9,46+9,47+9,49+9,49=84,96
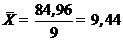
5. Находим среднеквадратическое отклонение среднего арифметического результата наблюдения по формуле
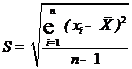 ;
;
Разность хi – 
| Квадрат разности | 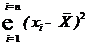
|
х1-  =9,39-9,44=-0,05 =9,39-9,44=-0,05
| 0,0025 | 0,0118 |
х2-  =9,40-9,44=-0,04 =9,40-9,44=-0,04
| 0,0016 | |
х3-  =9,41-9,44=-0,03 =9,41-9,44=-0,03
| 0,0009 | |
х4-  =9,42-9,44=-0,02 =9,42-9,44=-0,02
| 0,0004 | |
х5-  =9,43-9,44=-0,01 =9,43-9,44=-0,01
| 0,0001 | |
х6-  =9,46-9,44=0,02 =9,46-9,44=0,02
| 0,0004 | |
х7-  =9,47-9,44=0,03 =9,47-9,44=0,03
| 0,0009 | |
х8-  =9,49-9,44=0,05 =9,49-9,44=0,05
| 0,0025 | |
х9-  =9,49-9,44=0,05 =9,49-9,44=0,05
| 0,0025 |
Определяем число степеней свободы f=n-1=9-1=8
Рассчитываем стандартное отклонение:
 ;
;
6. Подставляем полученные расчетные данные в основную формулу (14):
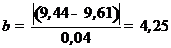 .
.
7. Находим табличное значение критерия Романовского 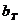 для n =10 и принятого уровня значимости q=0,1:
для n =10 и принятого уровня значимости q=0,1: 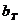 =2,29.
=2,29.
8. Вывод: рассчитанное значение 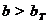 .
.
Ответ: Так как 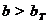 сомнительный результат наблюдения равный 9,61 является грубой погрешностью и в дальнейшей обработке полученных данных не используется.
сомнительный результат наблюдения равный 9,61 является грубой погрешностью и в дальнейшей обработке полученных данных не используется.
Пример 3. Некоторую физическую величину измерили двумя независимыми способами. По первому способу получили результаты:38.20,38.00,37.66; по второму – 37.70,37.65,37.55. Значимо ли различаются результаты данных измерений?
Решение:
1. По формуле (6) рассчитаем среднее арифметическое значение для каждого способа:
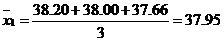 и
и 
2. Рассчитаем дисперсии 
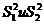 по формуле (8):
по формуле (8):
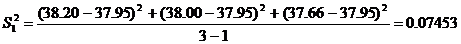
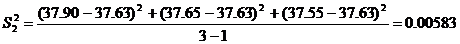
3. Проведем сравнение точности обоих методов, используя F-распределение:
Fэксп = 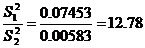
Полученные значения Fэксп, сопоставляем с табличным (таблица 6, приложения 3) значением F распределения при р=0.95 и числах степеней свободы f 1 =2 и f 2 =2.
Так как F табл= 19.00> F эксп=12.78, то расхождение между дисперсиями незначимо и, следовательно, способ измерения физической величины одинаковой точности.
С помощью t-критерия оцениваем расхождение между 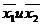 . Среднее взвешенное двух дисперсий и t-критерий рассчитываем по формулам
. Среднее взвешенное двух дисперсий и t-критерий рассчитываем по формулам
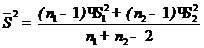 и
и 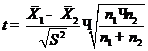 , тогда
, тогда
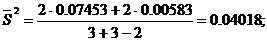
t эксп = 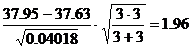
Сопоставляем полученное значение t эксп с табличными t 0.95;4 = 2,776 (при р= 0,95 и f = 3+3-2=4). Так как t эксп =1.96 < t 0.95;4 = 2,776, то различие между 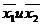 незначимо. Следовательно, все результаты обоих измерений отражают истинное значение физической величины.
незначимо. Следовательно, все результаты обоих измерений отражают истинное значение физической величины.
Поэтому данные измерения могут быть представлены в виде
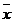
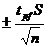 ;
;
где 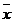 – среднее арифметическое из всех n1+n2 результатов:
– среднее арифметическое из всех n1+n2 результатов:
4. Вычисляем среднее значение измерений (среднее арифметическое) по формуле (1):
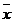 =
= 
Определим среднее квадратическое отклонение S по формуле (9):
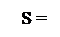

Рассчитаем доверительные границы действительного значения результата измерения, исходя из данных наблюдений, полученных обоими способами, по формуле (15). Для расчета необходимое значение t0,95;5 находим по таблице (см. приложение 3, табл. 1)
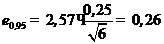
Ответ. Результат измерений физической величины, рассчитанный по данным наблюдений полученных двумя способами, записываем следующим образом: 37.79 ±0.26.
Пример 4. При измерении некоторой величины были получены следующие результаты: 1.31, 1.45,1.42,1.32, 1.30. Опорное значение этой величины Хоп = 1,47.
Определить стандартное отклонение S, точность измерений 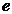 0.95 (
0.95 ( ,%) и сделать вывод о наличии систематической ошибки в использовании данного метода измерения.
,%) и сделать вывод о наличии систематической ошибки в использовании данного метода измерения.
Решение:
1. По формуле (6) вычисляем среднее значение измерений (среднее арифметическое):
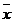 =
= 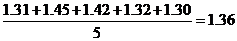
2.По формуле (9) вычисляем стандартное отклонение S:
S = 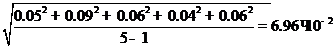 ;
;
3.По формуле (15) рассчитываем доверительные границы случайной составляющей погрешности результата измерения. Значение коэффициента Стьюдента находим из таблицы (см. приложение 3, табл.1).
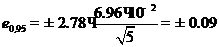
4. Покажем доверительный интервал действительного значения величины:
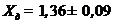 ;
;
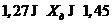
5. Точность метода обычно выражают в форме относительной погрешности, которая рассчитывается по формуле (22)
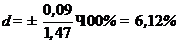
Ответ. Данный метод измерения НКПРП имеет систематическую погрешность, так как опорное значение Хоп = 1,47 не попадает в доверительный интервал 1,27  1,45. Точность измерения
1,45. Точность измерения 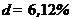 является очень низкой для данного метода.
является очень низкой для данного метода.
Пример 5. Определить, существует ли значимое различие между выборочной средней величиной при определении НКПРП пыли обращающейся в производстве, если при отборе проб следующие результаты: 2.10, 2.12, 2.13, 2.15, 2.15 и средней генеральной совокупностью (для n =80) m =2.15 г/м3.
Решение:
1.Среднее арифметическое значение вычисляем по формуле (6):
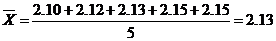
2.Стандартное отклонение отдельного определения вычисляем по формуле (9):
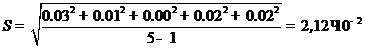 ,
,
3.Из формулы (15) находим значение величины t:
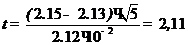
Из таблицы значений коэффициента Стьюдента (смотри таблицу 1 приложения 3) для f =4 и p =0,95, tр,f =2,78, что больше рассчитанного из формулы (15)  2,11.
2,11.
Ответ. Следовательно, средняя величина 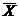 не отличается значимо от средней m генеральной совокупности.
не отличается значимо от средней m генеральной совокупности.
Пример 6. При определении коэффициента теплопроводности 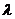 газобетона были получены результаты: 8.0×10–4 Вт/моС и 8.4×10–4 Вт/моС. Чему равна точность изменения (eр и D) коэффициента теплопроводности? Сколько параллельных измерений необходимо провести для достижения относительной точности 5%? Оправдано ли будет применение этого способа измерения для достижения такой точности?
газобетона были получены результаты: 8.0×10–4 Вт/моС и 8.4×10–4 Вт/моС. Чему равна точность изменения (eр и D) коэффициента теплопроводности? Сколько параллельных измерений необходимо провести для достижения относительной точности 5%? Оправдано ли будет применение этого способа измерения для достижения такой точности?
Решение:
1. По формуле (6) находим среднее арифметическое значение:
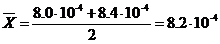
2.Стандартное отклонение единичного результата вычисляем по формуле (9):
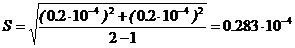 ,
,
По таблице 1 приложения 3 находим для р =0.95 и f =2-1=1 tр,f =12.7 и по формуле (15) вычисляем точность метода:

3. Определяем относительную точность измерения по формуле (22):
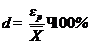
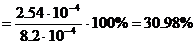
Если необходимо получить D=5%, то
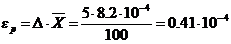 или
или 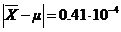
Из формулы (15)

Если принять n =4, то t =2.90. Исходя из данных таблице 1 (см. приложение 3) для р =0.95 и f =4–1=3 tр,f =3.18, что не обеспечивает точности 5%. Если принять n =5, то t =3.24. По таблице 1 (см. приложение 3) для р =0.95 и f =5–1=4 tр,f =2.78, что меньше рассчитанного t =3.24. Следовательно, при n =5 величина t =3.24 дает большую вероятность, чем 0.95.
Ответ. Для достижения относительной погрешности 5% необходимо провести 5 измерений. Так как n <8 (n =5), то можно считать, что данный метод вполне оправдан для достижения точности 5%.
Пример 7
Пример построения гистограммы и проверка гипотезы о распределении случайной величины
Даны 98 независимых равноточных измерений некоторой физической величины:
120.13 120.76 119.39 118.88 121.11 121.66 119.58
118.49 119.00 119.18 120.90 120.53 121.92 119.76
121.19 121.35 120.16 119.31 121.25 119.96 120.84
117.17 120.82 119.59 120.57 119.67 119.92 120.51
121.76 121.31 119.61 119.62 120.59 119.00 119.85
119.95 119.43 121.07 121.84 122.21 120.20 119.56
119.37 119.34 120.89 120.06 119.95 121.47 119.65
119.90 119.75 120.50 119.99 119.54 120.87 120.25
119.55 119.01 120.03 120.71 120.10 118.73 120.90
120.31 119.83 121.46 122.21 118.40 119.36 120.86
119.72 119.22 119.91 120.62 120.63 119.56 120.07
121.68 120.80 120.16 119.92 121.03 120.17 119.43
119.85 120.52 120.45 119.57 121.11 120.06 120.02
121.64 119.91 119.42 119.31 121.39 120.06 119.55
Рассчитать:
1. При уровне значимости 0.05 исследовать предложенную выборку на однородность. Исключить все грубые ошибки с вероятностью 1– q. Найти среднее значение и эмпирический стандарт S полученной однородной выборки.
2. Сгруппировать однородную выборку по интервалам, построить гистограмму относительных частот, сформировать гипотезу о виде распределения случайной величины Х.
3. Проверить гистограмму о распределении величины Х по критерию согласия Пирсона, установить вероятность р, с которой высказанная гипотеза не согласуется с истинным распределением. Если р <0.50, то данную гипотезу не отвергать, остановиться на данном виде распределения и перейти к пункту 4. Если р >0.50, то выбрать другой закон распределения и снова применить к нему критерий согласия Пирсона. Если при исследовании гипотез о трех различных распределениях (нормальном, логарифмическом и распределении Вейбулла) вероятность несогласования р >0.50, то выбрать лучшее по вероятности распределения.
4. Найти доверительный интервал для математического ожидания M (X)= m и среднего квадратичного отклонения s(X)=s, если задан уровень значимости q, полученной в пункте 3 при выборе распределения величины Х.
Решение:
1. Исследуем данную выборку на однородность. Для этого все результаты измерений расположим в порядке возрастания. Результат запишем в виде табл. 1.
По условию требуется проверить, не содержит ли данная выборка грубых ошибок на уровне значимости 0.05, то есть из выборки следует исключить те хi, которые с вероятностью 1– q =0.95.
Найдем критическое значение числа
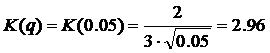 ,
,
с которым будем сравнивать максимальное отклонение t (xi). Нанесем на ось все значения из табл. 6.1.
Табл. 6.1. Экспериментальные значения величины Х
| I | xi | i | xi | i | xi | i | xi |
| 117.17 118.40 118.49 118.73 118.88 119.00 119.00 119.01 119.18 119.22 119.31 119.34 119.35 119.36 119.37 119.37 119.39 119.42 119.43 119.43 119.54 119.55 119.55 119.56 119.56 | 119.57 119.58 119.59 119.61 119.62 119.65 119.72 119.75 119.76 119.83 119.85 119.85 119.90 119.91 119.91 119.92 119.92 119.95 119.95 119.96 119.99 120.02 120.03 120.06 120.06 | 120.06 120.07 120.10 120.13 120.16 120.16 120.17 120.20 120.25 120.31 120.45 120.50 120.51 120.52 120.53 120.57 120.59 120.62 120.63 120.71 120.76 120.80 120.82 120.84 120.86 | 120.87 120.89 120.90 120.90 121.03 121.07 121.11 121.11 121.19 121.25 121.31 121.35 121.39 121.46 121.47 121.64 121.66 121.68 121.76 121.84 121.92 122.21 122.21 |
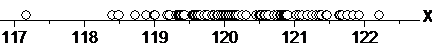
Рис. 6.1. Распределение случайной величины
Как можно видеть из рис. 6.1, наиболее густо точки расположены в интервале [119, 122]. Значение x 1=117.17 резко отличается от интервала [119, 122], что может служить косвенным подтверждением того, что величина x 1 является грубой ошибкой. Остальные значения xi не вызывают особых подозрений, поэтому мы исследуем дополнительно крайние точки x 1, x 2, x 97 и x 98.
Временно отбросив указанные значения, подсчитаем среднее арифметическое значение и эмпирический стандарт:
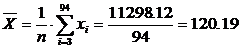 ;
;
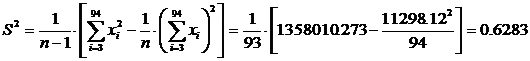 и
и 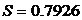 .
.
Исследуем сначала x 1=117.17, применив к нему наш критерий. Оказалось, что  . Исходя из приведенного расчета видно, что значение
. Исходя из приведенного расчета видно, что значение 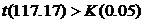 . Следовательно, x 1=117.17 является грубой ошибкой, и поэтому данное значение должно быть исключено из результатов обработки.
. Следовательно, x 1=117.17 является грубой ошибкой, и поэтому данное значение должно быть исключено из результатов обработки.
Применим t -критерий к значению x 2=118.40. Расчет значения t -критерия дает следующую величину  . Так как
. Так как 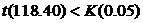 , то включив в выборку x 2=118.40, пересчитаем с учетом его
, то включив в выборку x 2=118.40, пересчитаем с учетом его 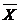 и
и 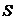 .
.
Получим
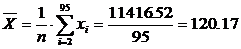 ;
;
 и
и 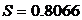 .
.
Вычислим 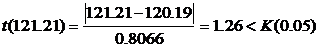 . Таким образом, значения x 97= x 98=121.21 также принадлежат к выборке, поэтому включаем их в выборку и с вероятностью 1– р =0.95 выборка, представленная в табл. 6.1, является однородной.
. Таким образом, значения x 97= x 98=121.21 также принадлежат к выборке, поэтому включаем их в выборку и с вероятностью 1– р =0.95 выборка, представленная в табл. 6.1, является однородной.
Для полученной выборки находим
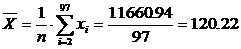 ;
;
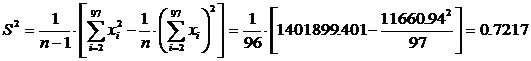 и
и 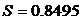 .
.
2. Сгруппируем данные табл. 6.1 по интервалам с шагом, вычисленным по соотношению
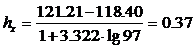 .
.
Начальная точка равна 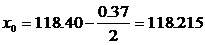 .
.
Найдем границы интервалов 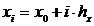 , включающих все данные табл. 6.1, а также подсчитаем, сколько значений величины Х попадает в каждый интервал, то есть найдем частоты ni. Результаты запишем в табл. 6.2.
, включающих все данные табл. 6.1, а также подсчитаем, сколько значений величины Х попадает в каждый интервал, то есть найдем частоты ni. Результаты запишем в табл. 6.2.
По данным табл. 6.2 построим гистограмму. Для этого отложим на оси х интервалы длиной 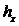 и начертим гистограмму.
и начертим гистограмму.
Табл. 6.2. Расчет высоты прямоугольников для построения гистограммы
| I | Интервал xi | Число попаданий в i -ый интервал | 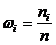
| 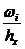
|
| 118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285 | 0.0206 0.0206 0.0619 0.2062 0.2062 0.0928 0.1237 0.1134 0.0722 0.0515 0.0309 | 0.0557 0.0557 0.1673 0.5573 0.5573 0.2508 0.3343 0.3065 0.1951 0.1392 0.0835 |
3. Предположим, что случайная величина распределена по нормальному закону распределения с параметрами 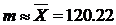 и
и  . Гипотезу о нормальном распределении случайной величины Х проверим по критерию согласия Пирсона.
. Гипотезу о нормальном распределении случайной величины Х проверим по критерию согласия Пирсона.
Результаты вычислений занесем в табл. 6.3.
Для заполнения табл. 6.3 в столбец 2 занесем из табл. 6.2 концы интервалов xi; затем заполняем столбец 3 по формуле 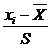 . Далее находим значение функции Лапласа по данным табл. 7 приложения 3, используя линейное интерполирование. Считаем при x 0= –¥ и x 10= +¥. Теоретическую вероятность находим по формуле (70) и записываем результаты между строк столбца 4. Затем вычисляем
. Далее находим значение функции Лапласа по данным табл. 7 приложения 3, используя линейное интерполирование. Считаем при x 0= –¥ и x 10= +¥. Теоретическую вероятность находим по формуле (70) и записываем результаты между строк столбца 4. Затем вычисляем 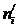 и
и  выпишем
выпишем 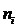 из табл. 6.2.
из табл. 6.2.
Для расчета критерия Пирсона объединим первые и последние два интервала. Используя данные табл. 6.3, рассчитаем критерий согласия Пирсона 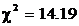 . Число интервалов К =9. Число параметров, для которых были найдены оценки, r =2. Число степеней свободы f = К – r –1=9–2–1=6. В табл. 4 приложения 3 находим, что 12.6<
. Число интервалов К =9. Число параметров, для которых были найдены оценки, r =2. Число степеней свободы f = К – r –1=9–2–1=6. В табл. 4 приложения 3 находим, что 12.6< 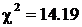 <14.4. Следовательно, число 12.6 соответствует р =0.95, а число 14.4 соответствует р =0.975, то есть гипотеза о нормальном распределении не согласуется с истинным распределением с вероятностью 0.95–0.975 и мы имеем веские основания для принятия гипотезы о нормальном распределении случайной величины.
<14.4. Следовательно, число 12.6 соответствует р =0.95, а число 14.4 соответствует р =0.975, то есть гипотеза о нормальном распределении не согласуется с истинным распределением с вероятностью 0.95–0.975 и мы имеем веские основания для принятия гипотезы о нормальном распределении случайной величины.
Табл. 6.3. Проверка гипотезы о нормальном распределении величины Х
| i | xi | 
| 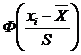
| pi | 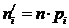
| 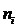
|
| 118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285 | – –1.9247 –1.4891 –1.0536 –0.6180 –0.1825 0.2531 0.6886 1.1242 1.5597 1.9953 + | –0.5000 –0.4729 –0.4320 –0.3545 –0.2317 –0.0724 0.0999 0.2318 0.3857 0.4404 0.4764 0.5000 | 0.0271 0.0409 0.0775 0.1228 0.1593 0.1723 0.1319 0.1539 0.0547 0.0360 0.0236 | 2.6287 3.9673 7.5175 11.9116 15.4521 16.7131 12.7943 14.9283 5.3059 3.4920 2.2892 | ||
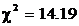
|
На гистограмме относительных частот (рис. 6.2) максимум сдвинут влево от середины интервала [118.4, 122.2], поэтому здесь вероятнее всего предложить наличие логарифмически нормального распределения или закона Вейбулла, чем нормального закона распределения.
Предположим сначала, что данное распределение подчинено закону Вейбулла и оценим сначала параметры a и b по формулам (67) и (68).
Найдем значение статистической функции F 97(x) для концов интервалов из табл. 6.2. Так, например, значение 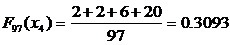 . Результаты остальных расчетов приведены в табл. 6.4.
. Результаты остальных расчетов приведены в табл. 6.4.
Табл. 6.4. Проверка гипотезы о распределении величины Х по закону Вейбулла [1]
| i | xi | F 97(x) | 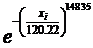
| pi | 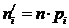
| 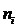
|
| 118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285 | 0.0206 0.0412 0.1031 0.3093 0.5155 0.6082 0.7320 0.8454 0.9175 0.9691 1.0000 | 0.9208 0.8771 0.8120 0.7189 0.5931 0.4379 0.2716 0.1281 0.0394 0.0062 0.0003 3.69·10–6 | 0.0437 0.0651 0.0931 0.1258 0.1552 0.1663 0.1435 0.0887 0.0332 0.0059 0.0003 | 4.2389 6.3147 9.0307 12.2026 15.0932 16.1311 13.9195 8.6039 3.2204 0.5723 0.0291 | ||
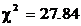
|
С помощью табл. 6.4 решим уравнение F 97(t 1)=0.75 и F 97(t 2)=0.25. Число 0.75 находится между F 97(120.435)=0.7320 и F 97(120.805)=0.8454.
Составим уравнение прямой, проходящей через точки с этими координатами: 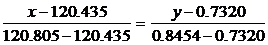 . Предположим, что точка с координатами (t 1; 0.75) лежит на этой прямой, то есть х = t 1, у =0.75. Тогда
. Предположим, что точка с координатами (t 1; 0.75) лежит на этой прямой, то есть х = t 1, у =0.75. Тогда 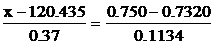 . Отсюда будем иметь
. Отсюда будем иметь 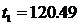 .
.
Аналогично найдем t 2 из условия, что F 97(t 2)=0.25:
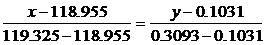 ;
; 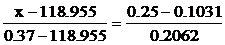 ;
; 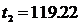 .
.
Затем найдем оценки параметров 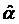 и
и 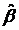 :
:
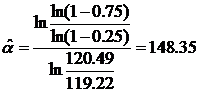 ;
; 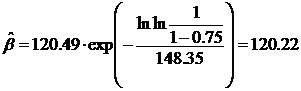 .
.
Таким образом, предполагаемая функция плотности вероятности имеет вид
 ,
,
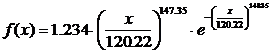 .
.
Проверим, насколько это распределение Вейбулла согласуется с истинным распределением, используя критерий согласия Пирсона. Для расчета критерия Пирсона объединим первый и второй интервалы и восьмой–одиннадцатый интервалы. Результаты вычислений заносим в табл. 6.4: 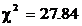 . В табл. 4 приложения 3 находим, что
. В табл. 4 приложения 3 находим, что 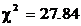 >14.9 (при f = К – r –1=7–2–1=4). Следовательно, число 14.9 соответствует р =0.995, то есть гипотеза о распределении Вейбулла не согласуется с истинным распределением с вероятностью p >0.995 и мы имеем веские основания для отвержения гипотезы о распределении случайной величины по закону Вейбулла.
>14.9 (при f = К – r –1=7–2–1=4). Следовательно, число 14.9 соответствует р =0.995, то есть гипотеза о распределении Вейбулла не согласуется с истинным распределением с вероятностью p >0.995 и мы имеем веские основания для отвержения гипотезы о распределении случайной величины по закону Вейбулла.
Выдвинем гипотезу о логарифмически нормальном распределении. Оценим параметры этого распределения по формулам (58) и (59). Находим, что
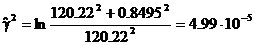 ;
; 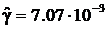 ;
; 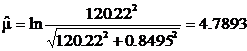 .
.
Тогда предполагаемая функция вероятностей имеет вид
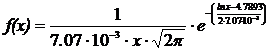 ;
; 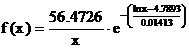 .
.
Сделаем проверку гипотезы о логарифмически нормальном распределении по критерию согласия Пирсона (табл. 4 приложения 3).
Как можно видеть, значение критерия 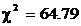 велико, следовательно, логарифмически нормальное распределение отклоняется.
велико, следовательно, логарифмически нормальное распределение отклоняется.
Табл. 6.5. Проверка гипотезы о логарифмически нормальном распределении величины Х
| i | xi | 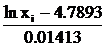
| 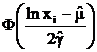
| pi | 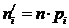
| 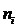
|
| 118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285 | – –0.9674 –0.7467 –0.5272 –0.3081 –0.0896 0.1281 0.3452 0.5616 0.7774 0.9925 + | –0.5000 –0.3336 –0.2721 –0.2009 –0.1209 –0.0357 0.0510 0.1350 0.2128 0.2815 0.3395 0.5000 | 0.1664 0.0615 0.0712 0.0800 0.0852 0.0867 0.0840 0.0778 0.0687 0.0580 0.1605 | 16.1408 5.9655 6.9064 7.7600 8.2644 8.4099 8.1480 7.5466 6.6639 5.6260 15.5685 | ||
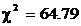
|
Исходя из приведенного расчета видно, что наиболее удачно приведенное распределение описывает нормальное распределение величины Х. Таким образом, окончательное уравнение имеет вид
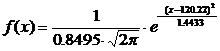 .
.
4. Поскольку распределение величины Х не является нормальным, но число опытов достаточно велико (n =97>30), мы воспользуемся приближенными формулами (73) и (74).
При подборе распределения величины Х значение р Î[0.95, 0.975]. Исходя из этого, принимаем, что величина q= 0.05. По табл. 7 приложения 3 значение аргумента 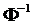 соответствует значению функции
соответствует значению функции 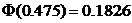 , тогда
, тогда 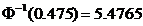 . Тогда
. Тогда
 и
и 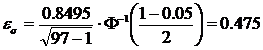
и с вероятностью »0.95 имеем 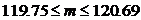 , а также
, а также 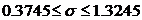 .
.
Пример 8
С помощью тестера (мультиметра), работающего в режиме измерения переменного напряжения, получено значение Uизм=120 В. Диапазон измерений прибора от 0 до 50 В. В паспорте указано, что при работе в этом диапазоне относительная погрешность  не превышает двух процентов. Записать результат измерения.
не превышает двух процентов. Записать результат измерения.
Решение:
1. Результат измерения обычно записывается в форме: Хд=Хизм+  Х; для нашего случая эта запись будет иметь вид
Х; для нашего случая эта запись будет иметь вид
Uд= Uизм+  U, при относительной погрешности
U, при относительной погрешности  ,
,
где Uизм – измеренное значение (120 В);  U – абсолютная погрешность измерения;
U – абсолютная погрешность измерения;  - относительная погрешность (2%).
- относительная погрешность (2%).
2. Абсолютная погрешность определяется из формулы:
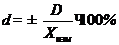 , откуда
, откуда 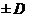 U=
U= 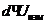 /100%
/100%
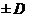 U=2%*120 В/100%=2,4 В.
U=2%*120 В/100%=2,4 В.
Ответ: Результат измерения записывается в виде U = (120,0 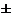 2,4 В) при
2,4 В) при  =
= 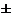 2 %. Запись 120,0 применяется, исходя из записи погрешности, имеющей знак после запятой (2,4). Поэтому при записи результата измерения это учитывается.
2 %. Запись 120,0 применяется, исходя из записи погрешности, имеющей знак после запятой (2,4). Поэтому при записи результата измерения это учитывается.
Пример 9
Для выполнения измерений применялось средство измерения с классом точности 2,5, со шкалой, проградуированной от 0 до 5 и ценой деления 0,2. Было получено значение величины A=3. Записать результат измерения.
Решение:
1. Результат измерения записывается обычно в форме
Ад=Аизм 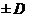 А при относительной погрешности
А при относительной погрешности  ,%,
,%,
где Аизм – измеренное значение величины,  А – абсолютная погрешность,
А – абсолютная погрешность,  относительная погрешность.
относительная погрешность.
Для решения задачи вспомним обозначение погрешностей через класс точности измерительного прибора.
2. Если класс точности обозначим 2,5, это означает, что приведенная погрешность  н = 2,5%.
н = 2,5%.
Воспользуемся формулой приведенной погрешности:
 ,
,
где Ан – ширина диапазона измерений.
Из этой формулы следует, что
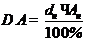 , тогда
, тогда
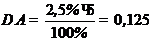 .
.
Относительная погрешность измерения рассчитывается по формуле:
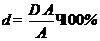 .
.
 .
.
Ответ: Результат измерения запишем Ад=(3,000 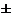 0,125) при относительной погрешности
0,125) при относительной погрешности  .
.
Число знаков после запятой в записи результата и погрешности должно быть одинаково.
Пример 10
Для выполнения измерений применялось средство измерения с классом точности  , со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=4. Записать результат измерения.
, со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=4. Записать результат измерения.
Решение:
Решение задачи осуществляется аналогично примеру 9.
1. Если класс точности обозначается  , это значит, что относительная погрешность
, это значит, что относительная погрешность  =5,0%. Тогда
=5,0%. Тогда
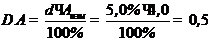
Ответ: Результат измерения запишется как А=4,0 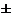 0,5 при
0,5 при  =5,0%.
=5,0%.
Пример 11
Для выполнения измерений применялось средство измерения с классом точности 2,5/1,0, со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=6. Записать результат измерения.
Решение:
1. Если класс точности обозначается 2,5/1,0, это значит, что указаны приведенные погрешности в конце и в начале диапазона измерений соответственно: 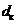 =2,5%,
=2,5%, 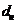 =1,0%.
=1,0%.
Для расчета относительной погрешности результата измерения  используется формула
используется формула
 ,%, т.е.
,%, т.е.
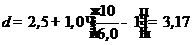 %.
%.
2. Рассчитываем абсолютную погрешность измерения
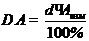 ,
,
 (единицы измерения)
(единицы измерения)
Ответ: Результат измерения запишется как А=6,00 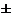 0,19 при
0,19 при  =3,17%.
=3,17%.
Примечание.
Если будем иметь данное не об одном, а о нескольких результатах наблюдения одной и той же величины, полученных с использованием одного и того же средства измерения, то следует с начала определить среднее арифметическое значение, которое и будет приниматься за измеренное значение.
Пример 12
Необходимо определить степень согласованности мнения пяти экспертов. Результаты мнения экспертов представлены следующим образом.
| №1 | - | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 |
| №2 | - | Q3 | Q1 | Q2 | Q5 | Q6 | Q7 | Q4 |
| №3 | - | Q1 | Q2 | Q5 | Q3 | Q6 | Q4 | Q7 |
| №4 | - | Q1 | Q3 | Q2 | Q5 | Q4 | Q6 | Q7 |
| №5 | - | Q3 | Q1 | Q5 | Q2 | Q6 | Q4 | Q7 |
Решение:
Для решения используем формулу:
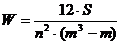 ,
,
W – коэффициент конкордации;
S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;
n – число экспертов;
m – число объектов экспертизы.
0<W<1
При W=0 – полная несогласованность
W=1 – полное единодушие.
Лучше все расчетные данные свести в таблицу
| № объекта экспертизы | Оценка эксперта | сумма рангов | Qср. | Отклонение от среднего | Квадрат отклонения | Сумма квадратов отклонений (S) | 12S | n2 | m3 | m3-m | W | ||||
| 0,85 | |||||||||||||||
| -8 | |||||||||||||||
| -7 |
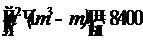 .
.
Ответ: Мнения экспертов достаточно согласованы.
Пример 13
Необходимо определить степень согласованности мнения девяти экспертов.
Результаты мнения экспертов представлены следующим образом.
| №1 | - | Q3 | Q2 | Q1 | Q5 | Q6 | Q4 |
| №2 | - | Q2 | Q3 | Q1 | Q5 | Q4 | Q6 |
| №3 | - | Q3 | Q1 | Q2 | Q6 | Q4 | Q5 |
| №4 | - | Q4 | Q2 | Q3 | Q1 | Q6 | Q5 |
| №5 | - | Q3 | Q1 |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-29 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд