З а д а ч а Д3.П р и м е р 1.
ПРИМЕНЕНИЕ ТЕОРЕМЫОБ ИЗМЕНЕНИИКИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫК ОПРЕДЕЛЕНИЮ СКОРОСТИ И УСКОРЕНИЯ ГРУЗА
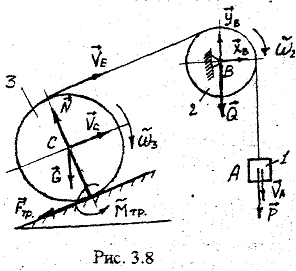
Груз А весом Р при помощи нерастяжимой нити, перекинутой через блок В весом Q и радиусом r, приводит в движение каток весом G и радиусом R. Коэффициент трения качения катка D о плоскость равен k.
Определить скорость и ускорение груза после того, как онопустится на расстояние S. Блок и каток считать однородными цилиндрами. Весом нити и ее проскальзыванием на блоке пренебречь. В начальный момент времени система находилась в покое (рис. 3.8.).
Решение
1. Рассмотрим движение механической системы, состоящей из блока В, груза А, катка D и нити.
2. Внешними силами, действующими на систему (активными), являются силы тяжести груза – Р, блока – Qи катка – G.
3. Внешними силами со стороны связей – гладкого цилиндрического подшипника В и шероховатой деформируемой плоскости – являются для блока: реакции подшипника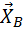 
и 
, а для катка: нормальная составляющая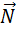 
, сила трения сцепления с поверхностью 
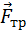и момент пары трения качения 
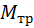, причем во время движения 
.
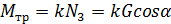4. Определение скорости груза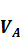 
как функции его перемещения S с помощью теоремы об изменении кинетической энергии системы в конечной форме
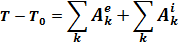
5. Поскольку в начальный момент времени система находилась в покое, начальное значение кинетической энергии равно нулю
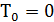. (3.8)
6. Для простоты решения выразим скорости всех тел через скорость груза А. Будем полагать, что нить нерастяжима и не проскальзывает на блоке, тогда все ее точки имеют одинаковую скорость, и модули скоростей точек на ободе блока равны скорости груза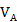 
.
Угловая скорость вращающегося блока будет равна
|
|
.
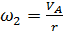На катке, совершающем плоскопараллельное движение, скорость наивысшей точки Ебудет равна скорости груза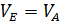 
.
Рассматривая движение точки Е, как вращательное вокруг мгновенного центра скоростей К (точки соприкосновения с неподвижной плоскостью), выражаем угловую скорость катка
.
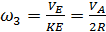Скорость центра катка по формуле вращательного движения вокруг МЦС равна
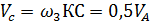
7. Кинетическая энергия системы в конечном (а также промежуточном) положении равна сумме кинетических энергий всех ее подвижных и массивных элементов
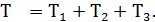
Вид формулы для кинетической энергии каждого тела зависит от характера его движения.
Движение груза А поступательное. Его кинетическая энергия
= 
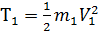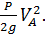
Движение блока вращательное вокруг неподвижной оси, проходящей через его центр масс. Кинетичекая энергия блока
= 
.
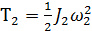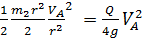Кинетическая энергия однородногокатка, совершающего плоское движение,
= 
.
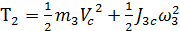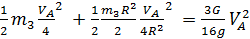В итоге, кинетическая энергия всей системы равна
T=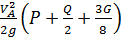 
. (3.9)
8. Замечание. При определении моментов инерции блока и катка считаем их однородными сплошными цилиндрами и определяем моменты инерции относительно оси, проходящей через центр масс, по формулам
9.
.
В случае, когда дляэтих тел вращения заданы радиусы иинерции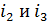 
, формулы для моментов инерции относительно указанных центральных осей имеют вид
.
Сумма работ всех внешних сил
(
) 
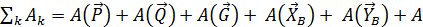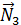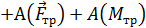
Среди перечисленных слагаемых отличны от нуля лишь три, влияющие на движение системы
,
,
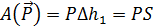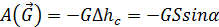а также работа момента сопротивления качению (трения качения)
.
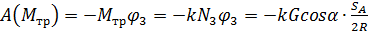Следует отметить, что зависимость между углом поворота катка и перемещением груза такая же как зависимость между угловой скоростью катка и скоростью груза
|
|
, 
.
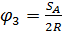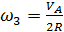Работа остальных сил равна нулю, поскольку они приложены к неподвижным точкам тел, и соответственно, не влияют на движение системы.
Таким образом, суммарная работа внешних сил равна
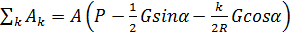(3.10)
Сумма работ внутренних сил равна нулю, так как тела системы твердые, нить нерастяжима и проскальзывание между ними отсутствует.
Теперь, используя выражения (3.7) – (3.10), находим скорость груза А после того, как он переместится на расстояние S
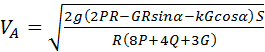. (3.11)
Для нахождения ускорения груза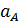 
есть две возможности.
1) Определив зависимость скорости от перемещения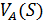 
можно продифференцировать по времени полученное выражение, в котором путь S полагается величиной переменной
.
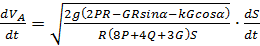С учетом того, что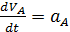 
, 
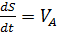и подставляя выражение (3.11), находим
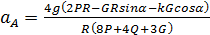(3.12)
2) Вторая возможность найти ускорение – это использовать теорему опроизводной от кинетической энергии системы. Этот путь предпочтительнее, если в задаче не требуется определять скорость, а сразу ставится вопрос об ускорении.
11. Определение ускорения груза с помощью теоремы о производной кинетической энергии по времени
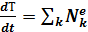(3.13)
Дифференцируя по времени выражение для кинетической энергии (3.9), находим
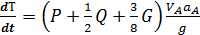. (3.14)
12. Сумма мощностей всех внешних сил равна
.
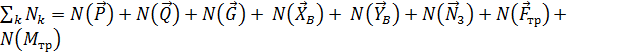Мощности сил 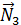и 
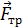, приложенных к точке К, равны нулю, т.к. скорость этой точки равна нулю
.
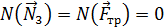Аналогично, к неподвижной точке В приложены и силы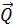 
, 
, 
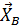, поэтому их мощности также равны нулю
.
|
|
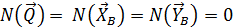Мощности сил тяжест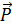и 
и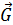 
отличны от нуля и равны
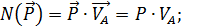(3.15)
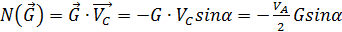. (3.16)
Как видим, мощность движущей силы тяжести груза 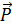положительна, а мощность силы тяжести катка 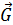, оказывающей сопротивление подъему тела, отрицательна.
Мощность момента пары трения качения всегда отрицательна, т.к. момент направлен противоположно скорости врашения тела
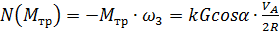. (3.17)
В итоге, сумма мощностей всех внешних сил, влияющих на движение системы, равна
(3.18)
Сумма мощностей всех внутренних сил равна нулю, так как тела системы твердые, нить нерастяжима и проскальзывание между ними отсутствует
Подставляя (3.14) и (3.18) в выражение (3.13), получаем уравнение
,
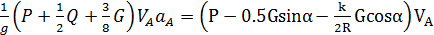откуда находим ускорение груза
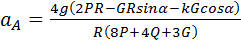. (3.19)
Очевидно, что выражения (3.12) и (3.19) совпалают.
Ответ: скорость груза в конце перемещения S равна
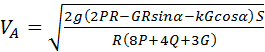
ускорение груза равно
.
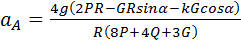