2.1 
Через невесомый блок, укрепленный на ребре призмы, грани которой образуют углы α и β с горизонтом, перекинута нить (рис.). К концам нити прикреплены грузы массами m1 и m2. Найти ускорения грузов и силу натяжения нити. Трением пренебречь.
2.2 На цилиндр массой М намотана нить. Затем цилиндр отпускают, а нить тянут вверх так, что центр массы цилиндра остается при разматывании нити на одной и той же высоте. Чему равна сила натяжения нити?
2.3 
Через легкий вращающийся без трения блок перекинут шнурок. На одном конце шнурка привязан груз массой m1. По другому концу шнура может скользить кольцо о шнурок?
А) С каким ускорением a движется кольцо, если груз массой m1 неподвижен? Чему равна сила трения Fтр кольца о шнурок?
Б) Кольцо соскальзывает с постоянным относительно шнурка ускорением a2. Найти ускорение a1 груза массой m1и силу трения Fтр кольца о шнурок. Груз m1опускается.
2.4 
Система из двух грузов массами m1и m2 (рис.) находится в лифте, движущемся с ускорением a, направленным вверх. Найти силу натяжения Т нити, если коэффициент трения между грузом массой m1и опорой равен k. Изменится ли состояние движения (или покоя) грузов, если направление ускорение лифта изменить на противоположное?
2.5 Шарик всплывает с постоянной скоростью в жидкости, плотность которой в четыре раза больше плотности материала шарика. Определить силу сопротивления жидкости при движении в ней шарика, считая ее постоянной. Масса шарика 10 г.
2.6 Катер массойm = 2 Т трогается с места и в течение времени τ = 10 с развивает при движении по спокойной воде скоростьv = 4 м/с. Определить силу тягиF мотора, считая ее постоянной. Принять силу сопротивленияFc движению пропорциональной скорости, коэффициент сопротивления k = 100 кг/с.
|
|
2.7 Парашютист, масса которогоm = 80 кг, совершает затяжной прыжок. Считая, что сила сопротивления воздуха пропорциональная скорости, определить, через какой промежуток времени τ скорость движения парашютиста будет равна 0,9 от скорости установившегося движения. Коэффициент сопротивления k = 10 кг/с. Начальная скорость парашютиста равна нулю.
2.8 Акробат на мотоцикле описывает «мертвую петлю» радиусомr = 4 м. С какой наименьшей скоростьюvmin должен проезжать акробат верхнюю точку петли, чтобы не сорваться?
2.9 За какое время tтело соскользнёт с наклонной плоскости высотой h, наклоненной под углом α к горизонту, если по наклонной плоскости с углом наклона β оно движется равномерно?
2.10 Сосуд с жидкостью вращается с частотойn = 2 с-1 вокруг вертикальной оси. Поверхность жидкости имеет вид воронки. Чему равен угол φ наклона поверхности жидкости в точках, лежащих на расстоянииr = 5 см от оси?
2.11 Тонкое однородное медное кольцо радиусомR= 10 см вращается относительно оси, проходящей через центр кольца с угловой скоростью ω= 10 рад/с. Определить нормальное напряжение σ, возникающее в кольце, если ось вращения перпендикулярна плоскости кольца.
2.12 
Тележка массой М может катиться без трения по горизонтальному пути. У заднего края тележки лежит брусок массой m. Коэффициент трения между бруском и тележкой k. К бруску приложена горизонтальная сила F, достаточная для того, чтобы брусок начал скользить. Через какое время t брусок упадет с тележки, если длина ее l(рис.)? При какой минимальной силе F0 брусок начнет скользить?
|
|
2.13 
Однородную тонкую пластину ABDK массы m, подвесили за углы А и В на двух невесомых нитях АМ и BN (рис.) так, что ее ость симметрии AF расположена горизонтально. Пренебрегая массой нитей, найдите силу натяжения Т нити BN, если h=6h1.
2.14 Диск радиусом Rи превоначальной массой М подвешен, как показано на рисунке. Определите силы натяжения нитей.
2.15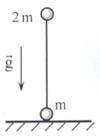 
На гладкую горизонтальную поверхность поставили вертикально гантельнку(рис.) длины l, состоящую их невесомого жесткого стержня с двумя маленькими шариками на концах, массы которых 2m и m. Гантельку отпускают без начальной скорости и она начинает падать. Найдите скорость, с которой верхний шарик коснется горизонтальной поверхности, и величину перемещения нижнего шарика к этому моменту времени. Трением пренебречь.
2.16 
Груз 1 массы m подвешен через пружину жёсткости k на нерастяжимой нити, перекинутой через блок, соединённой с бруском 2, лежащим на горизонтальной плоскости. В начальный момент груз m удерживается так, что пружина находится в ненапряженном состоянии, затем его отпускают без начальной скорости. Найдите минимальную массу бруска 2, при которой он ещё будет оставаться неподвижным. Коэффициент трения между бруском 2 и плоскостью равен µ. Массой пружины, нити, блока и трением в нём пренебречь.