Статика. Механические колебания.

5.1 Фонарь массой М=10 кг подвешен над серединой улицы шириной l= 10 м на канате, допустимая сила натяжения которого T= 500 Н. Определить высоту Н крепления концов каната, если точка крепления фонаря должна находиться на высоте h= 5 м.

5.2 Катушка ниток находится на столе (рис.). В какую сторону она будет двигаться, если нить натягивается силой F₁, F₂, F₃(продолжение линии действия силы F₂проходит через точку, лежащую на линии соприкосновения катушки со столом)?

5.3 Стержень АВ, шарнирно закрепленный в точке А, опирается концом В на платформу (рис.). Какую минимальную силу F нужно приложить для того, чтобы сдвинуть платформу с места? Масса стержня m, коэффициент трения стержня о платформу k и угол, образуемый стержнем с вертикалью, равен α. Трением качения колес платформы и трением в остях пренебречь.

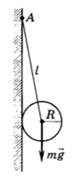
5.4 К вертикальной гладкой стене в точке А на веревке длиной l подвешен шар массой m(рис.). Какова сила натяжения Т веревки и сила давления F шара на стену, если его радиус равен R? Трением о стену пренебречь.

5.5 Железный прут массой М изогнут пополам так, что его части образуют прямой угол (рис.). Прут подвешен за один из концов на шарнире. Найти угол α, который образует с вертикалью верхняя часть стержня в положении равновесия.

5.6 Однородная балка массой М и длиной l подвешена за концы на двух пружинах (рис.). Обе пружины в нерастянутом состоянии имеют одинаковую длину, но жесткость левой пружины в n раз больше. На каком расстоянии x от левого конца балки надо подвесить груз массой m, чтобы она приняла горизонтальное положение. n=2

5.7 Тяжелый брусок удерживается силой трения между двумя стержнями А и В, расположенными горизонтально (рис.). Какими должно быть расстояние x от центра тяжести бруска до точки соприкосновения со стержнем А, чтобы он мог выскользнуть из своих опор? Расстояние a, угол α и коэффициент трения k заданы.

5.8 Найти уравнение гармонических колебаний, если амплитуда колебаний 4 см, период – 0,01 с, а x₀ = 0.

5.9 Изменится ли период колебания маятника от того, что мы поместим его в воду? Маятнику придана идеально обтекаемая форма, и можно принять, что трение о воду равно нулю.

5.10 В неподвижном лифте подвешен маятник, период колебаний которого Т= 1 с. С каким ускорением движется лифт, если период колебаний этого маятника стал равным T₁=1,1 с? В каком направлении движется лифт?

5.11 Найти период колебаний Т математического маятника длиной l, подвешенного в вагоне, движущимся с ускорением a.

5.12 Однородный стержень (рис.) опирается о вертикальную плоскость, образуя с горизонтальной плоскостью угол α= 30^о. Коэффициент трения между стержнем и горизонтальной плоскостью µ₁=0,5. Чему равна минимальная величина коэффициента трения µ₂ между стержнем и вертикальной плоскостью, при которой стержень будет находиться в равновесии?

5.13 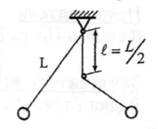Математический маятник (рис.) длины L совершает колебания вблизи вертикальной стенки. Под точкой подвеса маятника на расстоянии l=L/2 от нее в стенку забили гвоздь. Найдите период Т колебаний маятника.

5.14 На подставке лежит тело массы m (рис.), подвешенное на пружине жестокости k. В начальный момент пружина не растянута. Подставку начинают опускать вниз с ускорением a. Через какое время подставка оторвется от тела? Каким будет максимальное растяжение пружины?

5.15 Однородный стержень длины L и массы m шарнирно закреплён в точке О. В точке С, отстоящей на 2L/3 от оси О, стержень опирается на пружину. На стержне закреплены два маленьких груза, массы которых 3m и m, а их положения показаны на рисунке. Найдите силу реакции в шарнире и силу упругости, возникающую в пружине в положении равновесия стержня, когда он неподвижен и расположен горизонтально. Массой пружины и силами трения пренебречь.