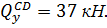УКАЗАНИЯ О ПОРЯДКЕ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
Каждый студент заочной формы подготовки специальности САТ, выполняет две (2) контрольные работы, которые предусмотрены учебным графиком. Задачи, входящие в состав контрольных работ, указаны в таблице №1.
Таблица 1. Состав контрольных работ
| Номер контрольной работы | Номер задачи | Тема задачи |
| Центральное растяжение-сжатие | ||
| Кручение | ||
| Изгиб | ||
| Совместное действие изгиба с кручением | ||
| Устойчивость |
Студент обязан взять из таблицы, прилагаемой к условию задачи, данные в соответствии со своим номером зачётной книжки и первыми шестью буквами русского алфавита, которые следует расположить под шифром, например:
| Номер зачётной книжки 07-3.244 | ||||||
| буквы | а | б | в | г | д | е |
Не следует приступать к выполнению контрольных заданий, не изучив соответствующего раздела курса. Если основные положения теории усвоены слабо и студент обратил мало внимания на подробно разобранные в курсе примеры, то при выполнении контрольных работ возникнут большие затруднения. Несамостоятельно выполненное задание не даёт возможности преподавателю рецензенту вовремя заметить недостатки в работе студента-заочника. В результате студент не приобретает необходимых знаний и оказывается неподготовленным к экзамену.
Тема 1. Основные понятия
В этой теме даны основные понятия, которые необходимо хорошо усвоить. Особое внимание надо обратить на понятия деформаций и напряжений. Для определения напряжений пользуются методом сечений. Сущность его заключается в том, что твердое тело, находящееся в равновесии, разрезают (мысленно) на две части, отбрасывают одну из частей, заменяют влияние отброшенной части внутренними силами и составляют уравнения равновесия для оставшейся части, на которую действуют приложенные к ней внешние и внутренние силы, распределенные по сделанному сечению.
Вопросы для самопроверки. 1. Какие деформации называются упругими? остаточными (пластическими)? 2. Что называется напряжением в точке в данном сечении? 3. Какое напряжение называется нормальным? 4. Какое напряжение называется касательным? 5. В чем сущность метода сечений?
Тема 2. Растяжение и сжатие
В этой теме рассмотрены простые случаи воздействия сил на стержень и содержится ряд вопросов (механические свойства материалов, выбор допускаемых напряжений, статически неопределимые задачи), встречающихся в других разделах курса.
Необходимо обратить внимание на то, что механические характеристики материала (предел пропорциональности, предел упругости, предел текучести, предел прочности) находят путем деления соответствующей нагрузки на первоначальную площадь поперечного сечения. В связи с этим получают условные напряжения, а не истинные; для вычисления последних надо делить нагрузки на действительную площадь поперечного сечения, которая изменяется при опыте. Зная истинные напряжения, можно построить так называемую истинную диаграмму растяжения, которая точнее характеризует свойства материала, чем условная диаграмма. Пользуясь формулами, основанными на законе Гука, надо всегда помнить, что этот закон справедлив только до предела пропорциональности.
Следует обратить внимание на весьма важные понятия: предел прочности, допускаемое напряжение и коэффициент запаса прочности.
После изучения второй темы можно решать задачу 1.
Вопросы для самопроверки. 1. Как строится диаграмма растяжения? 2. Что называется пределом пропорциональности? 3. Что называется пределом упругости, пределом текучести, пределом прочности? 4. Как формулируется закон Гука? 5. Что называется модулем упругости? 6. Что называется коэффициентом поперечной деформации?
Что называется удельной работой деформации? 9. Что называется истинным пределом прочности? 10. В чем заключается разница между пластичными и хрупкими материалами? 11. В каких местах возникает концентрация напряжений? 12. Как находят удлинение стержня, растягиваемого собственным весом? 13. От каких факторов зависит коэффициент запаса прочности? 14. Как формулируется условие прочности?
Тема 3. Кручение
В случае центрального растяжения-сжатия нормальные напряжения распределяются в поперечном сечении стержня равномерно. При расчете на срез обычно считают, что касательные напряжения также распределяются равномерно. В случае кручения круглого стержня касательные напряжения в поперечном сечении распределяются неравномерно, изменяясь по линейному закону — от нуля на оси до максимального значения у поверхности стержня. В связи с этим и возникла мысль о замене сплошного вала полым, материал сечения которого находится в более напряженной зоне и используется рациональнее.
Следует внимательно разобрать построение эпюры крутящих моментов Мк, которая наглядно показывает изменение крутящего момента по длине вала. При вычислении напряжений в каком-либо поперечном сечении вала необходимо брать по эпюре Мк значение соответствующей ординаты.
Надо обратить внимание на то, как используется закон парности касательных напряжений для установления направления τ в точках контура прямоугольного поперечного сечения стержня. Наибольшие напряжения в таком сечении возникают в точках контура, ближе всего расположенных к оси кручения.
После изучения этой темы можно решать задачу 2.
Вопросы для самопроверки. 1. Какие напряжения возникают в поперечном сечении круглого стержня при кручении? 2. Как находят их величину в произвольной точке поперечного сечения? 3. Возникают ли при кручении нормальные напряжения? 4. Чему равен полярный момент инерции круглого сечения? 5. Что называется моментом сопротивления при кручении? 6. Чему равен момент сопротивления кольцевого сечения? Почему нельзя сказать, что он равен разности моментов сопротивления наружного и внутреннего кругов? 7. Как вычисляют момент, передаваемый шкивом, по мощности и числу оборотов? 8. Как находят угол закручивания? 9. Как производят расчет вала на прочность? на жесткость? 10. Как находят максимальные напряжения при кручении стержня прямоугольного сечения? 11. Как вычисляют напряжения в пружинах? 12. Как определяют деформации пружин?
Тема 4. Геометрические характеристики плоских сечений
В теории изгиба важную роль играют моменты инерции, поэтому следует рассмотреть этот вопрос предварительно в виде самостоятельной темы.
Необходимо запомнить, что теорема о переносе осей справедлива только в том случае, если ось у проходит через центр тяжести фигуры. Если, например, известен момент инерции треугольника относительно оси, проходящей через основание, то нельзя при помощи теоремы о переносе осей сразу найти момент инерции треугольника относительно оси, проходящей через вершину параллельно основанию; сначала необходимо при помощи этой теоремы найти момент инерции относительно центральной оси, а затем определить момент инерции относительно оси, проходящей через вершину. Формула переноса осей наглядно показывает, что наименьшим из моментов инерции относительно нескольких параллельных осей является момент инерции относительно той оси, которая проходит через центр тяжести.
Наименьшим из моментов инерции относительно центральных осей, наклоненных под разными углами, является момент инерции относительно одной из главных центральных осей. Относительно другой главной оси, перпендикулярной к первой, момент инерции имеет, наоборот, наибольшее значение. Центробежный момент инерции относительно главных осей равен нулю; при этом совсем не обязательно, чтобы главные оси проходили через центр тяжести, так как через любую точку, лежащую в плоскости фигуры, можно провести такие две взаимно перпендикулярные оси, относительно которых центробежный момент инерции будет равен нулю. В теории изгиба весьма важную роль играют главные центральные оси, положение которых для несимметричных сечений определяют так:
1) сначала проводят случайные оси, вычисляют статические моменты сечения относительно этих осей (разделив предварительно сложную фигуру на ряд простых фигур) и находят положение центра тяжести сечения;
2) проводят через центр тяжести всего сечения оси, параллельные первоначально выбранным случайным осям, и находят при помощи теоремы о переносе осей центробежный и осевые моменты инерции сечения относительно этих новых осей;
3) находят положение главных центральных осей U и V по формуле tg2α0= 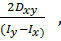
4) находят главные центральные моменты инерции. Для проверки правильности вычислений Iuи Iv можно использовать равенства: Iu+ Iv = Ix + Iy и Dxy= 0.
Следует иметь в виду, что соблюдение этих равенств не гарантирует правильности вычислений.
При пользовании формулой поворота осей надо обязательно обратить внимание на знак угла α: если для совмещения оси х0 с осью х надо повернуть ось х0 по часовой стрелке, то угол α следует считать отрицательным.
После изучения этой темы можно решать задачу 3.
Вопросы для самопроверки. 1. По каким формулам находят координаты центра тяжести плоской фигуры? 2. Чему равна сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей? 3. Какие оси называются главными? 4. Для каких фигур можно без вычислений установить положение главных центральных осей? 5. Относительно каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения? 6. Какой из двух моментов инерции треугольника больше: относительно оси, проходящий через основание, или относительно оси, проходящей через вершину параллельно основанию? 7. Какой из двух моментов инерции квадратного сечения больше: относительно центральной оси, проходящей параллельно сторонам, или относительно оси, проходящей через диагональ? 8. Какой из двух главных центральных моментов инерции полукруглого сечения больше: относительно оси, параллельной диаметру, ограничивающему сечение, или относительно перпендикулярной оси?
Тема 7. Изгиб прямых брусьев
Эта тема является самой большой и самой сложной темой курса сопротивления материалов; ее следует изучать постепенно, обращая особое внимание на решение задач. Сначала надо усвоить весьма важные понятия изгибающего момента М и поперечной силы Q и научиться свободно строить эпюры М и Q.
Необходимо помнить, что поперечная сила в данном сечении равна алгебраической сумме проекций сил, расположенных только по одну сторону от рассматриваемого сечения, на перпендикуляр к оси балки, а изгибающий момент в данном сечении равен алгебраической сумме моментов сил, расположенных только с одной стороны, относительно центральной оси поперечного сечения. В связи с этим рекомендуется — при вычислениях, например, изгибающего момента в сечении балки как момента левых сил — закрывать чем-либо (рукой, книгой, листом бумаги) часть балки, расположенную правее рассматриваемого сечения, чтобы открытыми оставались только одни левые силы. Следует при этом иметь в виду, что можно рассматривать как одни левые, так и одни правые силы, в зависимости от того, с какой стороны проще получить выражения Q и М.
Весьма важное значение имеет теорема Журавского, устанавливающая зависимость между Q и М, с помощью которой можно проверять построение эпюр.
Необходимо обратить внимание на неравномерность распределения нормальных напряжений по высоте балки и на то, что прочность балки зависит от момента сопротивления W. Надо ясно представлять, каким путем можно увеличить момент сопротивления без увеличения расхода материала.
Рекомендуется сравнить между собой эпюры ơ иτ, построенные для балки прямоугольного поперечного сечения.
После изучения этой темы можно решать задачу 4.
Вопросы для самопроверки. 1. Как находят изгибающий момент в каком-либо сечении балки? 2. В каком случае изгибающий момент считается положительным? 3. Как находят поперечную силу в каком- либо сечении балки? 4. Когда поперечная сила считается положительной? 5. Какая существует зависимость между величинами М и Q? 6. Как находят максимальный изгибающий момент? 7. Какой случай изгиба называется чистым изгибом? 8. По какой кривой изогнется балка в случае чистого изгиба? 9. Как изменяются нормальные напряжения по высоте балки? 10. Что называется нейтральным слоем и где он находится? 11. Что называется моментом сопротивления при изгибе? 12. Как выгоднее положить балку прямоугольного сечения при работе на изгиб: на ребро или плашмя? 13. Какое сечение имеет больший момент сопротивления при одинаковой площади: круглое или квадратное? 14. В каких плоскостях возникают касательные напряжения при изгибе, определяемые по формуле Журавского? Как их находят? 15. Как находят главные напряжения при изгибе? 16. Какие напряжения появятся в балке, если плоскость действия нагрузки не пройдет через центр изгиба? 17. Как пишется общее дифференциальное уравнение изогнутой оси балки? 18. Как находят постоянные интегрирования? 19. Как определяют наибольший прогиб? 20. Что представляют собой члены правой части уравнения трех моментов? 21. Как определяют опорные реакции неразрезной балки? 22. В чем преимущества
Задачи для контрольных работ
Задача 1. Растяжение и сжатие
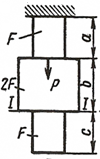
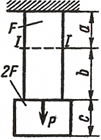
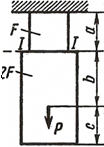
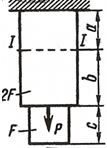
Стальной стержень(Е=2•105 МПа) находится под действием продольной силы Р и собственного веса (γ=78кН/м3). Найти перемещение сечения I-I (рисунок 1) Данные взять из таблицы 1.
Таблица 1. Исходные данные для задачи №1
| Номер строки | Номер схемы | Площадь А, см2 | Расстояния, м | P, H | ||
| a | b | c | ||||
| I | 2,1 | 2,1 | 1,1 | |||
| II | 2,2 | 2,2 | 1,2 | |||
| III | 2,3 | 2,3 | 1,3 | |||
| IV | 2,4 | 2,4 | 1,4 | |||
| V | 2,5 | 2,5 | 1,5 | |||
| VI | 2,6 | 2,6 | 1,6 | |||
| VII | 2,7 | 2,7 | 1,7 | |||
| VIII | 2.8 | 2.8 | 1.8 | |||
| IX | 2.9 | 2.9 | 1.9 | |||
| X | 3.0 | 3.0 | 2.0 | |||
| е | в | г | д | е | г |
 I I
| II
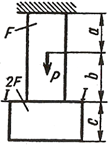
| |
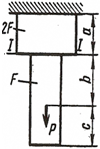
III
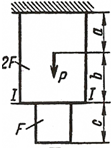
| IV
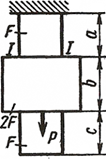
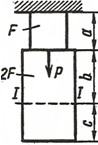
| |
V
| VI
| |
VII

| VIII
| |
 IX IX
|  X X
|
| Рисунок 1.Расчётные схемы к задаче №1 |
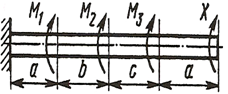
Задача 2. Кручение
К стальному валу приложены три известных момента: М1, М2, М3 (рисунок 2). Требуется: 1) установить, при каком значении момента X угол поворота правого концевого сечения вала равен нулю; 2) для найденного значения X построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов закручивания; 5) найти наибольший относительный угол закручивания (на 1 метр). Данные взять из таблицы 2.
Таблица 2. Исходные данные для задачи №2
| Номер строки | Номер схемы | Расстояния, м | Моменты, Нм | [τ], МПа | ||||
| a | b | c | М1 | М2 | М3 | |||
| I | 1,1 | 1,1 | 1,1 | |||||
| II | 1,2 | 1,2 | 1,2 | |||||
| III | 1,3 | 1,3 | 1,3 | |||||
| IV | 1,4 | 1,4 | 1,4 | |||||
| V | 1,5 | 1,5 | 1,5 | |||||
| VI | 1,6 | 1,6 | 1,6 | |||||
| VII | 1,7 | 1,7 | 1,7 | |||||
| VIII | 1.8 | 1.8 | 1.8 | |||||
| IX | 1.9 | 1.9 | 1.9 | |||||
| X | 2.0 | 2.0 | 2.0 | |||||
| е | г | д | е | г | д | е | в |
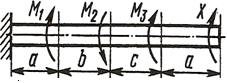  I II I II
|
  III IV III IV
|
  V VI V VI
|
 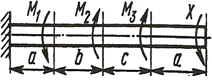 VII VIII VII VIII
|
IX  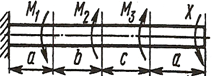 X X
|
| Рисунок 2.Расчётные схемы к задаче №2 |
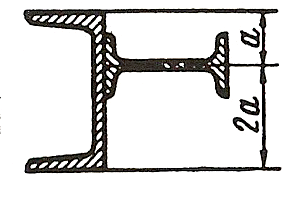
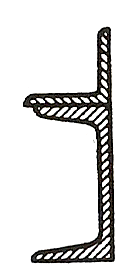
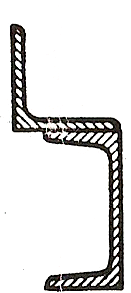
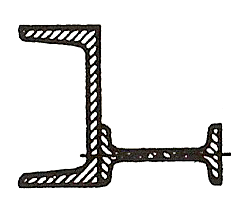
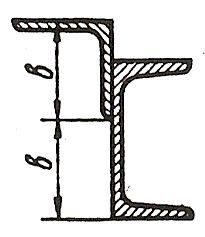
ЗАДАЧА 3. Геометрические характеристики плоских сечений
Для заданного в таблице 3 поперечного сечения, состоящего из швеллера и равнобокого уголка или из двутавра и равнобокого уголка, или из швеллера и двутавра (рисунок 3), требуется: 1) определить положение центра тяжести; 2) найти осевые и центробежный моменты инерции относительно случайных осей, проходящих через центр тяжести (zc и ус); 3) определить направление главных центральных осей (и и v); 4) найти моменты инерции относительно главных центральных осей; 5) вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.
Таблица 3. Исходные данные для задачи №3
| Номер строки | Номер схемы | Швеллер | Равнобокий уголок | Двутавр |
| I | 80×80×8 | |||
| II | 80×80×6 | |||
| III | 90×90×8 | |||
| IV | 90×90×7 | |||
| V | 90×90×6 | |||
| VI | 100×100×8 | |||
| VII | 100×100×10 | |||
| VIII | 100×100×12 | |||
| IX | 125×125×10 | |||
| X | 125×125×12 | |||
| е | г | д | е |
 I I
|  II II
| |
 III III
|  IV IV
| |
 V V
|  VI VI
| |
 VII VII
|  VIII VIII
| |
 IX IX
| 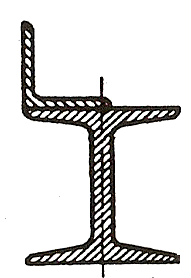 X X
|
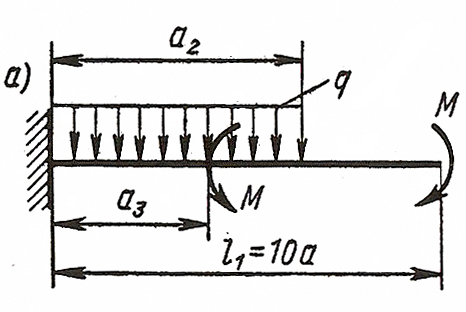
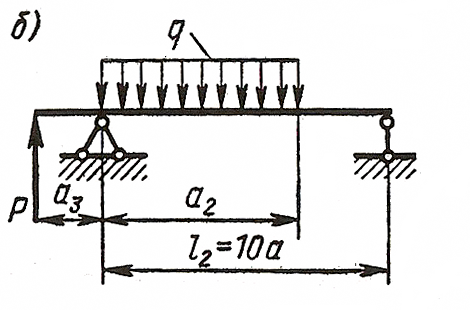
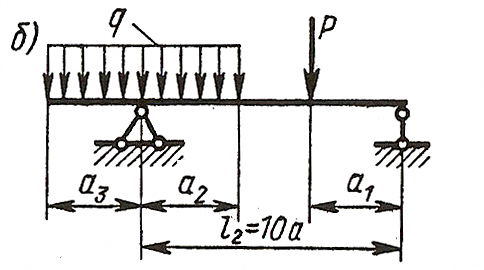
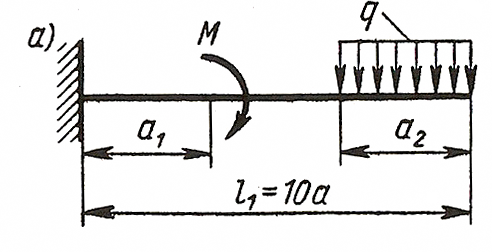
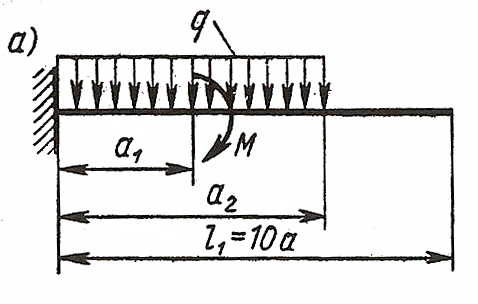
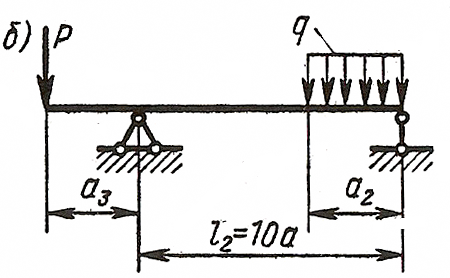
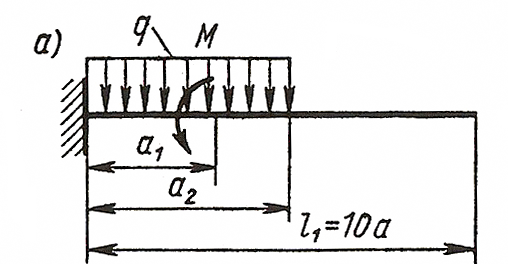
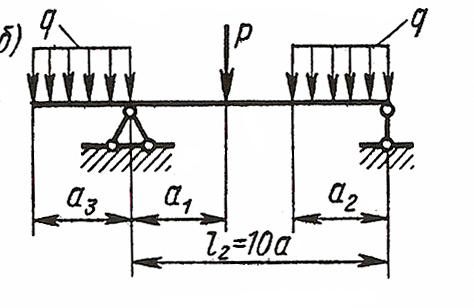
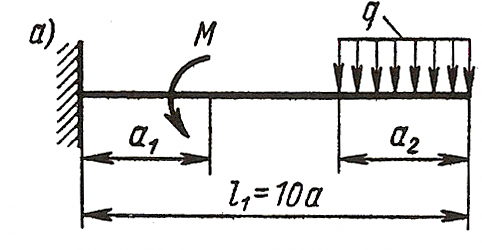
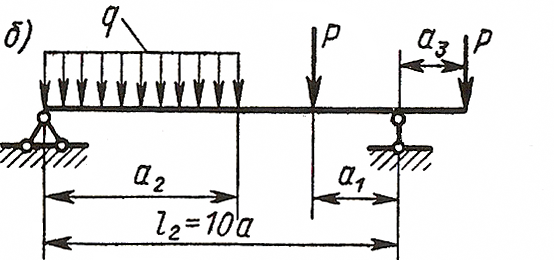
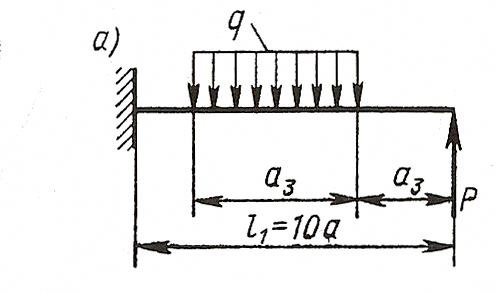
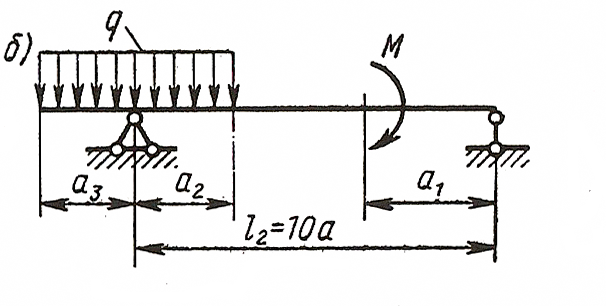
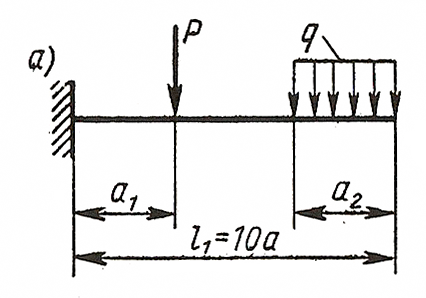
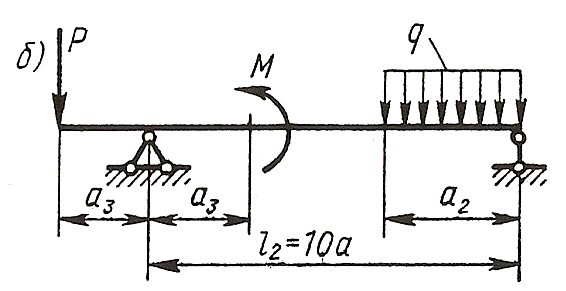
ЗАДАЧА 4. Изгиб прямых брусьев
Длязаданных двух схем балок (рисунок 4) требуется написать
выражения Q и Мизг для каждого участка в общем виде, построить эпюры Q
и Мизг, найти Мmax и подобрать: а) для схемы а деревянную балку
круглого поперечного сечения при [σ] = 8 МПа; б) для схемы б
стальную балку двутаврового поперечного сечения при [σ]= 160 МПа.
Данные взять из таблицы 4.
Таблица 3. Исходные данные для задачи №4
| Номер строки | Номер схемы | l1 | l2 | Расстояния в долях пролёта | M, kHМ | P,kH | q,
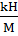
| ||
| м | 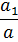
| 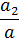
| 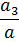
| ||||||
| I | 1,1 | ||||||||
| II | 1,2 | ||||||||
| III | 1,3 | ||||||||
| IV | 1,4 | ||||||||
| V | 1,5 | ||||||||
| VI | 1,6 | ||||||||
| VII | 1,7 | ||||||||
| VIII | 1,8 | ||||||||
| IX | 1,9 | ||||||||
| X | 2,0 | ||||||||
| е | д | е | г | д | е | г | д | е |
I
|
II
|
 II II
|
 IV IV
|
 V V
|
| Рисунок 4.Расчётные схемы к задаче №4 |
  VI VI
|
 VII VII
|
VIII
|
IX
|
  X X
|
Примеры решения задач
Задача №1. Растяжение и сжатие
Стальной стержень (Е=2∙105 МПа) находится под действием продольной силы Р и собственного веса (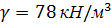 ). Найти перемещение сечений I-I(рисунок).
). Найти перемещение сечений I-I(рисунок).
Исходные данные: схема I, F=20 см2 , а=2.1 см, b=2.8 см, с=2.0 см, Р=1100Н.
Решение 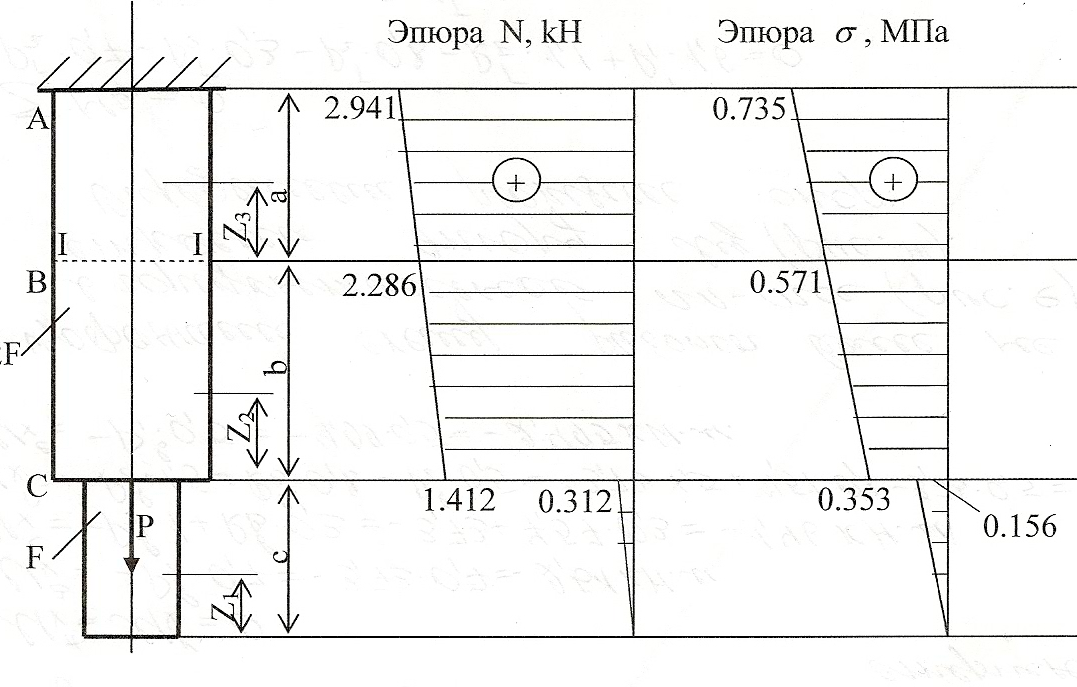
1. Записываем выражение продольной силы для каждого участка и строим эпюру N:
- участок CD, 0≤z1≤2.0 м
N= 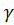 ∙F∙z1 при z1=0 N=0,
∙F∙z1 при z1=0 N=0,
при z1=2.0 м N=0.312 кН,
- участок BC, 0≤z2≤2.8 м
N= 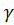 ∙F∙c∙+P+
∙F∙c∙+P+ 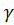 ∙2∙F∙z2 при z2=0 N=1.412 кН,
∙2∙F∙z2 при z2=0 N=1.412 кН,
при z2=2.8 м N=2.286 кН,
- участок AB, 0≤z3≤2.1 м
N= 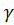 ∙F∙c∙+P+
∙F∙c∙+P+ 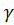 ∙2∙F∙(b+z3) при z3=0 N=2.286 кН,
∙2∙F∙(b+z3) при z3=0 N=2.286 кН,
при z3=2.1 м N=2.941 кН.
2. Находим напряжение на каждом участке стержнях и строим эпюру их распределения по длине стержня:
-участок CD, σD =0 σC =0.156 Мпа;
-участок ВС, σС =0.353 МПа σC =0.571 Мпа;
-участок AB, σB =0.571 МПа σC =0.735 Мпа.
3. Определяем перемещение сечения I-I
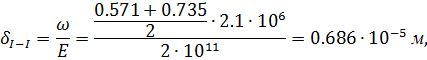
Где ω- площадь эпюры σ на участке AB.
Задача №2. Кручение
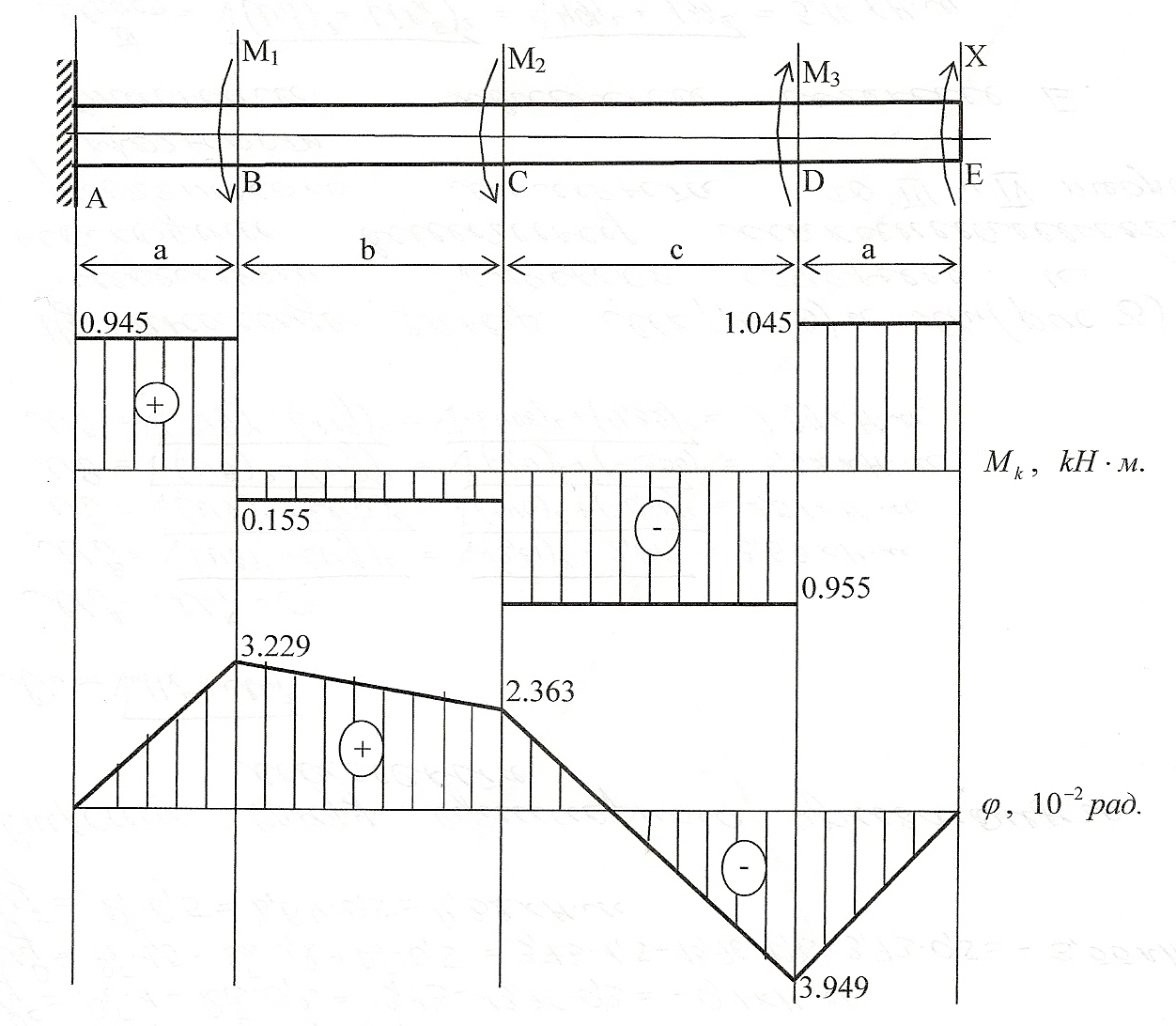
К стальному валу приложены три момента: М1, М2, М3 (рис). Требуется: 1) установить, при каком значении момента Х угол поворота правого концевого сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100мм; 4) построить эпюру углов закручивания; 5) найти наибольший относительный угол закручивания (на 1м).
Дано: схема Х, а=1.1 м, b=1.8 м, c=2.0 м, М1=1.1кНм, М2=0.8кНм, М3=2.0кНм, [τ]=80 Мпа, G=8∙104 Мпа.
Решение
1. Находим, при каком значении момента Х угол поворота правого концевого сечения вала  равен нулю
равен нулю
 (1)
(1)
Запишем значение крутящего момента для каждого участка вала:
-участок DE Mk(DE)=-X
-участок CD Mk(CD)=-X-M3=-X-2.0
-участок BC Mk(BC)=-X-M3+ M2=-X-2.0+0.8=-X-1.2
-участок AB Mk(AB)=-X-M3+ M2+ M1=-X-2.0+0.8+1.1=-X-0.1
Запишем значение углов закручивания на каждом участке вала и подставим их в уравнение(1)
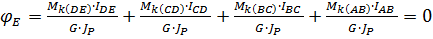 (1’)
(1’)
Сократим уравнение (1’) на знаменатель и подставим значение крутящих моментов длин участков
(-Х-0.1)∙1.1+(-Х-1.2) ∙1.8+(-Х-2.0) ∙2.0+(-Х) ∙1.1=0
-6.0X-6.27=0 X=-1.045кН∙м.
Знак (минус) указывает на то, что направление момента Х на расчетной схеме нужно поменять на противоположное.
2. Определяем значения крутящего момента для каждого участка и строим эпюру крутящих моментов
-участок DE Mk(DE)=-X=1.045 кН∙м,
-участок CD Mk(CD)=- X-2.0=1.045-2.0=-0.955 кН∙м,
-участок BC Mk(BC)=-X-1.2=1.045-1.2=-0.155 кН∙м,
-участок AB Mk(AB)=- X-0.1=1.045-0.1=0.945 кН∙м.
3. При заданном значение [τ]=80 Мпа определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100мм
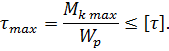
Из условия прочности определяем требуемую величину полярного момента сопротивления
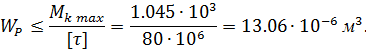
Для круглого поперечного сечения 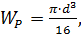 откуда
откуда

Принимаем диаметр вала d=45мм.
4. Строим эпюру углов закручивания. Сечение А защемлено, поэтому 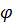 А=0. Найдем значения углов закручивания для других сечений:
А=0. Найдем значения углов закручивания для других сечений:
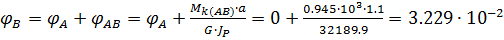 рад,
рад,
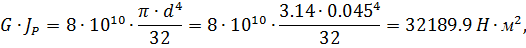
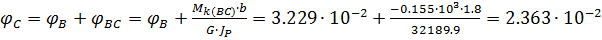 рад,
рад,
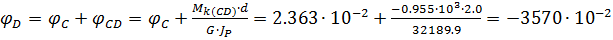 рад,
рад,
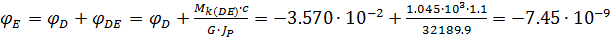 рад.
рад.
5. Определяем наибольший относительный угол закручивания
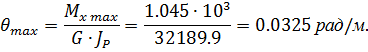
Задача №3. Геометрические характеристики плоских сечений
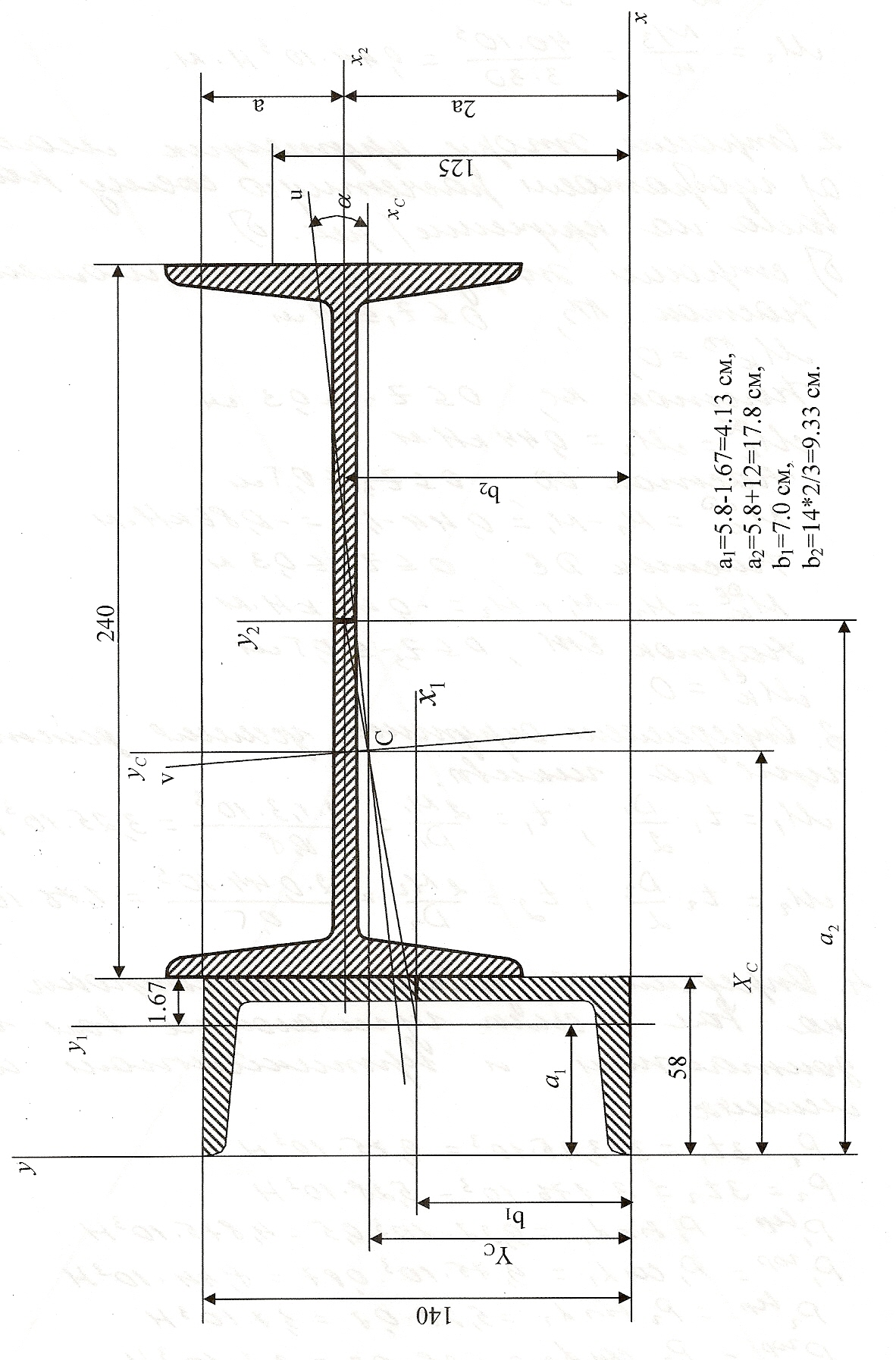
Для заданного поперечного сечения, состоящего из швеллера и равнобокого уголка, или из двутавра и равнобокого уголка, или из швеллера и двутавра (рисунок), требуется: 1) определить положение центра тяжести; 2)найти осевые (экваториальные) и центробежные моменты инерции относительно случайных осей, проходящих через центр тяжести (zc и yc); 4) найти моменты инерции относительно главных центральных осей; 5) вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.
Дано: схема Х, швеллер №14, двутавр №24.
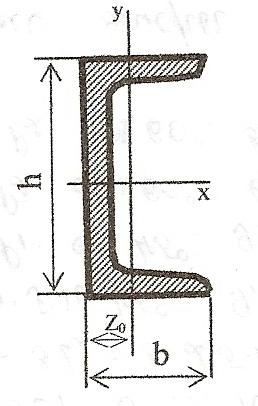 Швеллер №16
Швеллер №16
h=140 мм,
b=58 мм,
А=15.6 см2,
Jx=491 см4,
Jy=45.4 см4,
Z0=1.67 см.
Двутавр №24
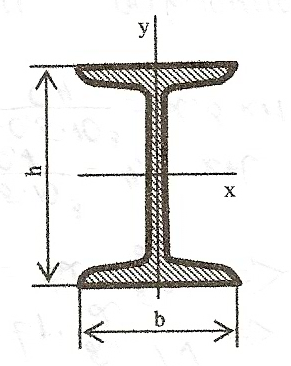 h=240 мм,
h=240 мм,
b=115 мм,
А=34.8 см2,
Jx=3460 см4,
Jy=198 см4.
Решение
1. Определяем положение центра тяжести
а) определяем скммарную площадь сечения
А=А1+А2=15.6+34.8=50.4 см2,
б) определяем статические моменты сечения относительно случайных осей х и у
Sx=A1∙b1+A2∙b2=15.6∙7+34.8∙9.33=434.0 см3,
Sy=A1∙a1+A2∙a2=15.6∙4.13+34.8∙17.8=683.87 см3,
в) определяем координаты центра тяжести
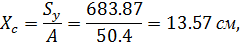
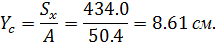
2. Определяем осевые и центробежные моменты инерции относительно случайных центральных осей Xc и Yc
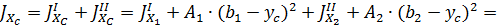
=491+15.6∙(7-8.61)2+198+34.8∙(9.33-8.61)2=747.64 см4
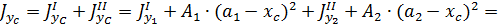
=45.4+15.6∙(4.13-13.57)2+3460+34.8∙(17.8-13.57)2=6420.53 см4,
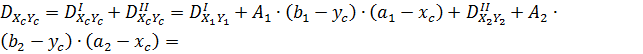 0+15.6∙(7-8.61) ∙(4.13-13.57)+0+34.8∙(9.33-8.61) ∙(17.8-13.57)=343.57 см4.
0+15.6∙(7-8.61) ∙(4.13-13.57)+0+34.8∙(9.33-8.61) ∙(17.8-13.57)=343.57 см4.
3. Определяем направление главных центральных осей u и v
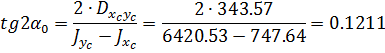
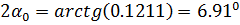
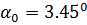
4. Определяем моменты инерции относительно главных центральных осей u и v
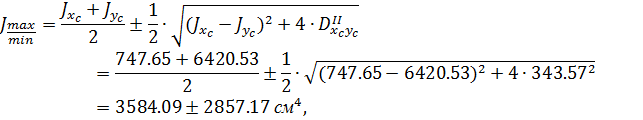
Jmax=Jv=3584.09+2857.17=6441.26 см4,
Jmin=Ju=3584.09-2857.17=726.91 см4.
Задача 4. Изгиб прямых брусьев
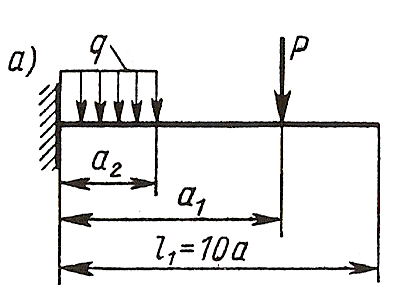
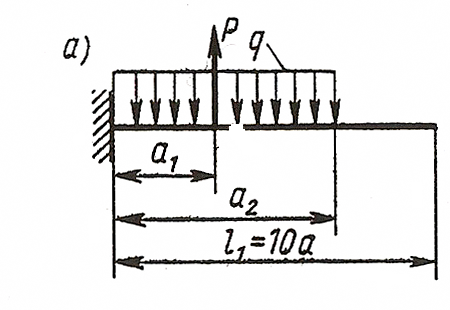
Задача 4а. Для заданных двух схем балок (рисунок) требуется написать выражение Q и M для каждого участка в общем виде, построить эпюры Q и М, найти М мах и подобрать деревянную балку круглого сечения при [σ]=8 Мпа.
Исходные данные: схема Ха, l1=10∙a=1.8 м, а=0.8 м, а1=1∙а=0.18 м, а3=5∙а=0.9 м, Р=9 кН, q=10 kH/м.
Решение
1. Записываем выражение поперечной силы и изгибающего момента для каждого участка и строим эпюры Qy и М.
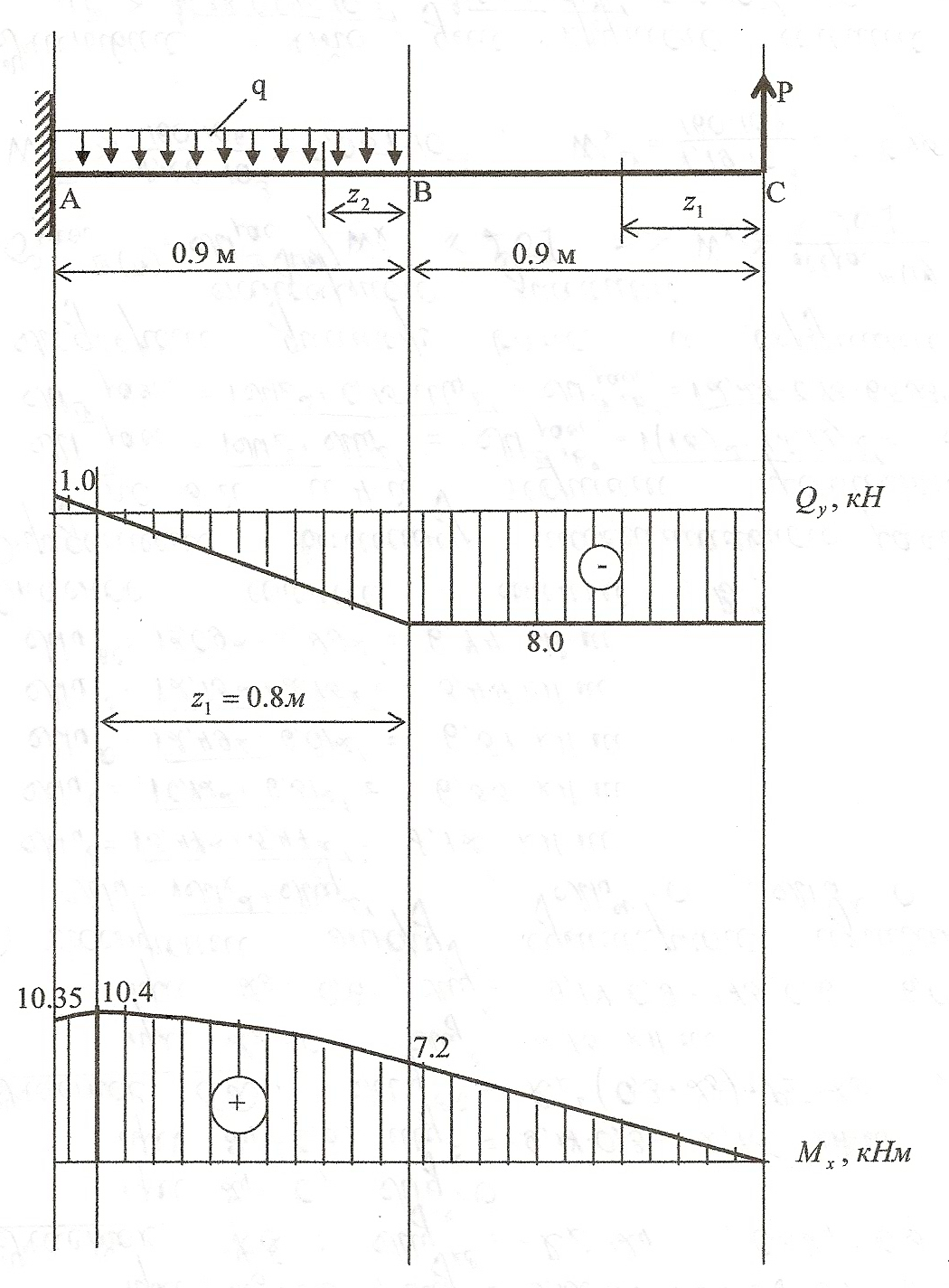
Участок ВС, 0≤z1≤0.9 м
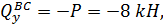
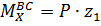 при z1=0
при z1=0 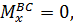
при z1=0.9 м 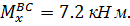
Участок АВ, 0≤z2≤0.9 м
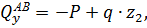
при z2=0 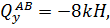
при z2=0.9 м 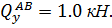
Найдем координаты сечения, в котором поперечная сила 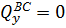
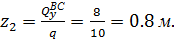
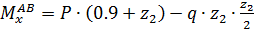 при z2=0
при z2=0 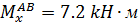
при z2=0.8 м 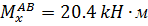
при z2=0.9 м 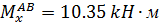
2. Подбираем деревянную балку круглого поперечного сечения при [σ]=8МПа.
Из условия прочности
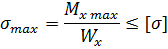
Определяем минимальную величину сопротивления
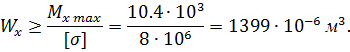
Для круглого поперечного сечения 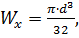 откуда
откуда
 Принимаем d=240 мм.
Принимаем d=240 мм.
Задача №4б. Для заданных двух схем балок (рисунки) требуется написать выражения Q и М для каждого участка в общем виде, построить эпюры Q и М, найти Ммах и подобрать стальную балку двутаврового поперечного сечения при [σ]=160 МПа.
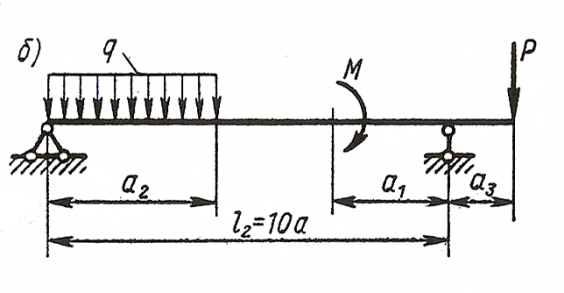
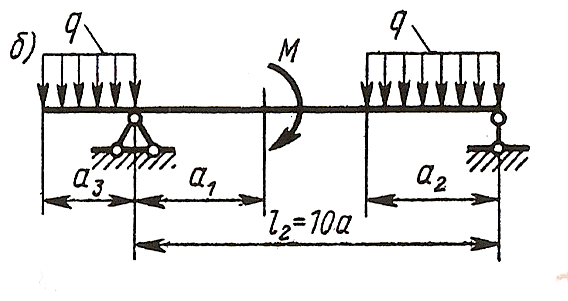
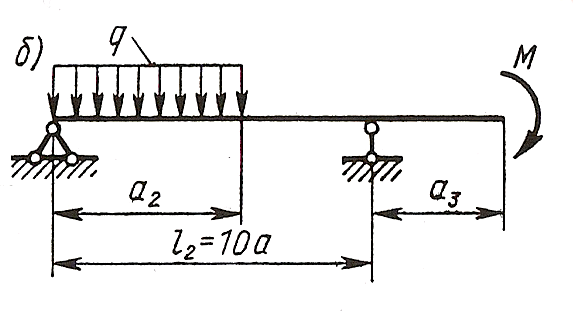
Исходные данные: схема Хб, l2=10-а =10м, а =1.0м, а2=8-а=8.0м, а3=5-а=5.0м, М=10кНм, Р=10 кН, q=8 kH/м.
Решение
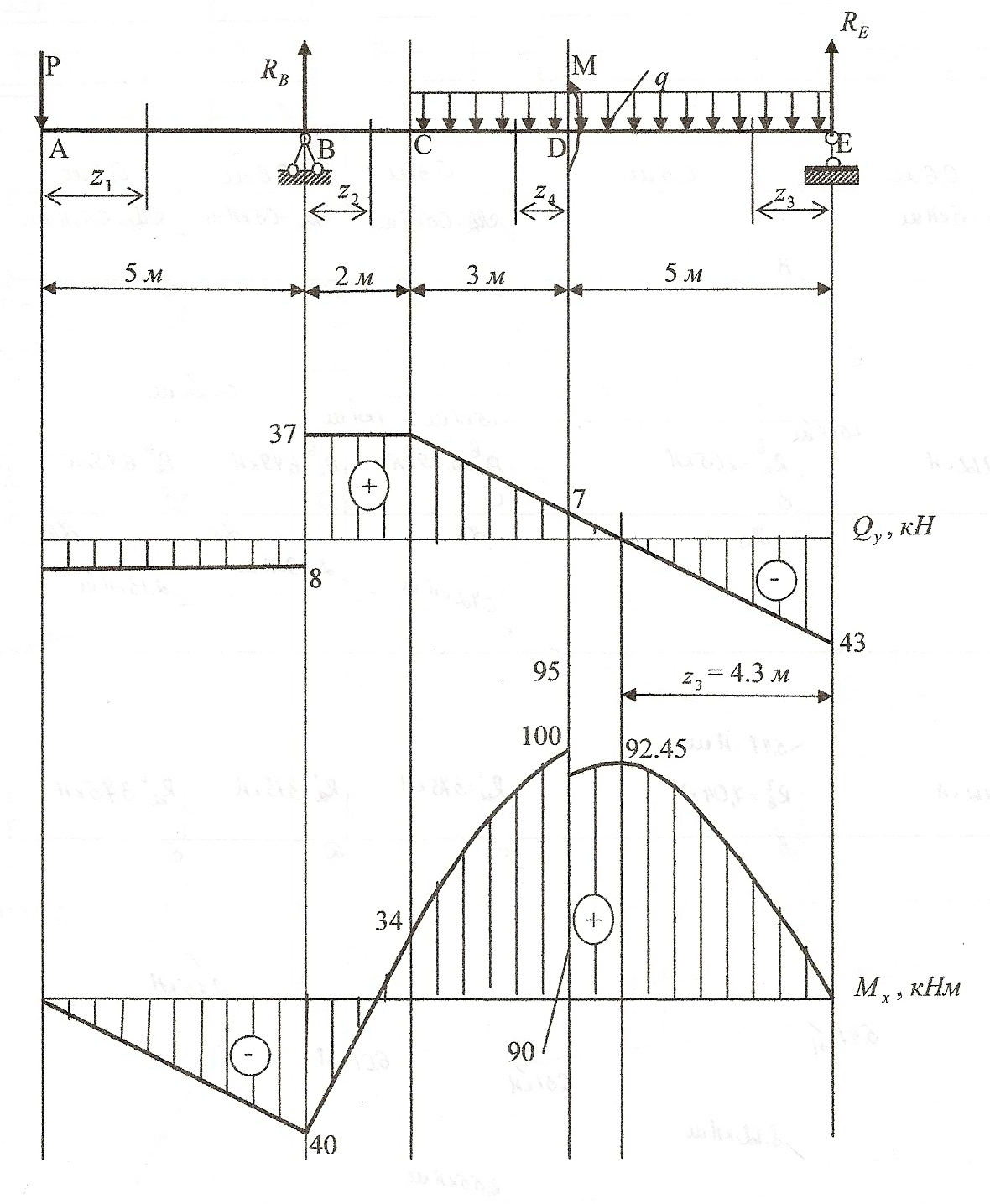
1. Определяем опорные реакции
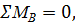
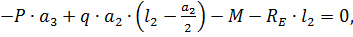
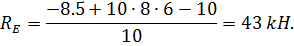
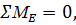
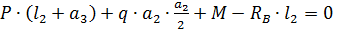
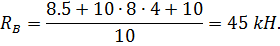
Проверка: 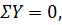
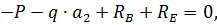
-8-10∙8+45+43=0 88-88=0
2. Записываем выражение поперечной силы и изгибающего момента для каждого участника и строим эпюры Qy и Мx.
Участок AB, 0≤z1≤5 м
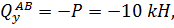
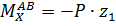 при z1=0
при z1=0 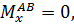
при z1=5 м 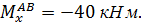
Участок ВС, 0≤z2≤2 м
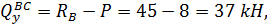
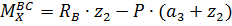 при z2=0
при z2=0 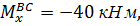
при z2=2 м 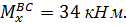
Участок DE, 0≤z3≤2 м
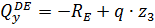 при z3=0
при z3=0 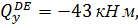
при z3=5 м 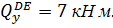
Найдем значение координаты 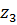 , при которой
, при которой 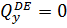
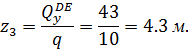
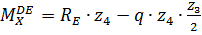 при z3=0
при z3=0 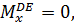
при z3=4.3 м 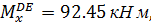
при z3=5 м 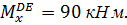
Участок CD, 0≤z4≤3 м
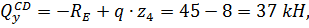 при z4=0
при z4=0 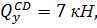
при z4=3 м